Балаковский институт техники, технологии и управления.

Факультет: инженерно – строительный.

Кафедра: управление и информатика в технических системах.

Курсовая работа

по дисциплине

Моделирование систем управления.

Моделирование динамической системы

методом планирования эксперимента.

ВАРИАНТ № 13.

Выполнил: ст.гр. УИТ 52 В

Проверила: доцент кафедры УИТ

Балаково, 2002

содержание

исходные данные ……………………………………………………………………….. введение ……………………………………………………………………………………… ОСНОВНАЯ ЧАСТЬ …………………………………………………………………………… Построение матрицы плана ……………………………………………………………….. Расчет линейной части …………………………………………………………………….. Оценка адекватности модели ……………………………………………………………... Расчет крутого восхождения ………………………………………………………………. ЗАКЛЮЧЕНИЕ …………………………………………………………………………………. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ ………………………………………….

исходные данные

Вариант № 6.

Составить план 2³.

Уровни факторов	Факторы процесса
	Х1	Х2	Х3
Нижний	6	40	0,22
Основной	10	80	0,40
верхний	14	120	0,58

Массив данных.

Y1	Y2	Y3
0,12	0,11	0,12
0,08	0,06	0,08
0,14	0,21	0,20
0,11	0,18	0,18
0,12	0,14	0,14
0,12	1,11	0,11
0,23	0,22	0,21
0,21	0,20	0,18

введение

Цель работы: - изучение метода планирования эксперимента при исследовании многофакторной динамической системы и его применения для получения математиче­ской модели и проверки ее адекватности.

ОСНОВНАЯ ЧАСТЬ

Так как формула для составления плана эксперимента имеет вид 2^k, то, следовательно, мы будем проводить полный факторный эксперимент.

1. Построение матрицы плана.

Составим таблицу уровней факторов и интервалов варьирования.

Факторы	Уровень			Интервал варьирования
	-1	0	+1
X1	6	10	14	4
X2	40	80	120	40
X3	0,22	0,40	0,58	0,36

Для каждого включенного в эксперимент факторов (х₁, х₂, … х_n) устанавливаются только два уровня: x_{j max} и нижний x_{j min}. Основной уровень определяется по формуле:

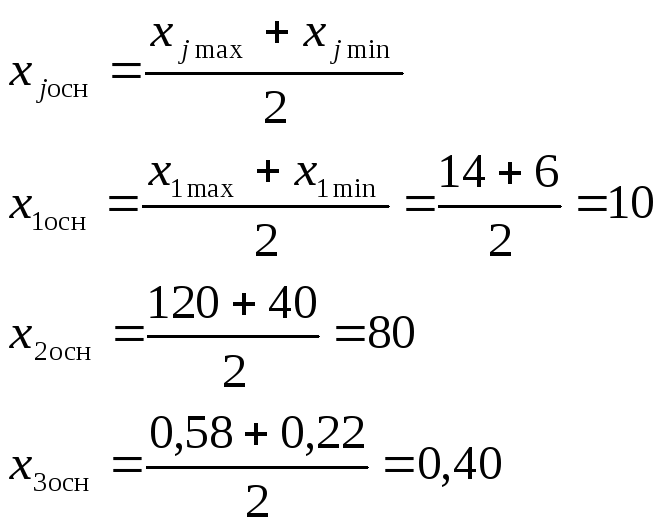
а интервал варьирования по выражению:

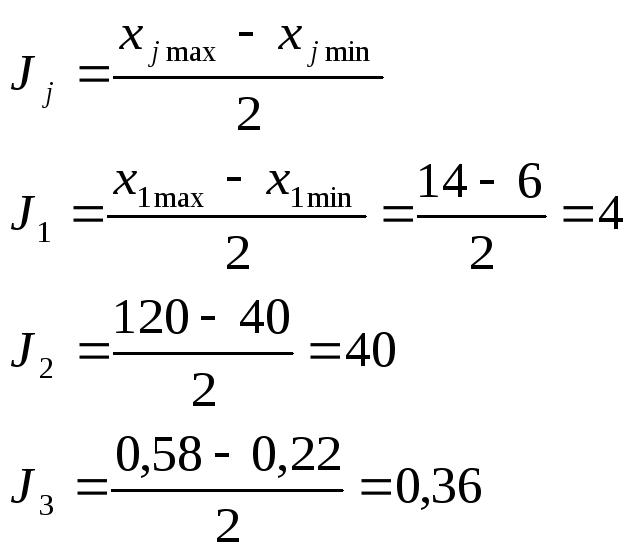
Определим количество опытов:

N = 2³ = 8

1) Составим матрицу планирования для плана 2³.

№№	Факторы			Параметр оптимизации
	Х1	Х2	Х3	Y1	Y2	Y3
1	-	-	-	0,12	0,11	0,12
2	+	-	-	0,08	0,06	0,08
3	-	+	-	0,14	0,21	0,20
4	+	+	-	0,11	0,18	0,18
5	-	-	+	0,12	0,14	0,14
№№	Х1	Х2	Х3	Y1	Y2	Y3
6	+	-	+	0,12	1,11	0,11
7	-	+	+	0,23	0,22	0,21
8	+	+	+	0,21	0,20	0,18

Составленная матрица планирования должна соответствовать свойствам полного факторного эксперимента.

1. Симметричность относительно центра эксперимента:

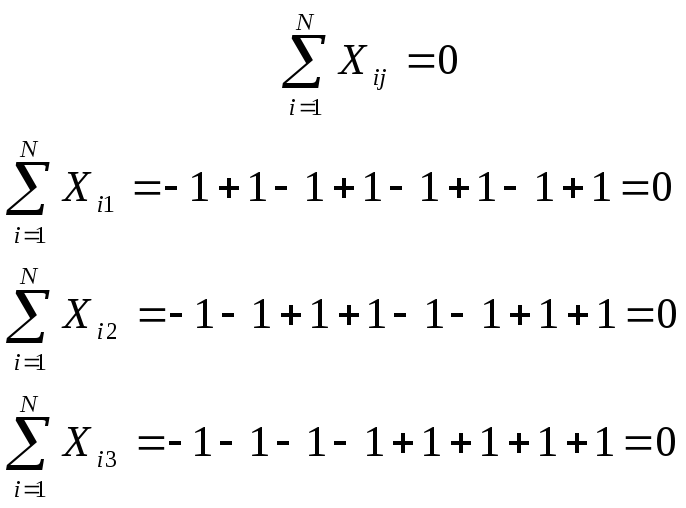
где j – номер фактора; N – число опытов, j = 1 .. k.

2. Условие нормировки:

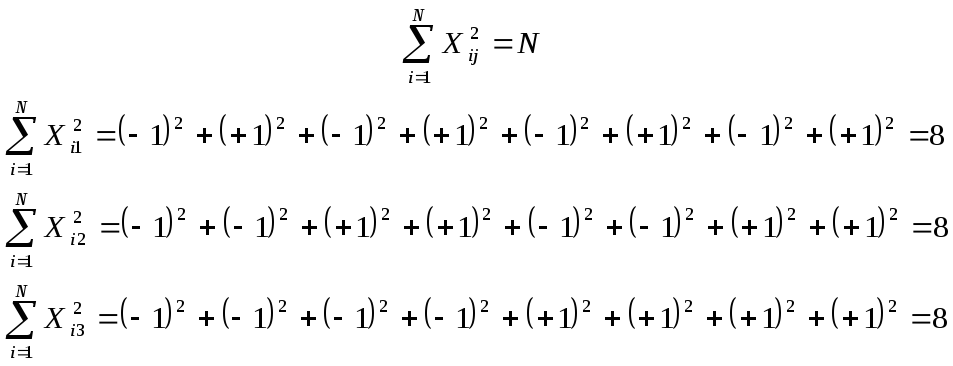
3. Ортогональность матрицы:

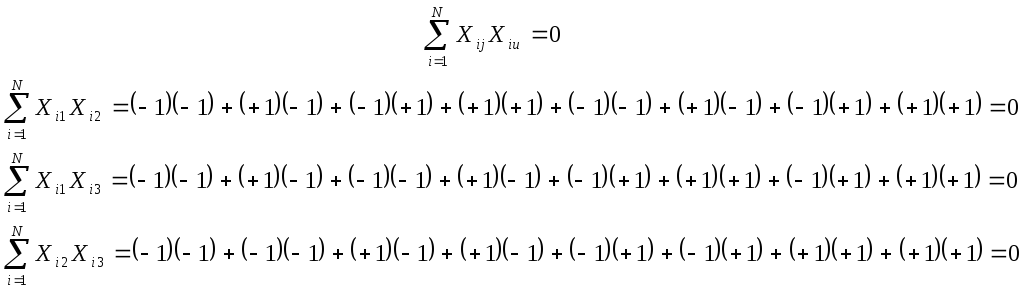
j ≠ u, u = 0, 1, 2, … k.

2. Расчет линейной части.

Записываем уравнение процесса в виде:

Y = b₀ +b₁x₁ + b₂x₂ +b₃x₃

Коэффициент b₀ находится по формуле

Определим среднее значение :

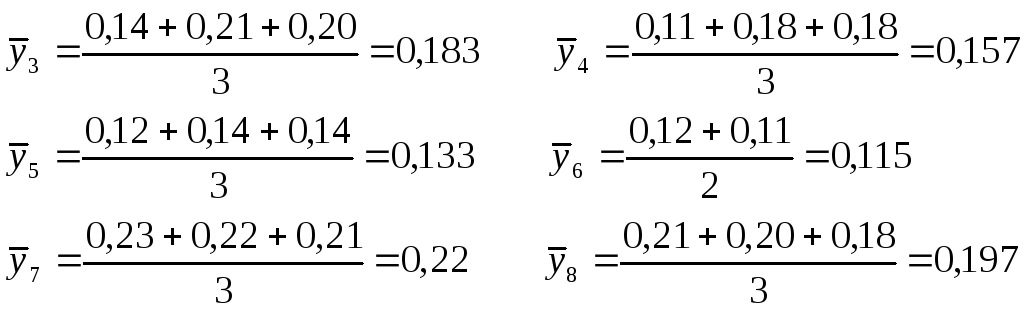
Определим коэффициенты b₀, b₁, b₂, b₃:

С учетом произведенных расчетов линейная модель примет вид:

Y = 0,1494 – 0,0139x₁ + 0,0399x₂ +0,0169x₃

Определим дисперсию:

Проверка на ошибки эксперимента.

Для определения ошибок используем критерий Стьюдента:

так как полученное значение намного больше табличного, то следовательно число 1,11 является промахом и в дальнейших вычислениях учитываться не будет.

Полученные дисперсии проверим на однородность. По критерию Фишера. Для этого берется отношение наибольшей к наименьшей из полученных дисперсий и сравнивается с табличным значением.

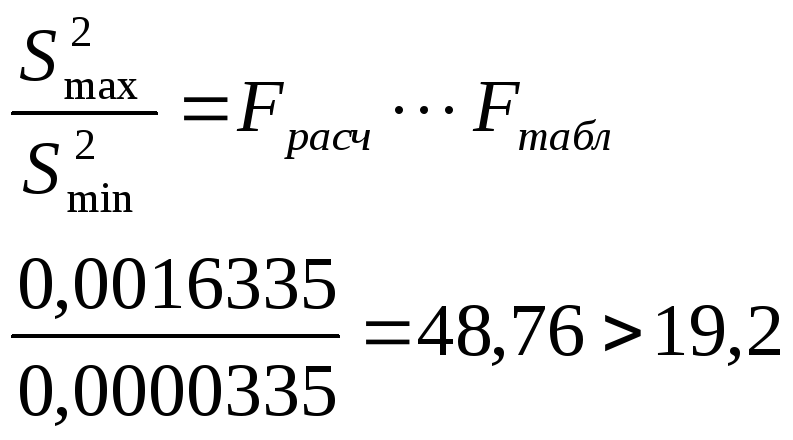
так как расчетное значение больше табличного, то следовательно дисперсия не однородна.

3. Оценка адекватности модели.

№№	Факторы			Параметр оптимизации				S2	f
	Х1	Х2	Х3	Y1	Y2	Y3
1	-	-	-	0,12	0,11	0,12	0,117	0,0000335	2	0,1585
2	+	-	-	0,08	0,06	0,08	0,073	0,0001335	2	0,1863
3	-	+	-	0,14	0,21	0,20	0,183	0,001435	2	0,0787
4	+	+	-	0,11	0,18	0,18	0,157	0,0016335	2	0,1065
5	-	-	+	0,12	0,14	0,14	0,133	0,0001335	2	0,1923
6	+	-	+	0,12	1,11	0,11	0,115	0,00005	1	0,2201
7	-	+	+	0,23	0,22	0,21	0,22	0,0001	2	0,1125
8	+	+	+	0,21	0,20	0,18	0,197	0,0002335	2	0,1403

Дисперсия параметра оптимизации рассчитывается по следующей формуле:

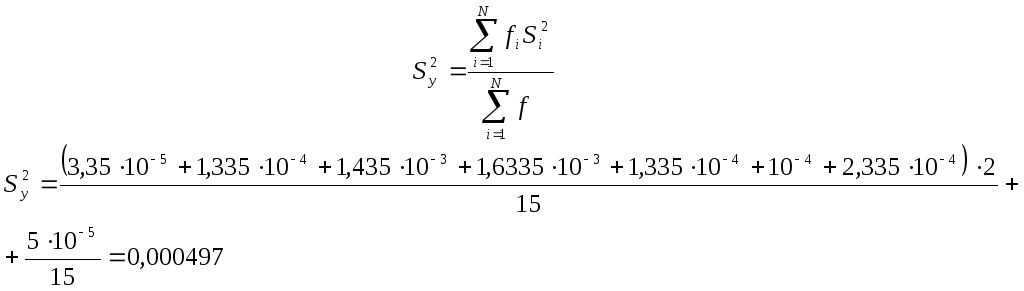
f = N – (k+1) = 8-(3+1) = 4

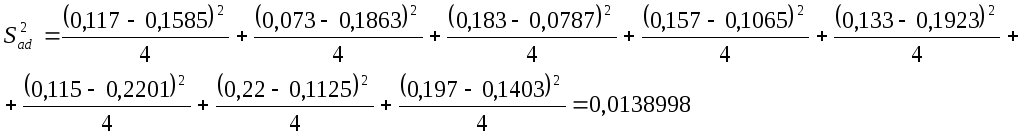
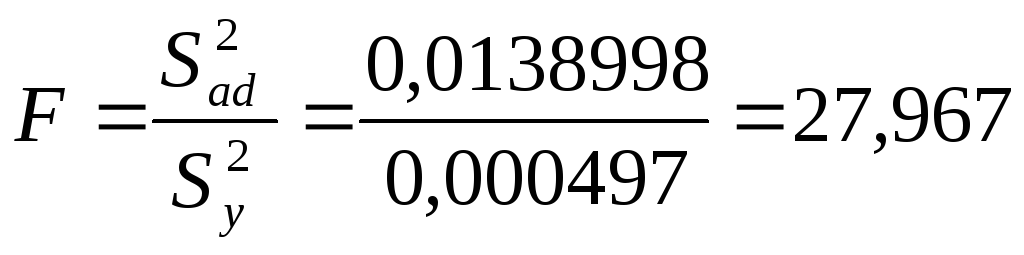
модель не адекватна, что опять где – то лажа, что теперь делать мне это уже начинает надоедать, когда же эта паршивая курсовая доделается, что еще ей не хватает, проверю те значения на ошибки.

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

и при этом получаем следующие результаты

да и дальше то же гарамонд. да это очень будет круто и не только, ха классно

7