4 Синтез интегральной передаточной функции срп

Рассмотрим, как изменяется сопротивление Q платиновой нити 1 при изменении температуры X (рисунок 1).

Исходные данные:

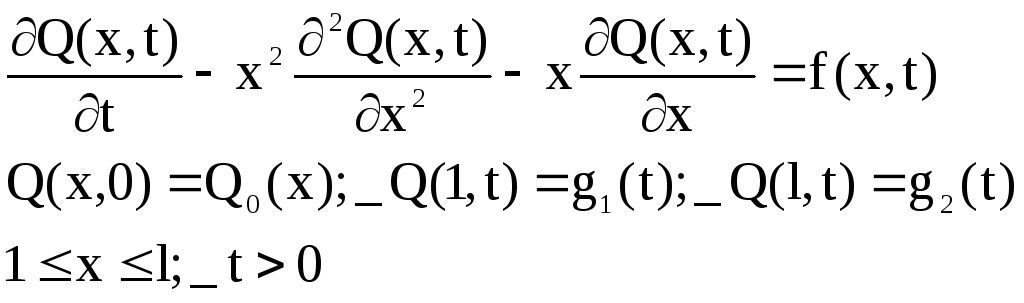
Кроме того:

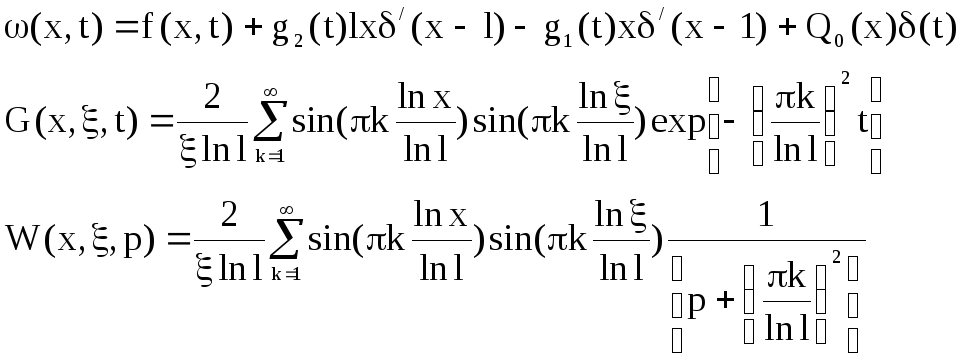
Для начала расчетов проведем идентификацию всех присутствующих величин. Входным возмущением f(x, t) является поток тепла от корпуса металлического терморезистора, который при некотором пренебрежении временем равен потоку тепла от источника тепла, приложенного к нити в точке 0, зададим его в качестве гармонического сигнала: f(x, t)=A*cos(ωt). Сразу зададим коэффициенты входного воздействия. Ограничим температуру значением 100⁰С, частоту изменения входного воздействия примем равной 314 Гц.

Координата точки ξ, в которой нужно найти значение выходной величины как функции от возмущения и 0≤ξ≤l. Введем ограничение на длину нити 8 сантиметрами.

Q – выходная величина, соответствующая сопротивлению нити после воздействия на него теплового потока.

Начальные условия запишутся в виде Q(x,0)=Q₀(x)=4300, что соответствует сопротивлению проводника при 20⁰С.

Граничные условия имеют вид:

Q(1,t)=g₁(t)=4300*(1+5.49*10^-3*100*cos(314*t)+6.66*10^-6(100*cos(314* *t))²)=4300+2361*cos(314*t)+286.38*cos²(314*t)

Q(l,t)=g₂(t)=4300*(1+5.49*10^-3*100*cos(314*t+50)+6.66*10^-6(100* *cos(314*t+50))²)=4300+2361*cos(314*t+50)+286.38*cos²(314*t+50)

Все дополнительные данные взяты из теоретической части.

Выходная величина запишется в виде:

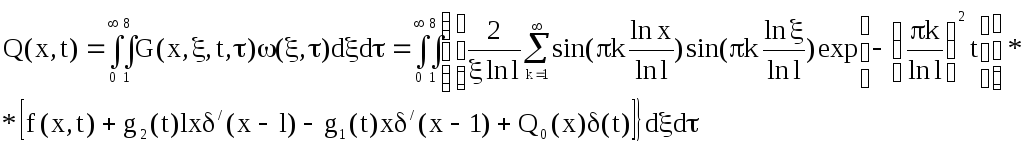
Таким образом, стандартизирующая функция запишется как:

Для определения интегральной передаточной функции необходимо найти операторное выражение выходной величины.

Континуальная передаточная функция примет вид:

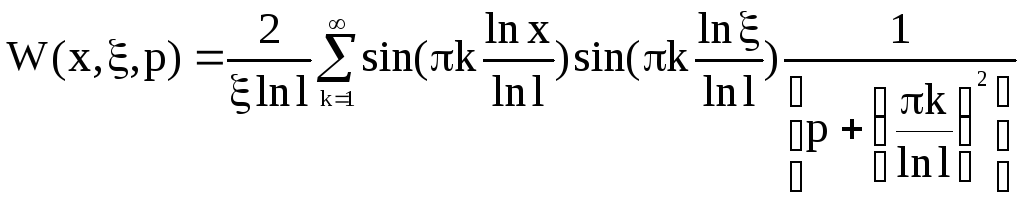
С соблюдением наложенных ограничений континуальная передаточная функция примет вид:

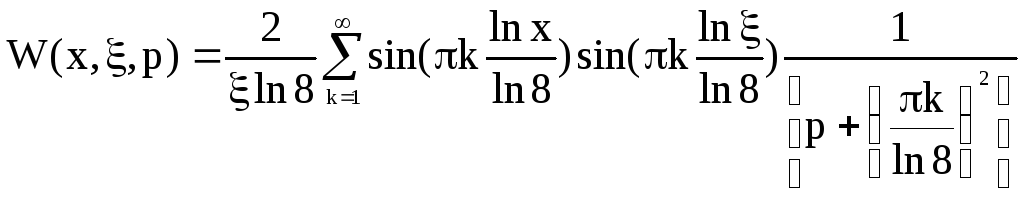
Для дальнейших расчетов найдем изображение по Лапласу для нормирующей функции:

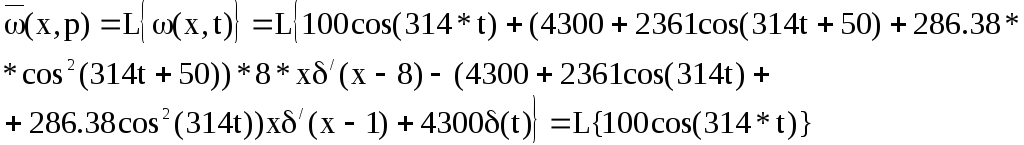Вычислим значение этого уравнение в среде MathCad и выделим компоненту входной координаты:

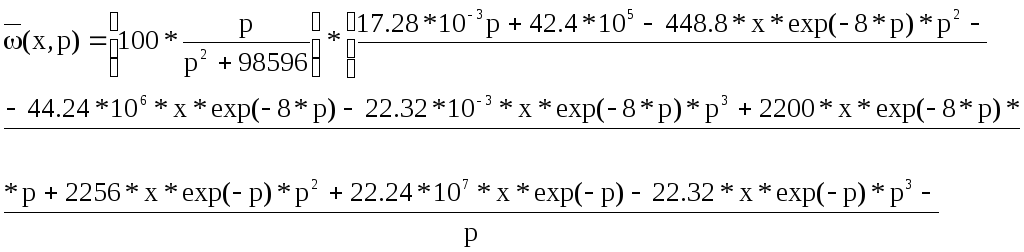
Таким образом, операторное изображение выходной величины запишется как:

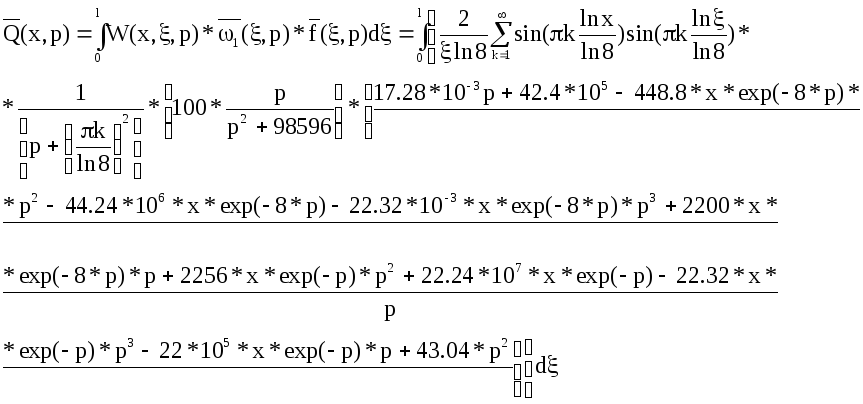Интегральная передаточная функция перепишется в виде:

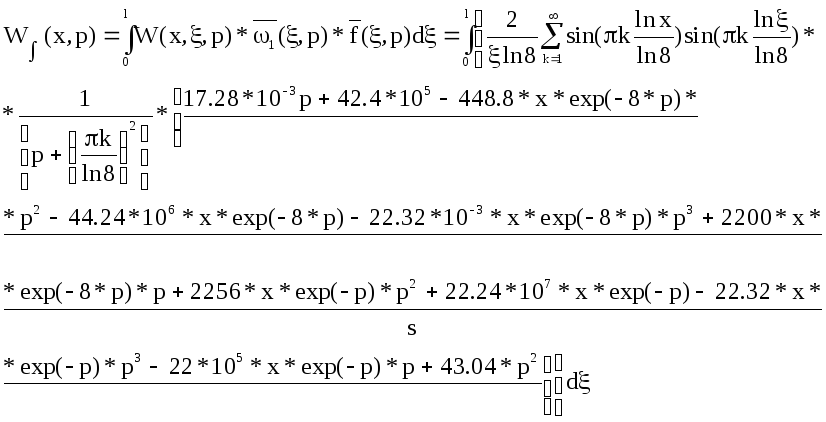
Длина нити конкретная и равна 8.

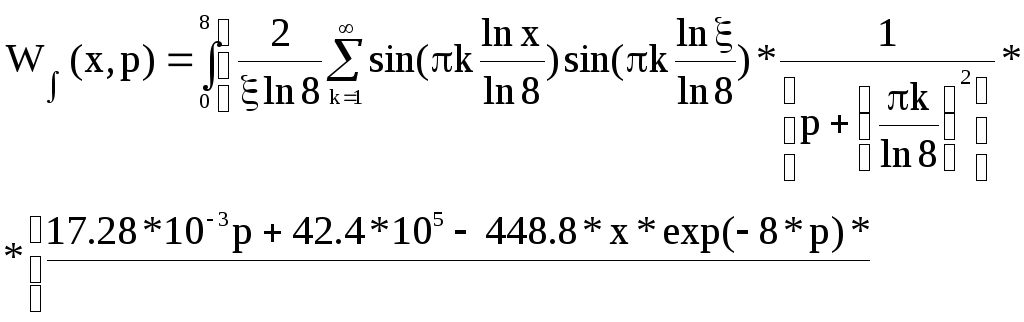
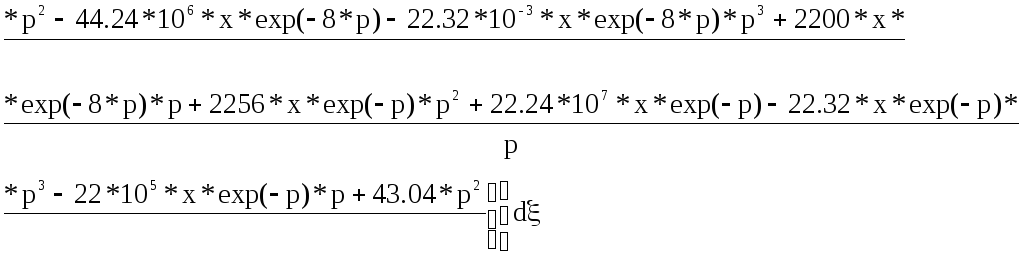
Ввиду явной неразрешимости интеграла, в котором присутствует сумма ряда до бесконечного члена, введем ограничение на количество рядов 1, т.е. возьмем первый член ряда. Эта мера является вынужденной и ведет к большой погрешности.

Таким образом, учитывая принятые меры, получим уравнение:

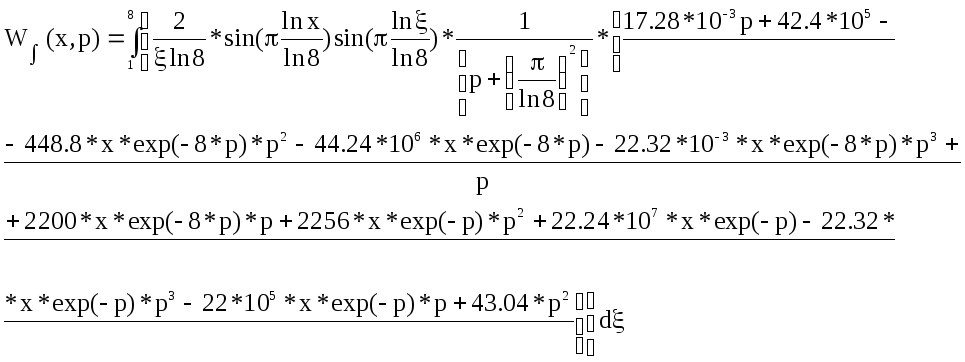
Путем применения пакета MathCad, была получена следующая форма передаточной функции:

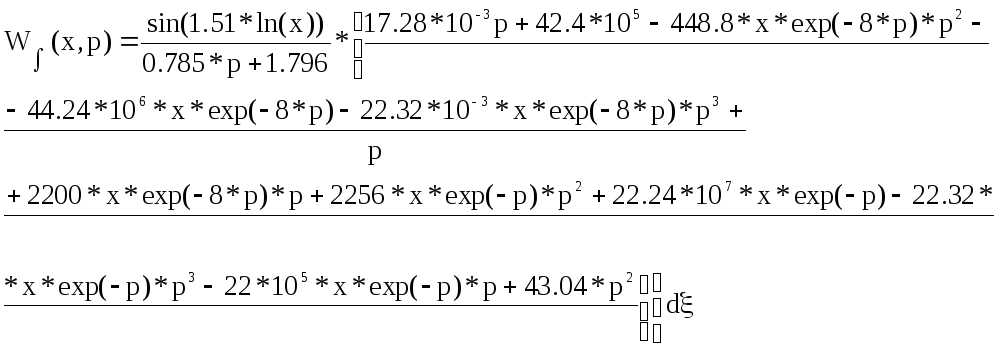
Координата x пробегает по длине стержня, однако можно предположить, что закон изменения состояния провода одинаков для всей его длины и отличается лишь коэффициентами. Будет правильным приравнять x к какому либо числу, например 8 (конечная точка).

После ряда упрощений и замены p на jω, было получено уравнение:

Действительная часть:

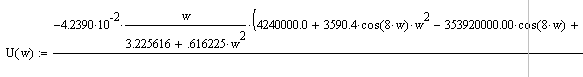
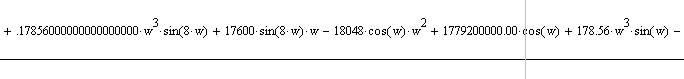
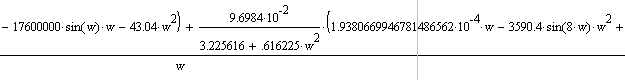
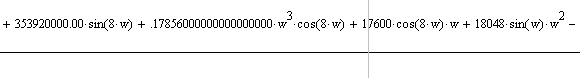
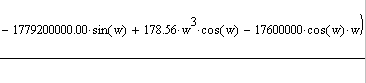
Мнимая часть:

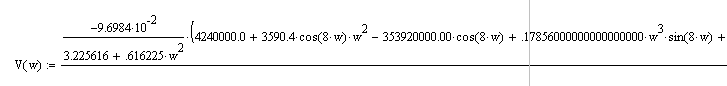
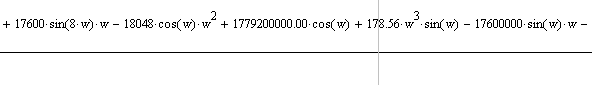
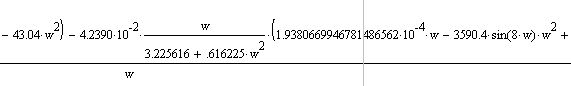
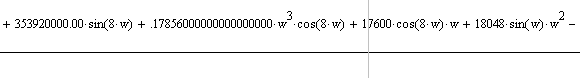
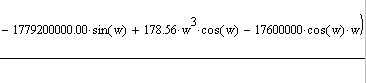
Логарифмическую амплитудно-частотную характеристику строим согласно формуле:

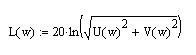
Сопрягающие частоты:

ω₁=1 Гц Т₁=1 с

ω₂=10 Гц Т₂=0.5 с

ω₃=150 Гц Т₃=0.0067 с

ω₄=200 Гц Т₄=0.005 с

ω₅=300 Гц Т₅=0.0033 с

Коэффициент: K₁=10⁸. Т.е. аппроксимированная передаточная функция запишется в виде:

На рисунке 7 представлены ЛАЧХ: фактическая (L(ω)) и аппроксимированная (N(ω)).

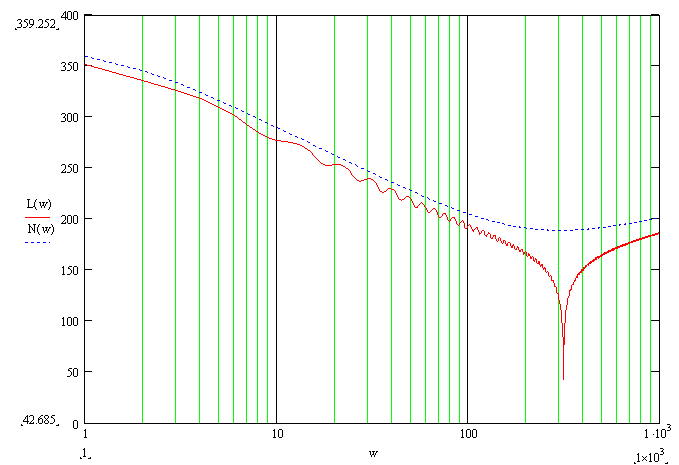
Рисунок 7

Логарифмическую фаза-частотную характеристику, строим согласно формуле:

График аппроксимированной ЛФЧХ строится по формуле:

Графики ЛФЧХ представлены на рисунке 8, где Ψ(ω)-фактическая, S(ω)-аппроксимированная ЛФЧХ.

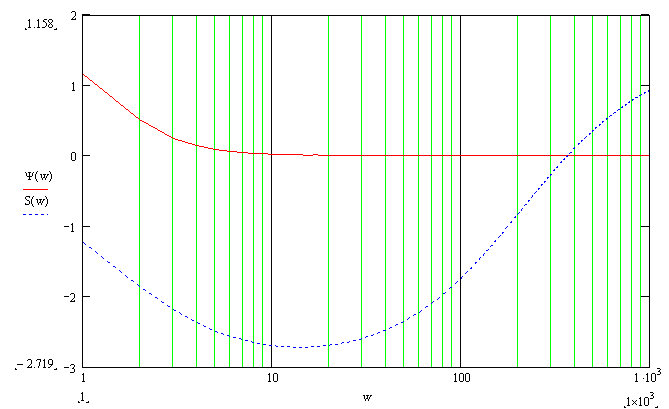
Рисунок 8

ЗАКЛЮЧЕНИЕ

В ходе курсовой работы было рассмотрено устройство металлического терморезистора, была получена передаточная функция устройства. В дальнейшем была получена передаточная функция платиновой нити (составной части терморезистора), которая отличалась от передаточной функции всего устройства. Таким образом, обнаружено действие СРП и ССП, которые в сумме дают известную передаточную функции, в отдельности далеки от нее. Кроме того, были построены ЛАЧХ и ЛФЧХ нити, которые также далеки от подобных характеристик металлического терморезистора в целом.

В целом была на практике изучена методика исследования системы с распределенными параметрами