БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ

КАФЕДРА УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ

КУРСОВАЯ РАБОТА

по дисциплине

МОДЕЛИРОВАНИЕ СИСТЕМ УПРАВЛЕНИЯ

МЕТАЛЛИЧЕСКИЙ ТЕРМОРЕЗИСТОР

Выполнил ст. гр. УИТ-41

Сербаев В.В.

Принял преподаватель

Мефёдова Ю.А.__________

«____» _____________2004г.

2004

СОДЕРЖАНИЕ

Введение 3

1 Назначение, принцип действия, конструкция 4

металлического терморезистора

2 Представление устройства в виде структурной схемы 10

3 Общие сведения об основных характеристиках СРП 11

4 Синтез интегральной передаточной функции СРП 15

Заключение 23

Список использованной литературы 24

ВВЕДЕНИЕ

Первый этап в развитии ТАУ был связан с управлением системами, состояние которых характеризуется поведением во времени t, некоторого набора конечного числа n-функций одной переменной t.

Подобные системы описываются обыкновенными дифференциальными уравнениями относительно Q(t) и называются системами с сосредоточенными параметрами (ССП).

Модели большего числа ОУ могут быть с достаточной для практических целей точностью отнесены к классу ССП.

Системы, состояние которых описывается формулами нескольких аргументов зависящих от времени, так и от пространственных координат получим название СРП.

ССП являются частным случаем СРП и используются для упрощения и решения задач на первом (нулевом) уровне. Но не все среды могут быть описаны такими уравнениями, в это главный недостаток систем с сосредоточенными параметрами.

Целью курсовой работы является синтез интегральной передаточной функции для объектов управления с распределенными параметрами. В ходе курсовой работы предлагается идентифицировать ДУ, определить континуальную передаточную функцию и нормирующую функцию, синтезировать интегральную передаточную функцию, построить ЛАЧХ и ФЧХ, аппроксимировать характеристики, получить выражение для оценочной интегральной передаточной функции.

1 Назначение, принцип действия, конструкция металлического терморезистора

Металлический терморезистор – электрический прибор, предназначенный для непосредственного измерения температурных параметров в различных средах.

Принцип действия основан на изменении сопротивления материала проводника в зависимости от его температуры (увеличение проводимости с повышением температуры).

Терморезисторы представляют собой металлическую проволоку или ленту, намотанную на жесткий каркас из изолирующего материала (кварц или др.). Конструкция представлена на рисунке 1, где: 1 – платиновая спираль, расположенная между двумя изоляционными слоями; 2 – керамика; 3 – вывод; 4 – внутренняя или внешняя крепежная трубка (платиновая); 5 – защитный кожух; 6 – защитный корпус (платиновый); 7 – вывод; 8 – керамическая трубка; 9 – платиновая проволока. Работают в комплекте с мотами измерительными, потенциометрами или логометрами.

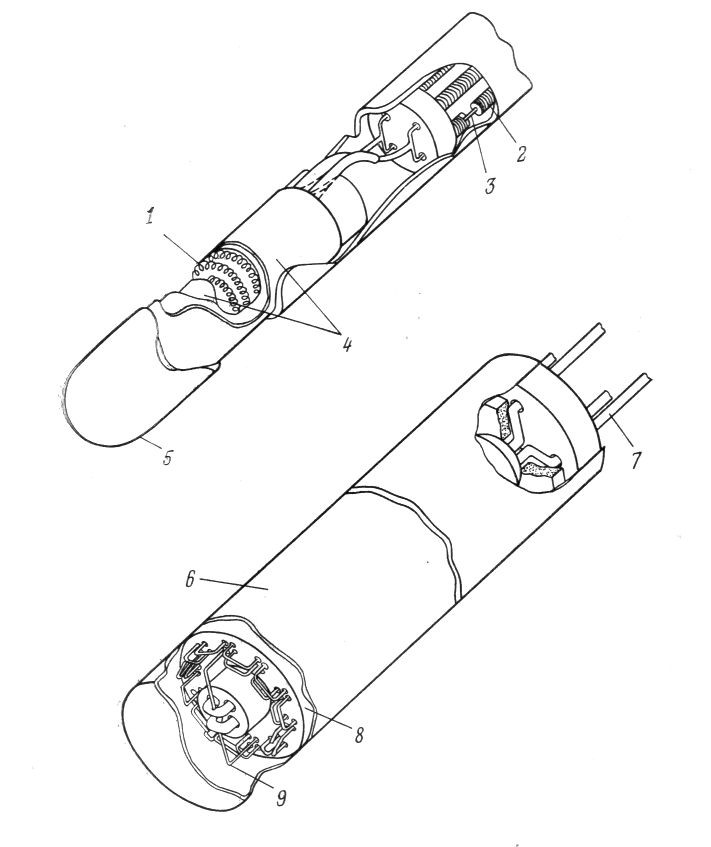
Рисунок 1 – Конструкция металлического терморезистора (платиновый)

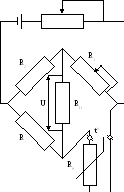
Рисунок 2 – Схема включения металлического терморезитора

Изменение сопротивления вследствие нагрева ΔR=Rα_RΔT создает измеряемое изменение напряжения v = ΔRi, где i – измеряемый ток (который ограничен величиной, составляющей несколько миллиампер, с целью снижения саморазогрева зонда). Поэтому, чтобы получить достаточно высокую чувствительность, необходимо использовать сравнительно большие сопротивления, что достигается уменьшением площади поперечного сечения проволоки (которое ограничено условием обеспечения механической прочности) и увеличением ее длины (которое ограничено допустимыми габаритами измерительной установки).

Электрический ток в металлах представляет собой движение свободных электронов. Идеальная кристаллическая решетка не создает сопротивления для их движения, и ее электрическое сопротивление равно нулю. Причиной сопротивления является неидеальная периодичность кристаллической решетки, которая обусловливается, с одной стороны, тепловыми колебаниями атомов, и, с другой стороны, нарушениями периодичности, или дефектами кристаллической решетки. Согласно классической теории, электрон (массой m с зарядом q), ускоренный электрическим полем Е, претерпевает столкновения, при которых его скорость каждый раз обращается в нуль. Обозначим через τ время релаксации - среднее значение интервала времени между двумя соударениями, через n_C=1/τ - среднее число соударений в секунду. Уравнение движения электрона в направлении приложенного электрического поля

позволяет определить среднюю скорость перемещения электронов:

Если число свободных электронов в единице объема равно N, то плотность тока будет определяться уравнением

а удельное сопротивление выражается формулой

Все физические величины, влияющие на τ и, следовательно, на число соударений в секунду, влияют на удельное сопротивление.

Влияние температуры. Каждый атом кристаллической решетки (массой М) колеблется относительно своего среднего положения, и на него действует восстанавливающая сила Сх (х - отклонение от положения равновесия). Уравнение движения

позволяет определить среднюю потенциальную энергию атома w =¹/2Cx² и частоту колебаний.

Характеристическая дебаевская температура θ определяется соотношением

где h=6,626*10^-34 Дж*С - постоянная Планка, k=l,38*10^-23 Дж*К^-1 - постоянная Больцмана. Эта температура равна 375 К для Ni, 333 К для Сu и 240 К для Pt. При T>θ

Время релаксации τ обратно пропорционально х², поэтому при T>θ

Но на самом деле в рассматриваемой области температур удельное сопротивление изменяется не строго линейно, что объясняется, в зависимости от конкретных условий, расширением кристаллической решетки с ростом температур и влиянием на т энергии электронов. При низких температурах (Т<<θ) удельное сопротивление не является квазилинейной функцией Т и уменьшается быстрее с падением температуры - обычно как Тⁿ (n>1).

Влияние примесей и дефектов кристаллической решетки. Наличие примесей или дефектов кристаллической решетки увеличивает частоту соударений; к числу соударений, обусловленных тепловыми колебаниями, n_с(Т), прибавляется число столкновений, обусловленных примесями внедрения и дефектами кристаллической решетки n_c(i):

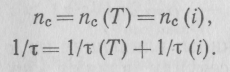
Предыдущее выражение для удельного сопротивления распадается соответственно на два члена:

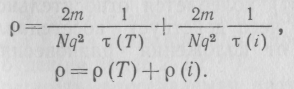
При очень низких температурах ρ(T)<<ρ(i), т. е. удельное сопротивление перестает зависеть от температуры и зависит только от концентрации примесей и дефектов кристаллической решетки металла. В этом состоит правило Маттисена.

Чувствительность к температуре а_р определяется соотношением

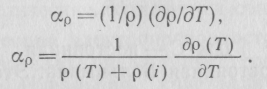
Наличие атомов внедрения или структурных дефектов, учитываемое членом p(i) приводит к снижению чувствительности. Этим объясняется важность чистоты металлов и отсутствия внутренних напряжений для обеспечения максимальной, и строго определенной чувствительности к температуре.

Зависимость сопротивления от температуры.

Платина. В диапазоне температур приблизительно от -200 до 650°С по величине сопротивления проволоки из очень чистой платины можно определить температуру (с погрешностью, не превышающей -0,1°С) по формуле Календара - ван Дюсена:

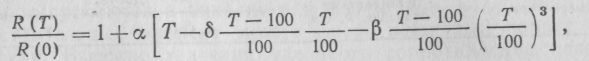
где Т выражается в °С и β=0 при T>0°С. Экстраполяция этой формулы до температуры затвердевания золота, равной 1064.43 °С при нормальном атмосферном давлении, приводит к погрешностям, не превышающим 2°С. Формула Календари - ван Дюсена эквивалентна соотношению

где A=α(1+δ/100), В=-αδ*10⁴, С=-αβ*10^-8 при T<0°С и С=0 при T>0°С. Четыре значения сопротивления К, измеренные при точно известных температурах, позволяют определить требуемые характеристики. Здесь R(0) - сопротивление, измеренное при температуре 0°С; α вычисляется по предыдущей величине и сопротивлению, измеренному при температуре 100°C: а=[R(100)-R(0)]/100R(0); δ можно вычислить, измерив сопротивление, например, при температуре кипения серы (444,4 °С при нормальном атмосферном давлении).

Величина β определяется путем измерений при низкой температуре, обычно при температуре кипения кислорода (-182,97°С при нормальном атмосферном давлении).

Для резисторов из платины высокой чистоты, не имеющей внутренних механических напряжений, изготовитель датчиков (фирма Rosemount) приводит следующие значения: α=0,00392, β=1,492, δ=0,11 при T<0°С и β=0 при Т>0°С. Отсюда A=3,90802*10^-3; В=5,80195*10^-7; С=-4,27350*10^-12 при T<0°С и С = 0 при T>0°С.

Сопротивление из никеля. В диапазоне температур от -60 до +70°С зависимость сопротивления никеля от температуры удовлетворительно описывается формулой

где Т выражается в °С, R₀ - сопротивление при температуре 0°С, А=5,49167*10^{-3 0}С и В=6,666667*10^{-6 0}C^-1.

В стандарте DIN 43760 приведен ряд значений сопротивления в диапазоне температур от -60 до 180 ⁰С, а также величины допусков.

Зависимость электрического сопротивления проводника от его температуры выражается формулой: , где θ – температура проводника; R₀ – сопротивление проводника при температуре θ₀; φ(θ-θ₀) - определенная функция разности температур. В широком диапазоне температур функция φ(θ-θ₀) хорошо аппроксимируется экспоненциальной зависимостью φ(θ-θ₀)=e^-α(θ-θ0).

В узком диапазоне температур функция φ(θ-θ₀) с достаточной точностью аппроксимируется полиномом φ(θ-θ₀)=1+α(θ-θ₀)+β(θ-θ₀)²+…

Коэффициенты α, β, … в выражениях определяются экспериментально.

Получим зависимость температуры проводника θ от температуры среды τ, в которой он находится. Для этого вычислим изменение количества тепла dQ, содержащегося в проводнике, при изменении его температуры на dθ: dQ=mc*dθ, где с – теплоемкость материала проводника, m – его масса. С другой стороны, согласно закону Ньютона, количество тепла, получаемое датчиком от внешней среды, пропорционально разности температур среды и датчика, площади поверхности датчика и времени:dQ=kS(τ-θ)dt, где k – коэффициент теплоотдачи. На основании закона сохранения энергии левые части в уравнениях равны. Поэтому вытекает дифференциальное уравнение, связывающее температуру датчика θ и температуру среды τ: T θ+θ=τ, где T=cm/kS – постоянная времени термосопротивления. На основании полученных уравнений термосопротивление можно представить в виде последовательного звена и нелинейности с экспоненциальной или квадратичной характеристикой.

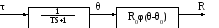
Рисунок 4

Используя приведенные выше уравнения и табличные данные получим:

T=cm/kS=0.13*0.02/20*0.005=0.026

За начальное сопротивление проводника примем (температура 20⁰С)

4.3 кОм.

Таким образом передаточная функция запишется в виде: