САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

КАФЕДРА УИТ

КУРСОВАЯ РАБОТА

по курсу: «Моделирование систем управления»

Тема: «Расчет системы с распределенными параметрами»

Выполнил: ст. гр. УИТ-42

Фральцов А.Б.

Принял: преп. кафедры

Фролова М. А.

Балаково 1999.

Д.у.:

Н.у.:

Г.у.:

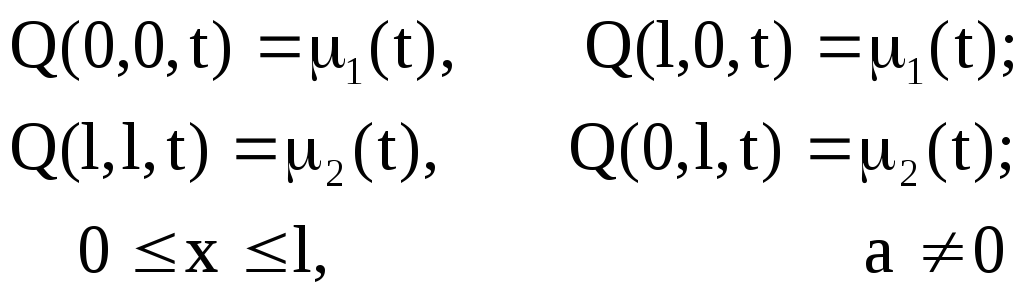
Задание: .

По заданному дифференциальному уравнению получить выражение для передаточной функции в распределенных параметрах, выражение для выходной величины, выражение для оценочной передаточной функции для наилучших условий управления. Построить оценочную ЛАЧХ, аппроксимировать ее с погрешностью 5% инерционно-форсированными звеньями и записать выражение передаточной функции через типовые звенья.

Решение.

По виду уравнения (1) определяем, что это двумерное волновое уравнение описывает продольные колебания мембраны постоянной плотности. По виду граничных условий определяем, что края мембраны движутся по некоторому заданному закону: η₁ и η₂ .

Пусть начальные условия нулевые:

Зададим граничные условия. Пусть один край мембраны жестко закреплен, а второй движется по заданному закону:

Зададим входное воздействие:

Тогда нормирующая функция (2) примет вид:

Найдем вариации отклонения:

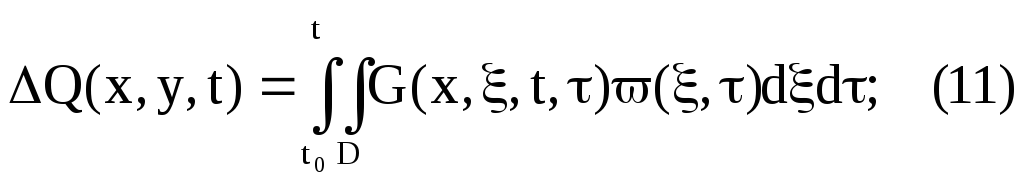
Используя выражение (3), получим:

Преобразуем (5) по Лапласу:

где континуальная передаточная функция;

изображение по Лапласу.

Найдем изображение по Лапласу нормирующей функции:

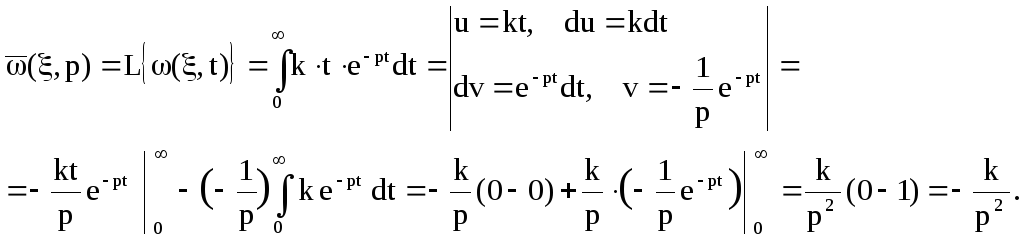
Найдем континуальную передаточную функцию

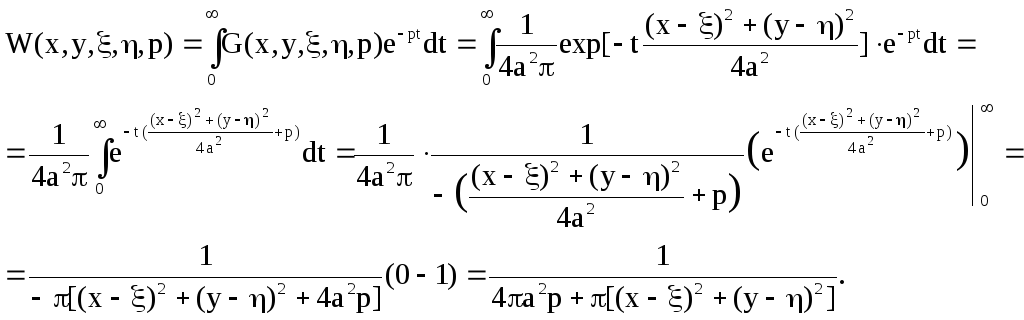
Подставляем найденную континуальную передаточную функцию и изображение по Лапласу от нормирующей функции в (6), получим функцию изображение по Лапласу от входной функции:

;

Т.к. , то

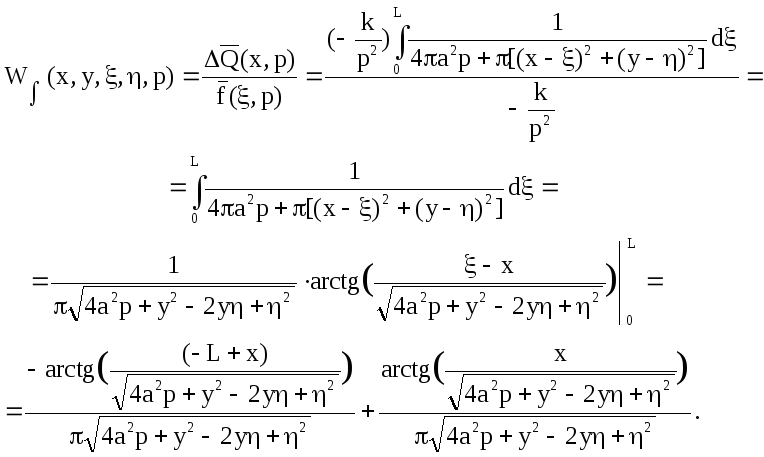
Для построения ЛАЧХ в полученной интегральной передаточной функции заменим р на jω и затем воспользуемся формулой:

Выполним расчет и построение ЛАЧХ с помощью программы Matchcad 2000, задав произвольно необходимые параметры (см. рис.1).

Аппроксимируем полученную ЛАЧХ с погрешностью 5%.

20lg k = 30,676 , откуда k = 10 ^{(30,676 / 20)} = 0,0292

ω = 1 , T = 1/ω = 1.

В результате аппроксимации получили произведение интегрирующего и инерционного звена первого порядка.

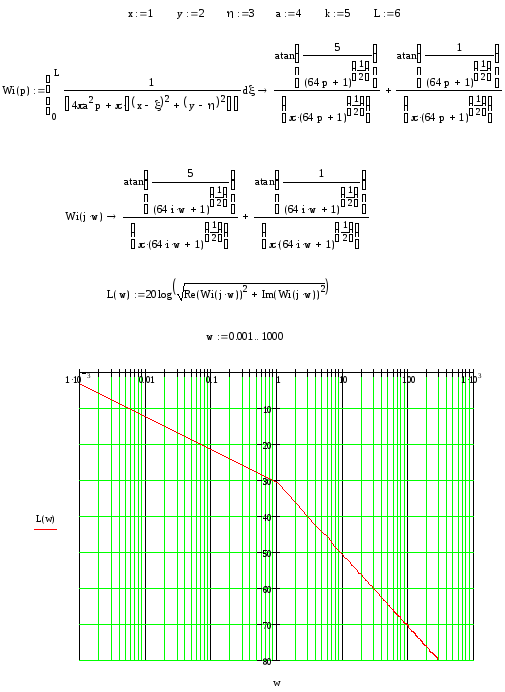Рис.1. Оценочная логарифмическая амплитудо-частотная характеристика