Балаковский Институт Техники Технологии и Управления

Факультет: вечерне-заочный

Специальность: УИТ

МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКОЙ СИСТЕМЫ МЕТОДОМ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА

Вариант 8

Выполнил: ст. гр. УИТ-51в

Проверил:

Балаково-2004

СОДЕРЖАНИЕ

Задание на работу.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . …....	2
ВВЕДЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . …....	3
ОСНОВНАЯ ЧАСТЬ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ……	4
Построение плана матрицы . . . . . . . . . . . . . . . . . . . . . . . . . . .…...	4
Расчет линейной модели . . . . . . . . . . . . . . . . . . . . . . . . . . . ….. …..	6
Оценка адекватности модели .. .. . . . . . . . . . . . . . . . . . . . . . . …….	7
Расчет крутого восхождения . .. . . . . . . . . . . . . . . . . . . . . . . . …….	8
ЗАКЛЮЧЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . …...	10

Задание

1. Построить матрицу планирования.

2. Построить линейную модель.

3. Оценить адекватность модели.

4. Оценить коэффициенты модели.

5. Провести крутое восхождение.

Исходные данные

План 23

Таблица 1

Уровни факторов	Факторы процесса
	X1	X2	X3
Нижний	6	40	0.22
Основной	10	80	0.40
Верхний	14	120	0.58

Массив данных

Таблица 2

Y1	Y2	Y3	Y4
0.12	1.12	0.1	0.12
0.06	0.07	0.07	0.08
0.20	0.18	0.21	0.20
0.18	0.16	0.15	0.17
0.13	0.12	0.14	0.16
0.11	0.12	0.10	0.10
0.24	0.23	0.22	0.21
0.20	0.21	0.20	0.18

Введение

В процессе развития общества человеком устанавливаются закономерности процессов в различных явлениях и областях: физике, химии, биологии и многих других. Первичными в процессе познания являются результаты наблюдений, представляющие собой отправной пункт к построению модели явления или процесса.

Построение моделей по результатам наблюдений представляет собой формализацию, необходимую для определения основных признаков, связей и закономерностей, присущих объекту, и отсеивания второстепенных признаков. В качестве динамических объектов могут рассматриваться технические системы и процессы в них. Для одного и того же объекта в зависимости от конкретных требований практики и типа решаемой задачи может быть построен ряд моделей различной сложности.

В данной курсовой работе решается вопрос построения моделей на основе экспериментальных данных.

Цель работы – изучение метода планирования эксперимента при исследовании многофакторной динамической системы и его применения для получения линейной математической модели и проверки ее адекватности.

Составление матрицы планирования.

Проведем оптимизацию полного факторного эксперимента. Для полного факторного эксперимента, в котором реализуются все возможные сочетания уровней факторов, число опытов определяется по следующей формуле: N = 2^k. Будем рассматривать задачу с максимальным числом факторов равным трем и числом опытов 2³=8.

1. Составим матрицу планирования.

На основании заданных данных построим матрицу планирования.

Первоначально введем условное обозначение верхнего(+) и нижнего(-) уровня.

Таблица №3

№		х1		х2		х3						S
1	-		-		-		0,113		0,016		0.546		0,109		0,0000188
2	+		-		-		0,07		0.017		0.131		0,075		0,0000250
3	-		+		-		0,198		0.0004		0.021		0,199		0,0000022
4	+		+		-		0,165		0.001		0.025		0,165		0,0000000
5	-		-		+		0,138		0.003		0.055		0,139		0,0000022
6	+		-		+		0,108		0.008		0.088		0,105		0,0000062
7	-		+		+		0,225		0.003		0.050		0,229		0,0000160
8	+		+		+		0,198		0.0004		0.021		0,195		0,0000063

1. Подсчитываем средние значения в сериях каждого опыта.

(1)

где у_i – i-ое значение в серии опытов; n – количество опытов в серии.

2. Подсчитываем дисперсию S² различных серий опытов.

(2)

3. Квадратичная ошибка или стандарт:

. (3)

Проверяем вторую серию опытов (с максимальным значением дисперсии S²=0.017) на наличие ошибки с помощью критерия Стьюдента: ,

где t – табличное значение критерия Стьюдента.

Коэффициент Стьюдента для степени свободы (n – 1)=(4 – 1)=3 равен t=3,18.

Значение 1-ого опыта, равное 1.12 – промах, из рассмотрения исключаем.

Проверяем дисперсию на однородность.

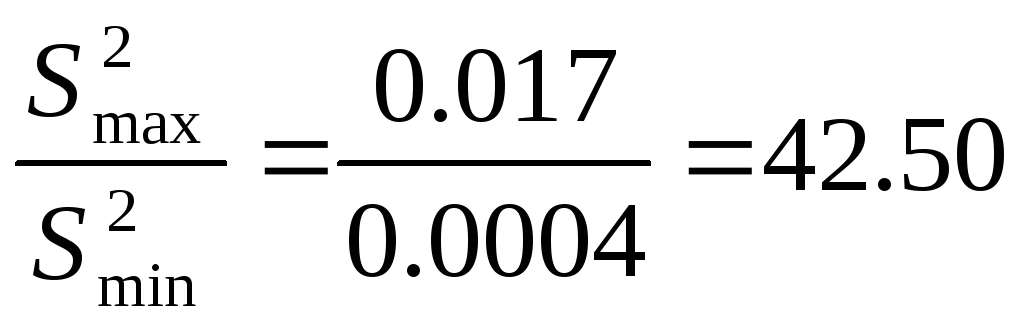(4)

Полученное значение больше табличного значения критерия Фишера равного F=9.3 для степеней свободы числителя f₁=n–1=4-1=3 и знаменателя f₂=n–1=4-1=3, значит дисперсия неоднородная.

Находим дисперсию выходного параметра.

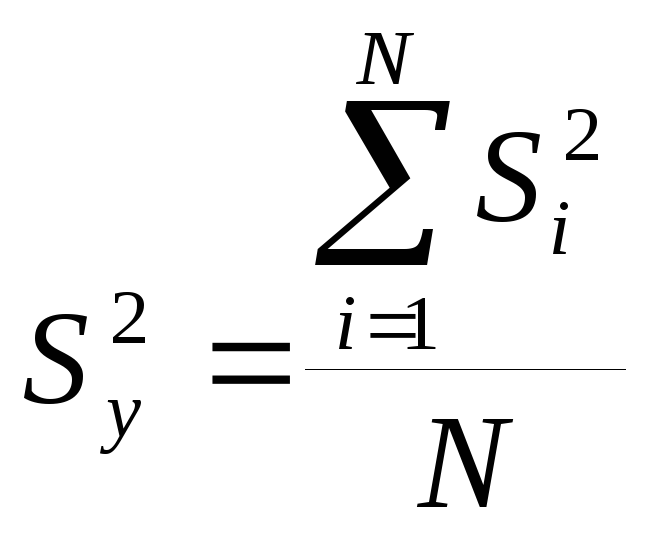, (5)

РАСЧЕТ ЛИНЕЙНОЙ МОДЕЛИ

у=b₀+b₁х₁+b₂х₂+ b₃х₃ (6)

Рассчитаем коэффициенты для линейной модели (b₀,b_1,b_2,b₃)

по формуле: b_i= (7)

Получим следующие коэффициенты:

b₀=

b₁=

b₂=

b₃=

Тогда линейная модель запишется в виде:

у=0,152-0,017х₁ +0,045х₂+0,015х₃ (9)

Определяем по этой модели расчетные значения параметра оптимизации

= f(x) и заносим эти значения в таблицу.

После чего находим квадрат отклонения экспериментального значения от расчетного: (10)

Заносим полученные значения в таблицу.

После построения модели необходимо провести проверку ее адекватности.

ОЦЕНКА АДЕКВАТНОСТИ МОДЕЛИ.

Найдём дисперсию адекватности по следующей формуле:

(11)

где f = N – (n + 1) =8-(3+1)=4

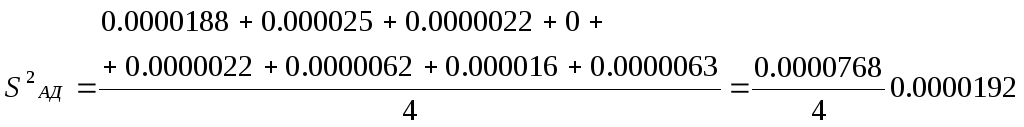
Проверяем модель на адекватность, для чего находим расчетный коэффициент Фишера:

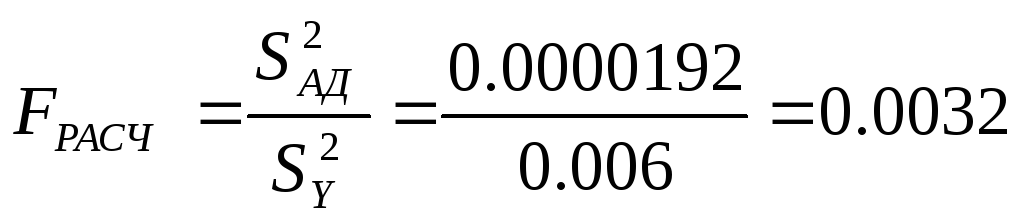(12)

Полученное значение сравниваем с табличным значением критерия Фишера F=9,1 для f₁=4 и f₂=3 и поскольку полученное значение не превышает его, то полученная линейная модель адекватна.