курсовая работа / МСУ3

Основная часть

Для исходных данных составим матрицу планирования. Число опытов определяется по формуле:

N=2^k,

где N – число опытов,

k – число факторов.

В нашем случае:

N=2³=8.

Так как в эксперименте реализуются все возможные сочетания факторов, он будет называться полным факторным экспериментом.

Введем обозначение: верхний уровень факторов процесса (+), основной уровень (0) и нижний уровень (-).

Составим матрицу планирования (таблица №1).

Таблица №1

№	Факторы			Значения параметра оптимизации					S2 *10-4	f
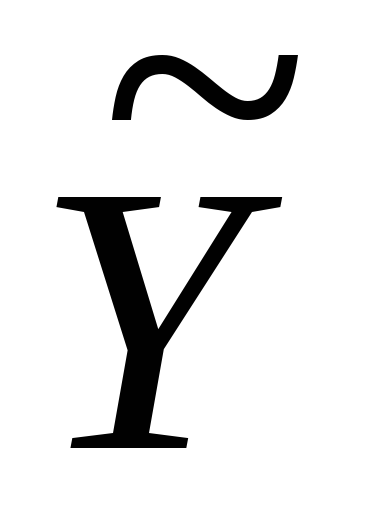
	X1	X2	X3	Y1	Y2	Y3	Y4
1	-	-	-	0.12	1.1	0.11	0.12	0.117	0.335	1	0.11
2	+	-	-	0.06	0.06	0.06	0.08	0.065	1	2	0.074
3	-	+	-	0.2	0.18	0.22	0.2	0.2	2.7	2	0.202
4	+	+	-	0.18	0.16	0.18	0.16	0.17	1.3	2	0.166
5	-	-	+	0.14	0.12	0.14	0.16	0.14	2.7	2	0,142
6	+	-	+	0.11	0.12	0.1	0.1	0.1075	0.96	2	0.106
7	-	+	+	0.24	0.23	0.24	0.21	0.23	2	2	0.234
8	+	+	+	0.2	0.22	0.2	0.18	0.2	2.7	2	0.198

Каждый эксперимент содержит элемент неопределенности вследствие ограниченности экспериментального материала. Постановка параллельных опытов не дает полностью совпадающих результатов, так как всегда существует ошибка опыта. В первой строке матрицы планирования значение параметра оптимизации Y₂=1,1 существенно отличается от других значений. Проверим значение параметра Y₂ на возможность ошибки. Ошибка опыта может быть определена следующим образом:

1. найдем среднее арифметическое результатов:

,

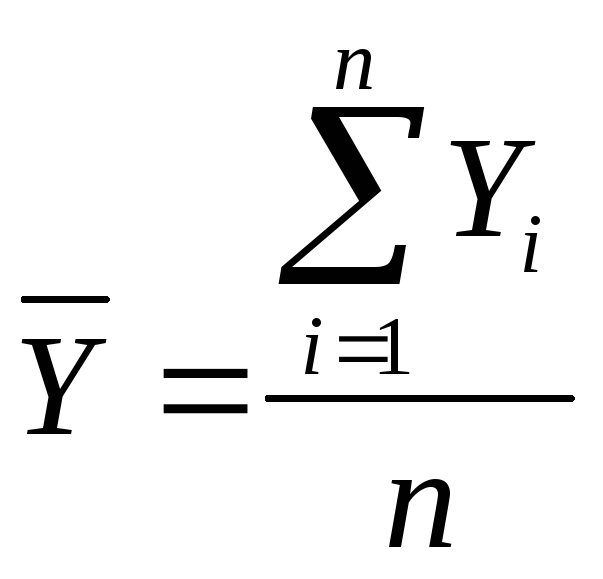
где n – число опытов в серии,

;

2. найдем дисперсию:

,

где (n-1) – число степеней свободы,

;

3. найдем квадратичную ошибку:

,

,

для определения ошибок опыта используем критерий Стьюдента:

,

где t – табличное значения критерия Стьюдента.

,

, значит Y₂=1,1 является ошибкой.

Для каждой серии опытов найдем среднее арифметическое значение и дисперсию:

Полученные дисперсии проверим на однородность. Однородность дисперсий означает, что среди всех суммируемых дисперсий нет таких, которые бы значительно превышали все остальные. Проверку однородности дисперсий проведем по критерию Фишера. Для этого найдем отношение:

Полученное значение сравним с табличным. Если критерий Фишера, полученный расчетным путем, меньше табличного, то дисперсии однородны.

,

сравним полученное значение с табличным: 80,6<19,2, следовательно, дисперсии однородны.

Найдем дисперсию параметра оптимизации:

,

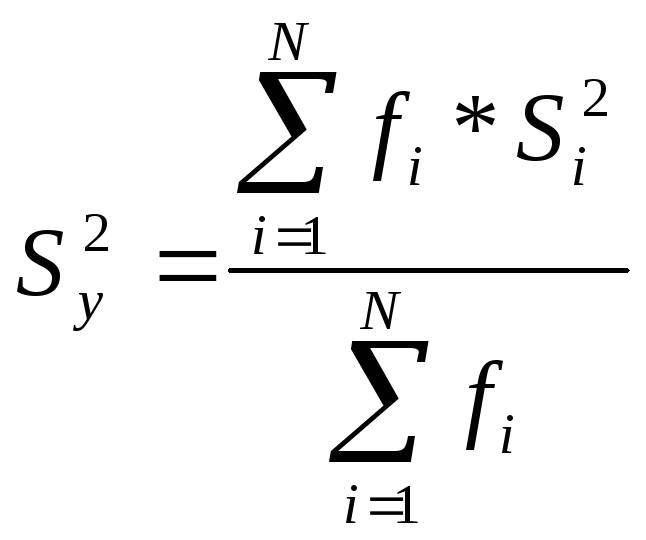
где f_i – число степеней свободы в i-том опыте.

Построим линейную модель:

Коэффициенты линейной модели определяются по формулам:

,

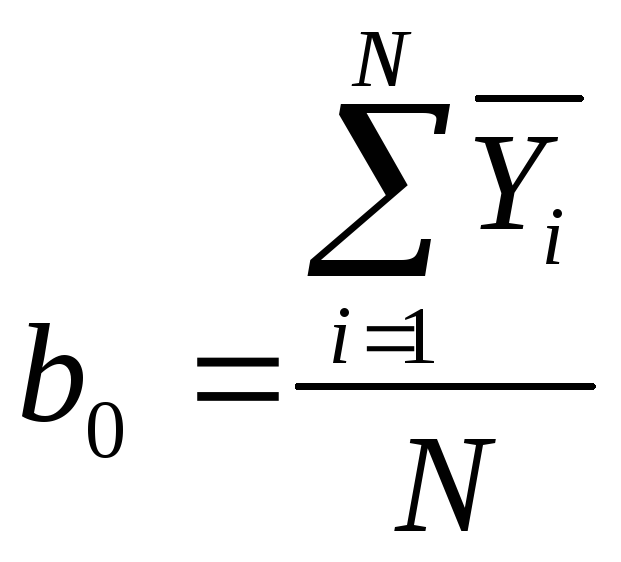Коэффициент b₁ определяется как среднее арифметическое , взятых со знаками первого столбца таблицы №1:

Коэффициент b₂ определяется как среднее арифметическое , взятых со знаками второго столбца таблицы №1:

Коэффициент b₃ определяется как среднее арифметическое , взятых со знаками третьего столбца таблицы №1:

Запишем линейную модель:

По полученной линейной модели рассчитаем значение параметра оптимизации для каждой серии опытов:

Полученную модель проверим на адекватность. Для этого вычислим дисперсию адекватности по формуле:

,

где ,

N – число серий опытов,

k – количество факторов.

+

+

Для проверки адекватности модели используется Ф-критерий Фишера, который определяется формулой:

,

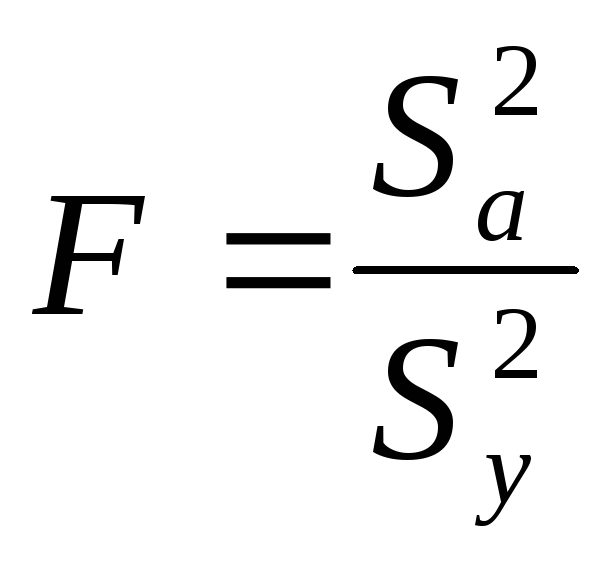если табличное значение критерия больше расчетного, модель адекватна.

Сравним с табличным значением: 0,24<3,3, следовательно, модель адекватна.

Проведем проверку значимости каждого коэффициента. Для этого рассчитаем дисперсию коэффициента регрессии по формуле:

Дисперсии всех коэффициентов равны друг другу, так как они зависят только от ошибки опыта и числа опытов.

На основе полученной дисперсии коэффициентов регрессии построим доверительный интервал по формуле:

,

где - квадратичная ошибка коэффициента регрессии,

t – табличное значение критерия Стьюдента.

Коэффициент является значимым, если его абсолютная величина больше доверительного интервала. Проведем оценку коэффициентов:

=0.154>0.01

=0.018>0.01

=0.046>0.01

=0.016>0.01

В нашей линейной модели все коэффициенты являются значимыми.

Проведем движение по градиенту, на основе которого исследуем поведение объекта в точках, отличных от заданных. Движение к точке стационарной области называется крутым восхождением.

Для определения шага движения найдем величины, пропорциональные составляющим градиента:

J_j*b_j

Для каждого фактора увеличим это число в 2 раза и проведем расчет мысленных опытов.

Результаты запишем в таблицу №2:

Таблица №2

Результаты мысленных опытов

Факторы	Х1	Х2	Х3
-1	6	40	0.22
0	10	80	0.4
+1	14	120	0.58
Jj	4	40	0.18
bj	-0.018	0.046	0.016
Jj*bj	-0.072	1.84	0.0029
шаг	0.144	3.68	0.0058
1	9.856	83.68	0.4058
2	9.712	87.36	0.4116
3	9.568	91.04	0.4174
4	9.424	94.72	0.4232
5	9.28	98.4	0.429
6	9.136	102.08	0.4348
7	8.992	105.76	0.4406
8	8.848	109.44	0.4464
9	8.704	113.12	0.4522
10	8.56	116.8	0.458

Перейдем к кодированным значениям по формуле:

,

где X_j – натуральное значение фактора,

X_j0 – натуральное значение основного уровня,

- кодированное значение фактора,

J_j – интервал варьирования.

Рассчитаем значения параметра оптимизации и запишем их в таблицу №3:

Таблица №3

№ опыта	X1	X2	X3
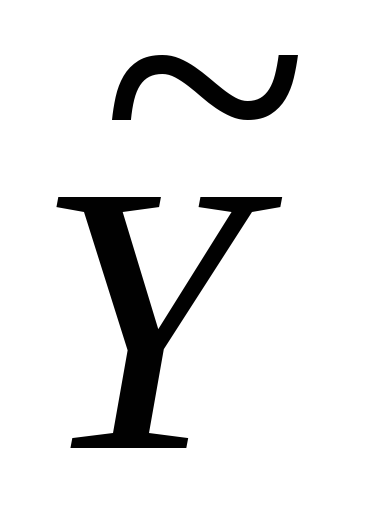
1	-0,036	0,092	0,0322	0,1594
2	-0,072	0,184	0,0644	0,1648
3	-0,108	0,276	0,0967	0,1702
4	-0,144	0,368	0,1289	0,1756
5	-0,18	0,46	0,161	0,181
6	-0,216	0,552	0,193	0,1864
7	-0,252	0,644	0,225	0,1917
8	-0,288	0,736	0,2578	0,1972
9	-0,324	0,828	0,29	0,2025
10	-0,36	0,92	0,322	0,2079

Вывод

Реализация мысленных опытов на стадии крутого восхождения не привела к улучшению значения параметра оптимизации по сравнению с лучшим результатом в матрице планирования. Наибольшее значение параметра оптимизации Y=0,23 при значениях факторов эксперимента Х₁=6, Х₂=120, Х₃=0,58.

Список используемой литературы:

1. Дейч А.М. Методы идентификации динамических объектов. – М.: Энергия, 1979. –240 с.

2. Спиридонов А.А. Планирование эксперимента при исследовании технологических процессов.- М.: Машиностроение, 1981.- 184 с.

3. РДМУ 109-77. Методические указания: Методика выбора и оптимизации контролируемых параметров технологических процессов.- М.: Изд-во стандартов, 1978.- 64 с.

4. Адлер Ю.П., Александрова И.Ф., Грановский Ю.В. и др. Об одном методе формализации априорной информации при планировании эксперимента. – М.: Наука, 1966. – 70 с.