курсовая работа / Оптимизация факторного процесса Задание №1. Вариант 13
.DOC
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
КАФЕДРА УИТ
КУРСОВАЯ РАБОТА
по курсу: «Моделирование систем управления»
Тема: «Оптимизация факторного процесса»
Выполнил: ст. гр. УИТ-41
Принял: Фролова М. А.
Балаково 1999.
Задание №1. Вариант 13.
Оптимизация центробежного преобразователя расхода
Таблица №1
|
Факторы |
Уровни факторов |
|
|
|
-1 |
+1 |
|
Х1 |
146 |
157 |
|
Х2 |
2500 |
5000 |
|
Х3 |
0.94 |
1.48 |
|
|
||
Составить 23.
Проведем оптимизацию полно факторного эксперимента.
Будем рассматривать задачу с максимальным числом факторов и числом опытов 23 =8.
Составим матрицу планирования для линейной модели в первом приближении.
Таблица №2
|
|
X0 |
X1 |
Х2 |
X3 |
|
Y |
|
S2 |
ŷ |
у2 |
||||||||||
|
1 |
+ |
- |
- |
- |
12.4 12.8 |
12.6 |
0.08 |
14.125 |
2.326 |
|||||||||||
|
2 |
+ |
- |
+ |
- |
|
16.3 ;16.7; 24 |
16.5 |
0.08 |
14.958 |
2.738 |
||||||||||
|
3 |
+ |
+ |
- |
- |
10.58 10.88 |
10.73 |
0.045 |
13.208 |
6.14 |
|||||||||||
|
4 |
+ |
+ |
+ |
- |
16.1 16.9 |
16.5 |
0.32 |
14.04 |
6.052 |
|||||||||||
|
5 |
+ |
- |
- |
+ |
21.48 21.78 |
21.63 |
0.045 |
17.173 |
19.865 |
|||||||||||
|
6 |
+ |
- |
+ |
+ |
13.16 13.9 |
13.53 |
0.274 |
18.005 |
20.026 |
|||||||||||
|
7 |
+ |
+ |
- |
+ |
15.7 15.9 |
15.8 |
0.02 |
16.255 |
0.207 |
|||||||||||
|
8 |
+ |
+ |
+ |
+ |
17.32 17.8 |
17.56 |
0.115 |
17.088 |
0.305 |
|||||||||||
№
Подсчитываем средние значения в сериях Y.
где уi – i-ое значение в серии опытов, N – количество опытов в серии.
Подсчитываем дисперсию S2 различных серий опытов.
Проверяем вторую серию опытов на наличие ошибки.
Так как дисперсия S2=0.08, то
=
26.51650429
>
t
=
12.71
где t – коэффициент Стьюдента для степени свободы (n – 1)=(2 – 1)=1.
Поэтому значение опыта – промах и из дальнейшего рассмотрения исключается.
Проверяем дисперсию на однородность.
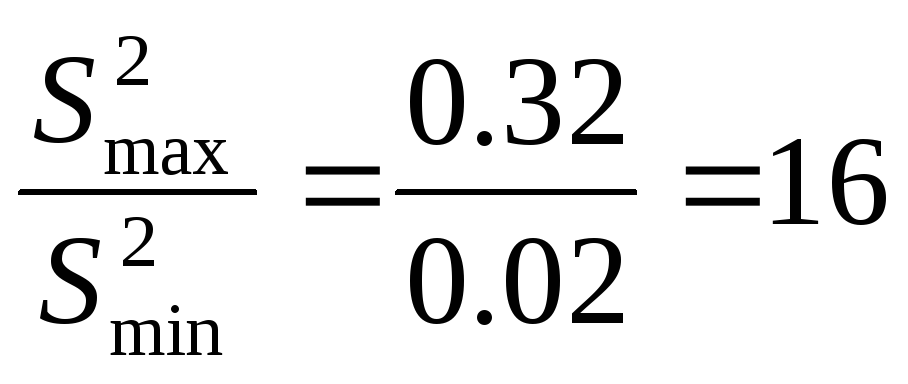
Полученное значение меньше табличного значения критерия Фишера равного F=164,4 для степеней свободы числителя f2 = n - 1=1 и знаменателя
f1 = n – 1=1, значит дисперсия однородна.
Находим дисперсию выходного параметра.
=
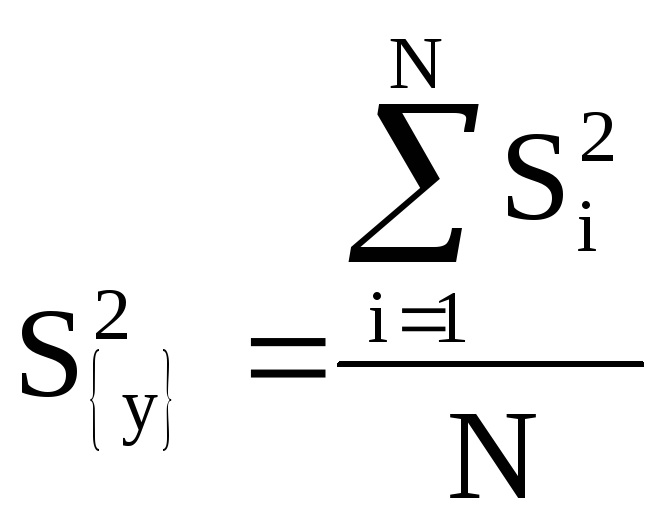0.122
Строим линейную модель
у=b0 + b1х1 + b2х2 + b3х3
пренебрегая влиянием составляющих второго порядка.
bi=
Получили следующие коэффициенты:
b0 = 15.606;
b1 = -0.459;
b2 = 0.416;
b3 = 1.524;
Линейная модель запишется в виде:
у = 15.606x0-0.459x1+0.416x2+1.524x3
Рассчитаем по этой модели расчетные значения параметра оптимизации ŷ = f(x) и занесем эти значения в таблицу.
П
осле
чего найдем квадрат отклонения расчетного
значения от экспериментального
у2 = ( ŷ - )2
и занесем полученные значения в таблицу.
Затем найдем дисперсию адекватности для равномерного дублирования
S2ад
=
=
28.61.
где f = N - (k + 1) = 8 – (4+1) = 3, n = 2.
Проверяем модель на адекватность, для чего находим расчетный коэффициент Фишера как отношение:
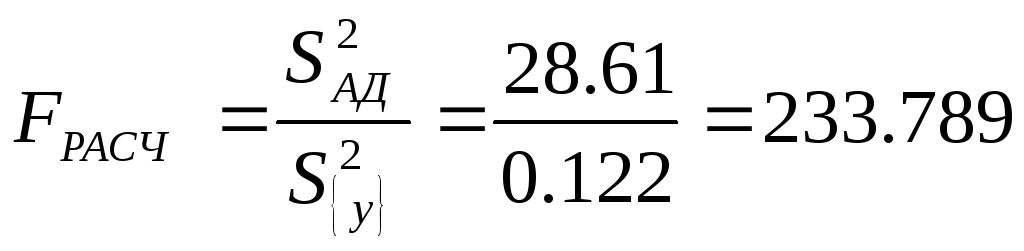
Полученное значение сравним с табличным значением критерия Фишера F = 10.1 и поскольку полученное значение больше его, то полученная линейная модель неадекватна.
Оценим значимость коэффициентов, для чего найдем дисперсию коэффициентов регрессии:
=
= 0.015.
Определим доверительный интервал
Δbj = ± t S{b} = 12,71 · 0.015 = 0,194.
Так как все коэффициенты по абсолютной величине больше доверительного интервала, то все они значимы.
Движение по градиенту.
Таблица №3
|
Натур. Значения |
Х1 |
Х2 |
Х3 |
|
У |
|
Основной ур. |
151.5 |
3750 |
1.23 |
|
|
|
Верхний ур. |
157 |
5000 |
1.48 |
|
|
|
Нижний ур. |
146 |
2500 |
0.98 |
|
|
|
J |
5.5 |
1250 |
0.25 |
|
|
|
Кодир. значения |
|
|
|
|
|
|
1 |
- |
- |
- |
12.6 |
|
|
2 |
- |
+ |
- |
16.5 |
|
|
3 |
+ |
- |
- |
10.73 |
|
|
4 |
+ |
+ |
- |
16.5 |
|
|
5 |
- |
- |
+ |
21.63 |
|
|
6 |
- |
+ |
+ |
13.53 |
|
|
7 |
+ |
- |
+ |
15.8 |
|
|
8 |
+ |
+ |
+ |
17.56 |
|
|
.bj |
-0.459 |
0.416 |
1.524 |
|
|
|
.bjJj |
-2.523 |
520.312 |
0.381 |
|
Уменьшим bjJj в семь с половиной раз.
Таблица №4
|
Шаг |
20.5 |
61.5 |
3.075 |
|
|
Мысленные опыты |
|
|
|
|
|
1 |
151.169 |
3818 |
1.28 |
|
|
2 |
150.838 |
3887 |
1.33 |
|
|
3 |
150.506 |
3955 |
1.38 |
|
|
4 |
150.175 |
4023 |
1.43 |
|
|
5 |
149.844 |
4091 |
1.48 |
|
|
|
||||
Вычислим значения параметров оптимизации по линейной модели.
. Таблица №5
|
№ |
X1 |
X2 |
X3 |
|
.y |
|
1 |
-0.06 |
0.055 |
0.2 |
15.961 |
|
|
2 |
-0.12 |
0.109 |
0.4 |
16.316 |
|
|
3 |
-0.181 |
0.164 |
0.6 |
16.672 |
|
|
4 |
-0.241 |
0.219 |
0.8 |
17.027 |
|
|
5 |
-0.301 |
0.273 |
1 |
17.382 |
|
|
|
|
||||
Сравнивая, экспериментальные значения параметра оптимизации и полученные при реализации мысленных опытов нашли, что максимальное значение параметра оптимизации равно у = 17.382, оно получено при значении факторов X1 = 0.428, X2 = 0.253, X3 = 0.4.