СОДЕРЖАНИЕ

Введение 3

1 Моделирование на микроуровне 5

1.1 Исходные данные 5

1.2 Идентификация краевой задачи 5

1.3 Расчет выходной распределенной величины 7

1.4 Расчет интегральной передаточной функции 12

1.5 Построение логарифмической амплитудно-частотной характеристики 15

1.6 Моделирование Elcut 16

2 Моделирование на макроуровне 13

2.1 Исходные данные 13

2.2 Графические формы математической модели гидравлической системы 14

2.3 Матричная форма математической модели 15

2.4 Узловой метод формирования математической модели 17

2.5 Расчет параметров элементов гидросистемы 18

2.6 Расчет статического режима работы гидросистемы 20

2.7 Анализ динамических свойств гидросистемы 23

Заключение 28

Список использованных источников 29

Приложение А 30

ВВЕДЕНИЕ

Моделирование – процесс замещения объекта исследования некоторой его моделью и проведение исследования на этой модели с целью получения необходимой информации об объекте.

Модель – физический или абстрактный образ моделируемого объекта удобного для проведения исследований и позволяющий адекватно отображать интересующие исследователя физические свойства и характеристики объекта.

Различают моделирование предметное и абстрактное.

При предметном моделировании строят физическую модель, которая соответствующим образом отображает физические свойства объекта, при этом объект может иметь иную физическую природу. Недостаток такого вида моделирован - большие временные и материальные затраты.

Абстрактное моделирование связано с построением абстрактной моде (математические соотношения, графы, схемы, диаграммы). Наиболее мощным средством абстрактного моделирования является математическое моделирование.

Математическое моделирование позволяет посредством математических символов и зависимостей составить описание функционирования технического объекта в окружающей внешней среде, определить выходные параметры и характеристики, получить оценку показателей эффективности и качества, осуществить поиск оптимальной структуры и параметров объекта.

Математическая модель - совокупность математических объектов и отношений между ними, адекватно отображающих физические свойства объекта.

В зависимости от степени абстрагирования различают 3 основных иерархических уровня: верхний (меттауровень), средний (макроуровень), нижний (микроуровень).

На макроуровне объект проектирования рассматривают как динамическую систему с сосредоточенными параметрами. Математическая модель макроуровня представляет собой системы обыкновенных дифференциальных уравнений.

На микроуровне объект представляется как сплошная среда с распределенными параметрами. Для описания процесса функционирования таких объектов используют дифференциальные уравнения в частных производных. На микроуровне проектируют неделимые по функциональному признаку элементы технической системы, называемые базовыми элементами (вал, мембрана, стержень).

Целью курсовой работы является синтез интегральной передаточной функции для объектов управления с распределенными параметрами. В данной работе решается вопрос построения математической модели изгиба прямоугольной мембраны на основе теории распределенных сигналов: по заданному дифференциальному уравнению объекта получить выражение для передаточной функции в распределенных параметрах, выражение для выходной величины, выражение для оценочной передаточной функции для наилучших условий управления. Построить оценочную ЛАЧХ, аппроксимировать ее и записать выражение передаточной функции через типовые звенья. Кроме того на макро уровне необходимо исследовать статическую и динамическую модель гидросистемы. Для чего необходимо составить систему дифференциальных уравнений статической модели методом Ньютона, а динамическую модель рассчитать методом Эйлера. В итоге необходимо построить переходный процесс системы.

1 Моделирование на микроуровне

1.1 Исходные данные

Для выполнения первой части курсовой работы примем следующие

исходные данные [1, стр. 101]:

1) Уравнение колебания мембраны:

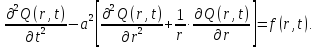
2) Начальные и граничные условия:

;

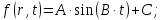
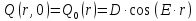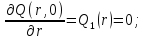
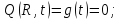
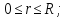
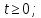
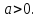
3) Стандартизирующая функция:

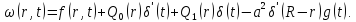
4) Функция Грина:

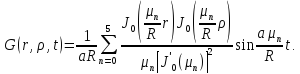
5) Континуальная передаточная функция

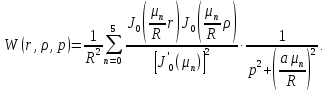
1.2 Идентификация краевой задачи

Уравнение математической физики являются основой для построения математической модели элементов систем управления с распределенными параметрами. Для их практического применения основной сложностью является выбор уравнения, которое могло бы с заданной точностью и степенью достоверности описать интересующий элемент системы.

Колебательные процессы описываются уравнениями гиперболического типа. Рассмотрим двумерную задачу распространения колебаний струны.

Дифференциальное уравнение имеет вид:

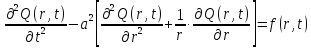(1.1)

где Q(r,t) – выходная величина (колебание мембраны, м);

f(r,t) – входное воздействие на мембрану, м/с²;

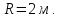
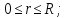
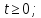
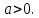
Начальные условия, описывающие прогиб и скорость в начальный момент времени:

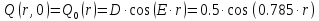
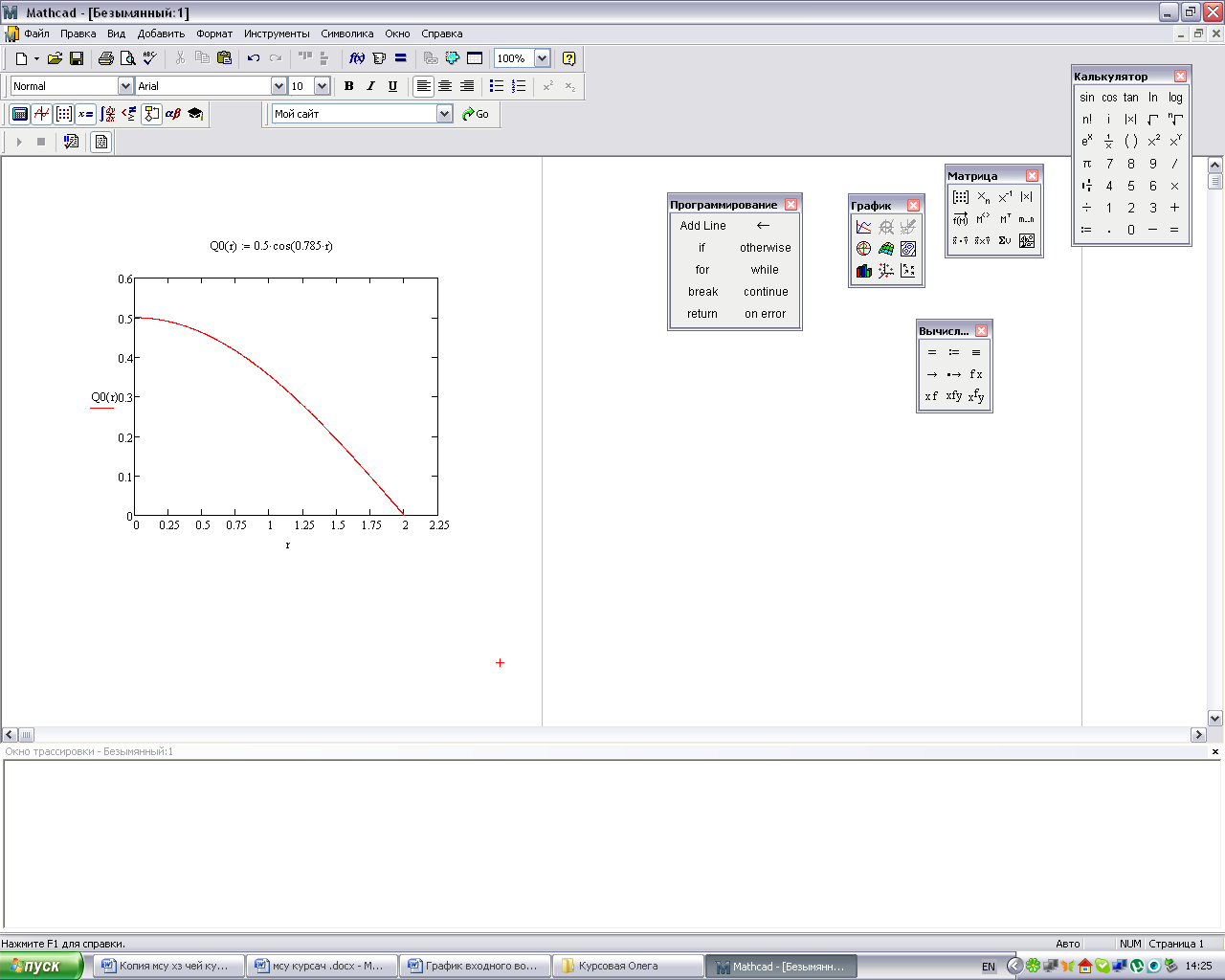
Рисунок 1.1- Начальные условия.

Граничные условия – нулевые, описывающие жесткое закрепление струны по краям:

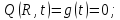
Стандартизирующая функция с учетом принятых условий имеет вид:

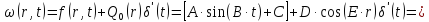
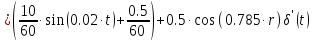(1.2)

Зададим значение волновой скорости мембраны 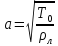м/с.

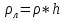-линейная плотность.

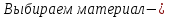резина твердая обыкновенная, плотность которой равна ρ=1,2*10³ [кг/м³], толщина мембраны равна h=0.05[м].

ρ_л=1,2*10³ *0.05=60 [кг/м].

T₀=15 [H].

a=0.5 [м/с].

Входное воздействие, представлено в виде:

.

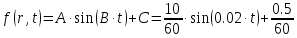Проследим за соблюдением размерности.

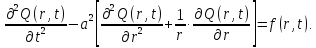
Проверим размерности величин:

Q(r,t)-деформация мембраны, м;

f(r,t)-входное воздействие на мембрану, м/с²;

а – волновая скорость мембраны, м/с.

Учитывая размерности всех коэффициентов и величин, входящих в данное уравнение, получим:

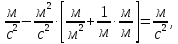
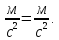
Размерность соблюдается, следовательно, все коэффициенты подобраны верно.

1.3 Расчет выходной распределенной величины

Зная стандартизирующую функцию и функцию Грина, можно найти выходную функцию, вычислением интеграла, представляющий собой основное отношение, связывающее выход объекта при заданном начальном состоянии с входными воздействиями:

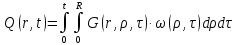(1.3)

В данном случае примем радиус мембраны и время соответственно R=2 м и t=1 c . Вычислим интеграл, связывающий выход объекта при заданном начальном состоянии с выходными воздействиями:

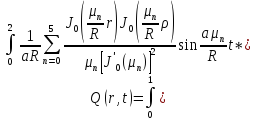
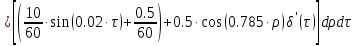(1.4)

Причем

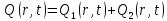
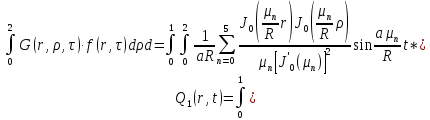
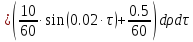
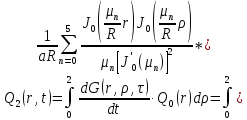
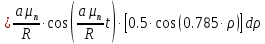
Определим значения 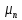как корни уравнения:

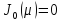
Построим функцию Бесселя

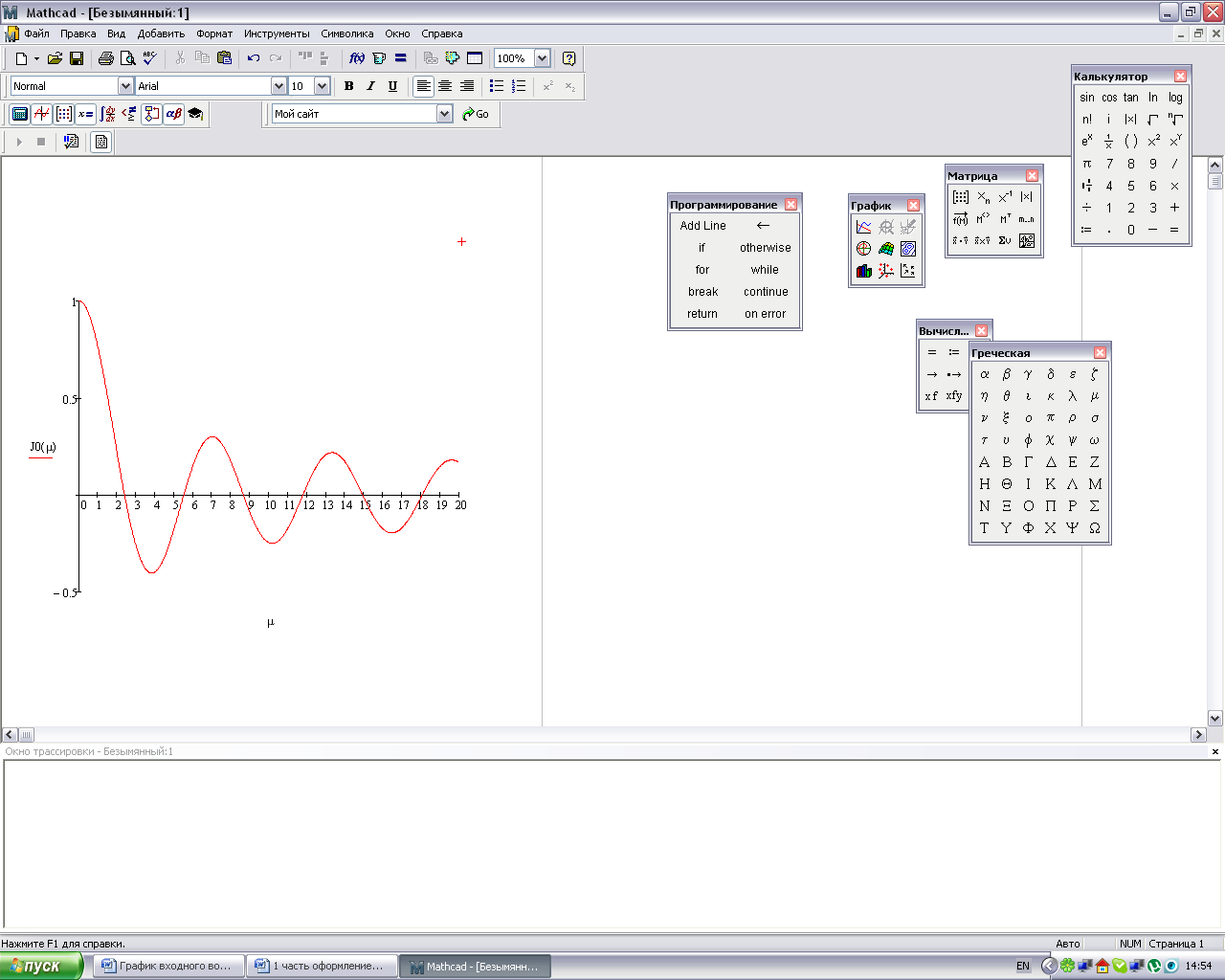
Рисунок 1.2- Функция Бесселя.

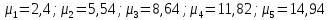
Представим функцию Грина в виде суммы слагаемых:

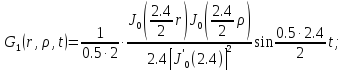
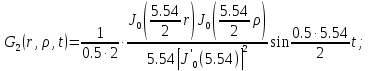
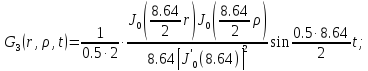
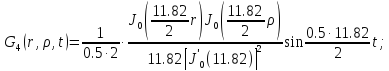
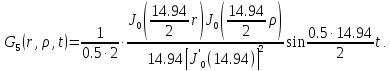
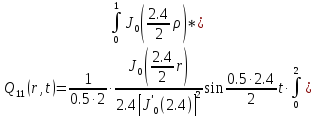
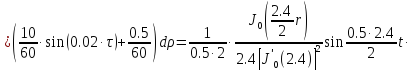
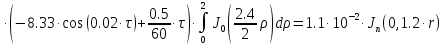
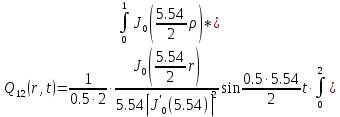
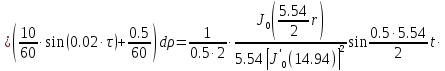
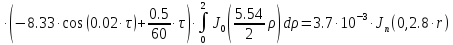
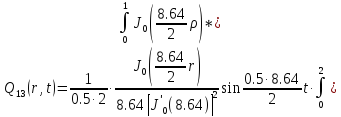
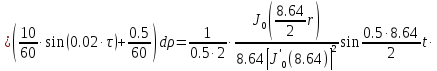
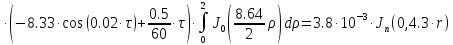
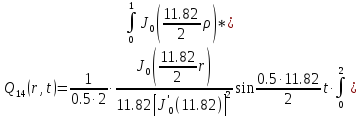
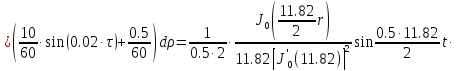
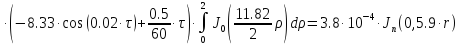
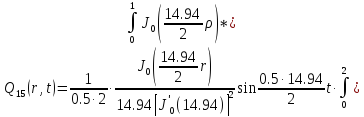
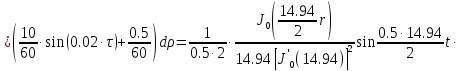
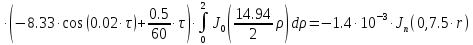
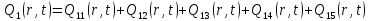
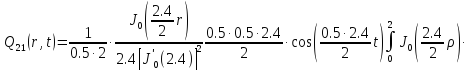
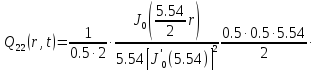
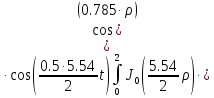
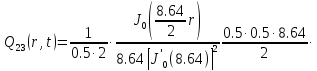
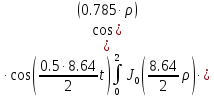
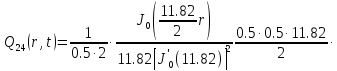
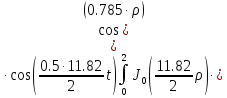
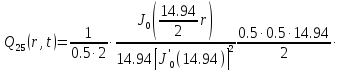
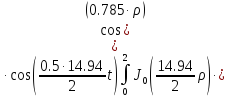
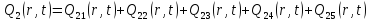
В результате получим уравнение выходной функции состояния объекта с распределенными параметрами:

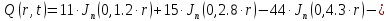
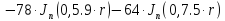(1.5)

Построим функцию колебания мембраны для t=1с и t=50с:

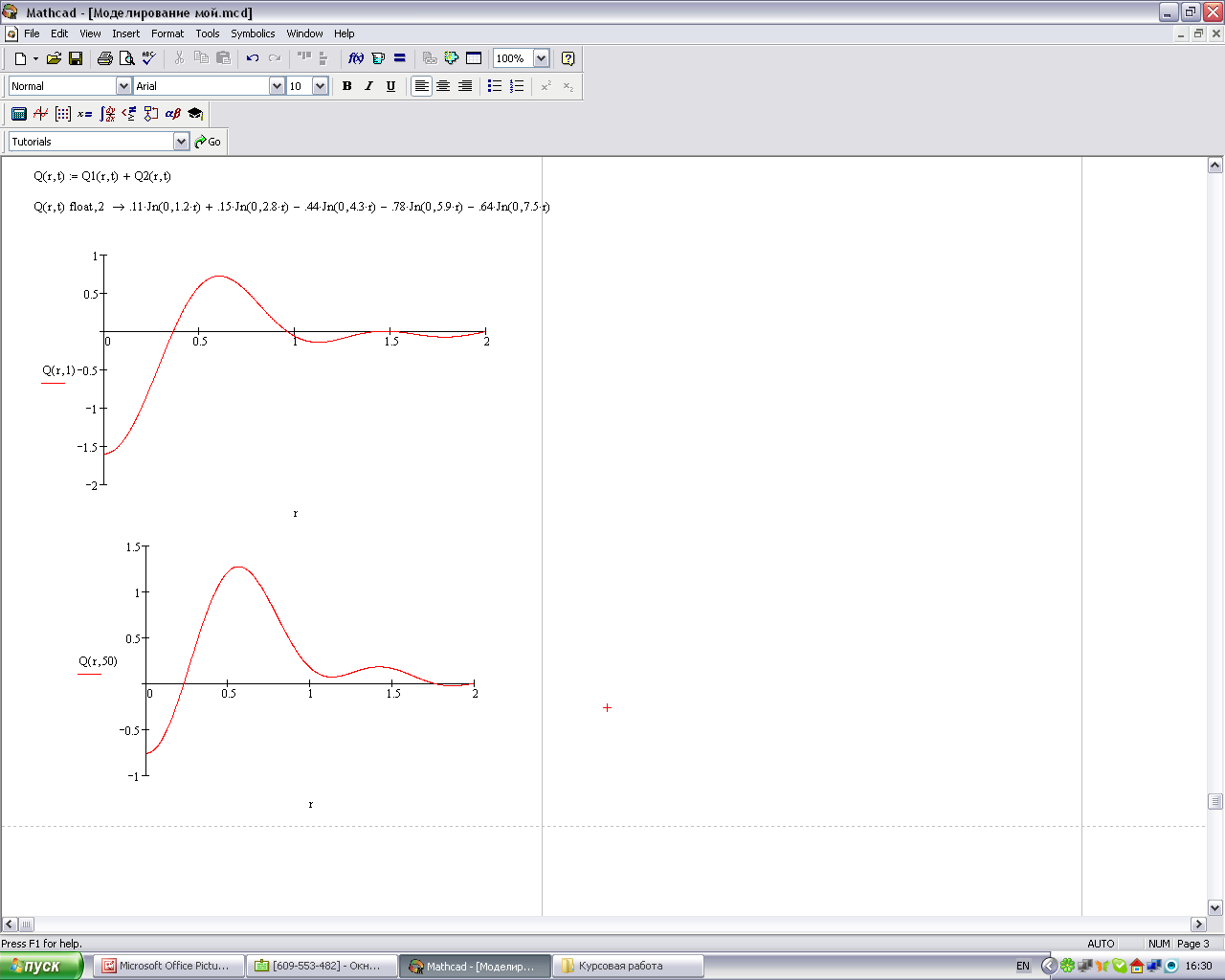
Рисунок 1.3 – График выходной величины Q(x,t) при t=1 c

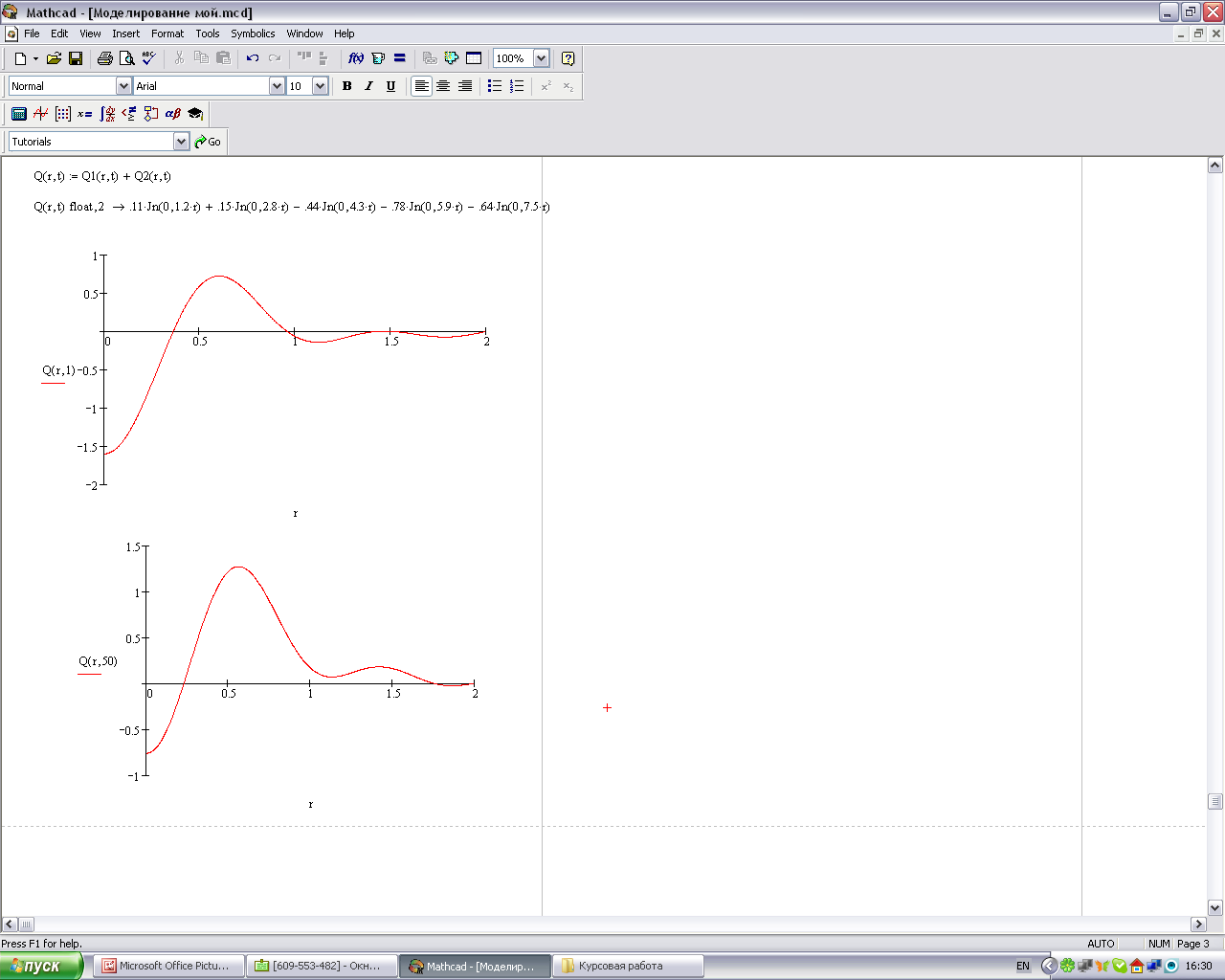
Рисунок 1.4 – График выходной величины Q(x,y,t) при t=50 c

1.4 Расчёт интегральной передаточной функции

По заданному дифференциальному уравнению объекта получим выражение для передаточной функции в распределённых параметрах.

Континуальная передаточная функция имеет вид:

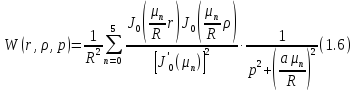
Стандартизирующая функция имеет вид:

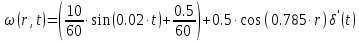
Преобразование по Лапласу стандартизирующей функции:

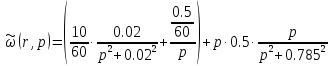(1.7)

Вынесем за скобку входное воздействие, преобразованное по Лапласу:

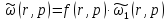
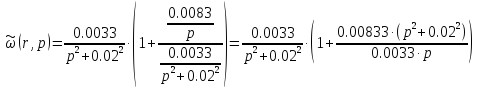
Рассчитаем интегральную передаточную функцию как пространственную композицию от произведения континуальной функции

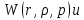
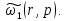
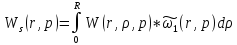(1.8)

Причем

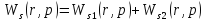
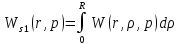
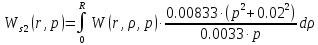
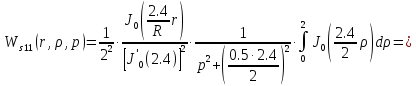
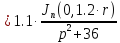
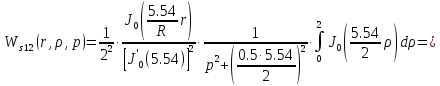
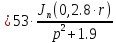
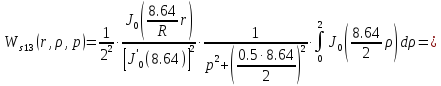
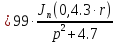
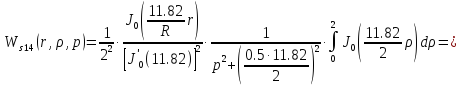
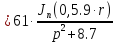
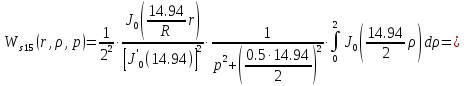
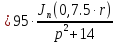
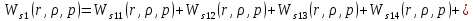
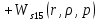
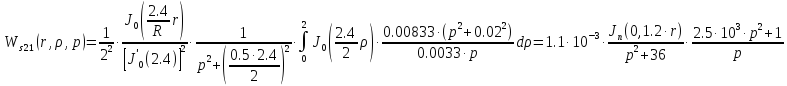
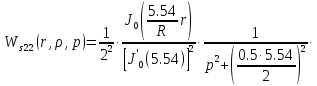
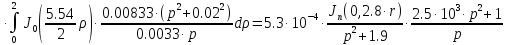
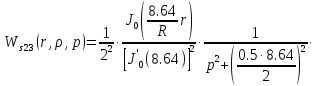
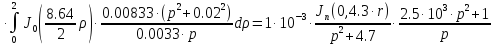
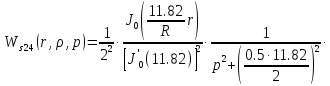
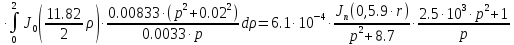
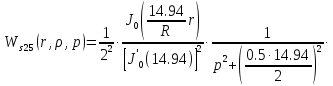
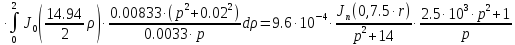
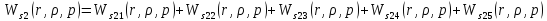
Следовательно получим:

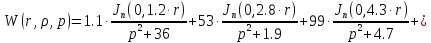
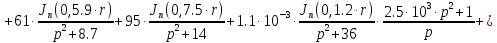
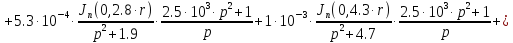
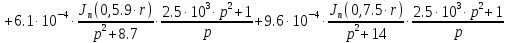
(1.9)

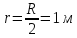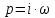Примем и , и получим выражение для частотной передаточной функции:

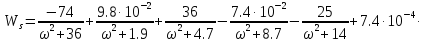
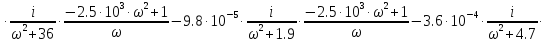
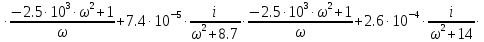
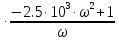(1.10)