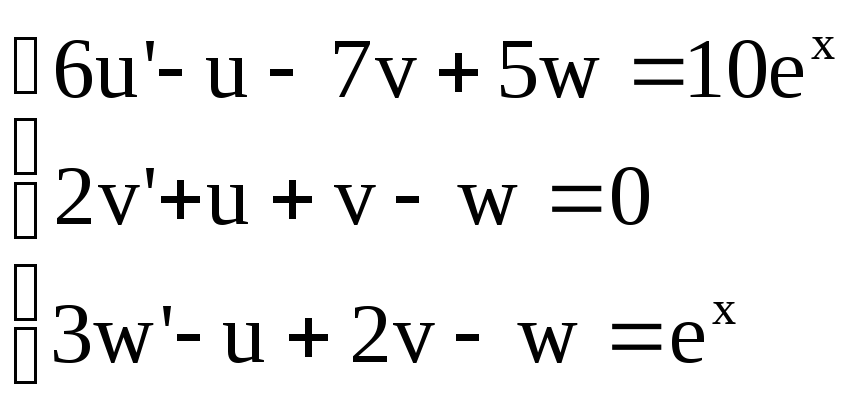- •Системы дифференциальных уравнений
- •1. Основные понятия
- •2. Интегрирование нормальных систем
- •3. Системы линейных дифференциальных уравнений с постоянными коэффициентами
- •Ипользование пакета mathcad при решении систем ду
- •Задания для лабораторной работы
- •Задания для лабораторной работы с ипользованием mathcad
- •Список литературы
Ипользование пакета mathcad при решении систем ду
Системы дифференциальных уравнений, но только первого порядка можно решить с использованием пакета MATHCAD. При этом используется функция rkfixed (y,a,b,N,f) и метод Рунге-Кутты. Ниже приведен пример решения задачи Коши для системы дифференциальных уравнений.
Решите задачу Коши
![]()
![]()
![]()
![]() на отрезке
на отрезке
![]() методом Рунге-Кутты с постоянным шагом
h=0,1. Изобразите графики решений,
вычисленных с шагами
методом Рунге-Кутты с постоянным шагом
h=0,1. Изобразите графики решений,
вычисленных с шагами
![]() .
.
Порядок выполнения задания
-
Установите режим автоматических вычислений.
-
Присвойте переменной ORIGIN значение, равное единице.
-
Присвойте начальное значение решения вектору-столбцу с именем y.
-
Определите правую часть уравнения, присвойте соответствующие выражения элементам вектора-столбца с именем
 .
. -
Найдите величину
 .
. -
Вычислите решение, используя функцию rkfixed(y,a,b,N,f) с параметром N, найденным в п.5.
-
Сохраните решение в матрице
 .
. -
Вычислите решение, используя функцию rkfixed(y,a,b,N,f) с параметром N, найденным по формуле
 .
. -
Сохраните решение в матрице
 .
. -
Вычислите решение, используя функцию rkfixed(y,a,b,N,f) с параметром N, найденным по формуле
 .
. -
Сохраните решение в матрице
 .
. -
Постройте на одном графике все три найденных решения.
-
Оцените погрешности найденных решений по формуле Рунге.
Пример выполнения задания
Решите на отрезке
![]() методом Рунге-Кутты с постоянным шагом
задачу Коши
методом Рунге-Кутты с постоянным шагом
задачу Коши


Оцените погрешности решений, вычисленных с шагами 0,1, 0,05 и изобразите графики приближенных решений. Фрагмент рабочего документа Mathcad с вычислениями и графиками приведен ниже.
![]()
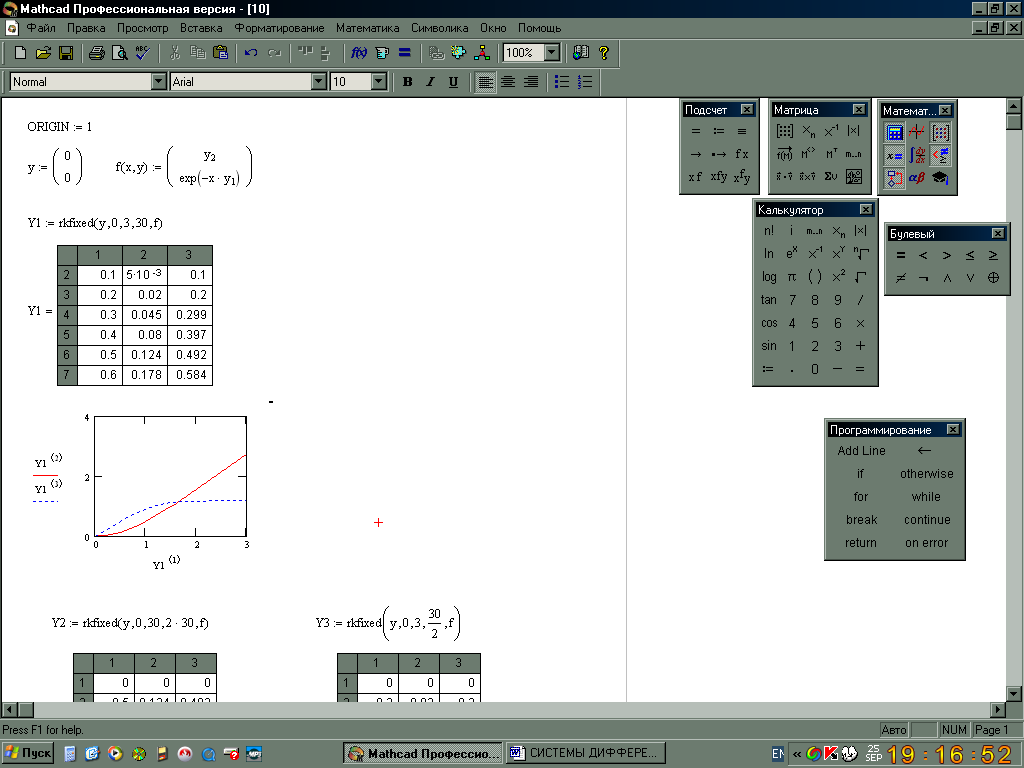
Зададим начальное условие и правые части уравнений системы

Решим задачу Коши
на отрезке
![]() с постоянным шагом h=3/30=0,1
с постоянным шагом h=3/30=0,1
![]()
![]() -
матрица, в первом столбце которой
содержатся значения 30 узлов равномерной
сетки на
-
матрица, в первом столбце которой
содержатся значения 30 узлов равномерной
сетки на
![]() ,
во втором - соответствующие значения
решения y1,
в третьем - значения y2
,
во втором - соответствующие значения
решения y1,
в третьем - значения y2
Выведем таблицу значений решения в узлах равномерной сетки и построим график решения
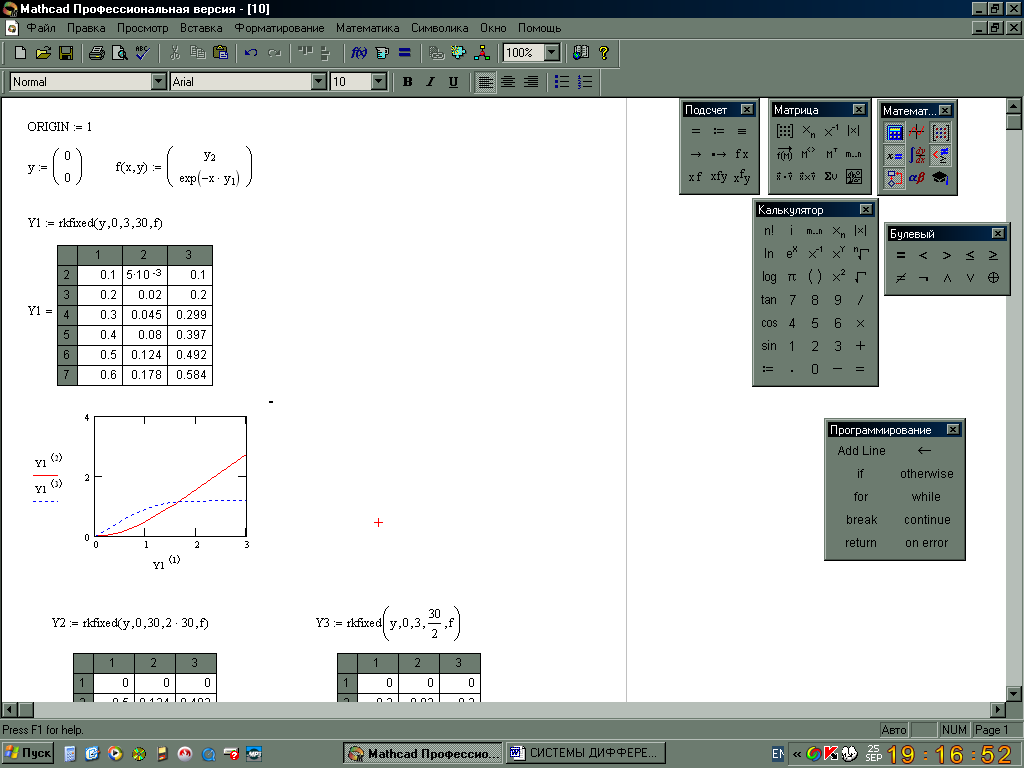
Решим задачу Коши
на отрезке
![]() с постоянным шагом h=3/60=0,05
с постоянным шагом h=3/60=0,05
![]()
![]() -
матрица, в первом столбце которой
содержатся значения 60 узлов равномерной
сетки на
-
матрица, в первом столбце которой
содержатся значения 60 узлов равномерной
сетки на
![]() ,
во втором - соответствующие значения
решения y1,
в третьем - значения y2
,
во втором - соответствующие значения
решения y1,
в третьем - значения y2
Выведем таблицу значений решения в узлах равномерной сетки и построим график решения


Решим задачу Коши
на отрезке
![]() с постоянным шагом h=3/15=0,2
с постоянным шагом h=3/15=0,2
![]()
![]() -
матрица, в первом столбце которой
содержатся значения 15 узлов равномерной
сетки на
-
матрица, в первом столбце которой
содержатся значения 15 узлов равномерной
сетки на
![]() ,
во втором - соответствующие значения
решения y1,
в третьем - значения y2
,
во втором - соответствующие значения
решения y1,
в третьем - значения y2
Выведем таблицу значений решения в узлах равномерной сетки и построим график решения
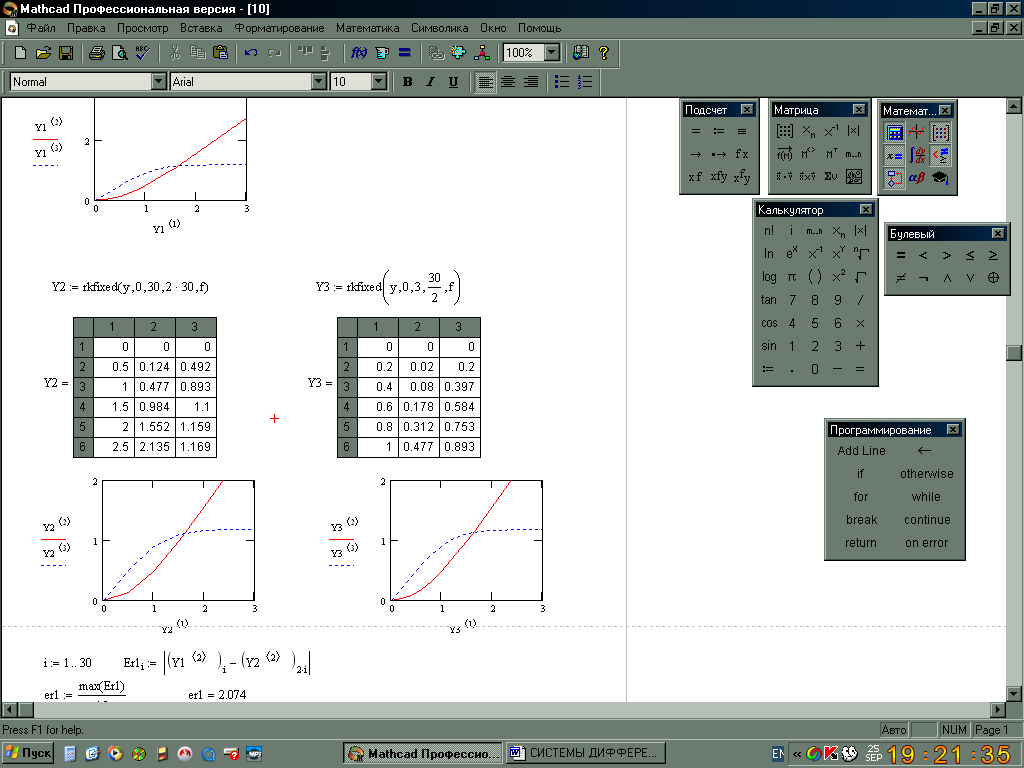
Оценим по Рунге погрешности найденных решений
![]()
![]()
![]()
![]()
Погрешность решения, вычисленного с шагом h=0,05, не превышает 0,01
![]()
![]()
![]()
![]()
Погрешность решения, вычисленного с шагом h=0,1, не превышает 0,01
Задания для лабораторной работы
Найти общее решение системы линейных дифференциальных уравнений с постоянными коэффициентами: