
- •1 Теоретические аспекты информационных технологий. 6
- •2 Сжатие информации 43
- •3 Многоканальная передача и уплотнение линий связи 68
- •Теоретические аспекты информационных технологий.
- •Теория сигналов и спектральный анализ
- •Управление колебаниями
- •Теория информации
- •Дискретизация и квантование.
- •Сжатие информации
- •Адаптивная дискретизация, разностная и дельта-модуляция.
- •Статистическое сжатие.
- •Сжатие динамического диапазона.
- •Эффективное кодирование
- •Модификации кодов Хафмана
- •Алгоритмы Лемпеля – Зива
- •Сжатие графических изображений
- •Видеостандарт mpeg
- •Многоканальная передача и уплотнение линий связи
- •Сравнение и анализ основных методов разделения каналов
- •Адресное разделение каналов.
- •Разделение каналов на основе псевдослучайных последовательностей
- •3.4. Комбинированное разделение каналов
-
Управление колебаниями
Управление колебанием, называемое также модуляцией, - это изменение одного или нескольких его параметров с помощью управляющего воздействия. Исходное колебание называется несущим колебанием или просто несущей; управляющее воздействие - огибающей. Обычно используют два вида несущих: синусоидальную и импульсную. В первом случае модуляция называется непрерывной, во втором - импульсной. При непрерывной модуляции несущая имеет вид U(t)=Usin(t+). Можно независимо изменять амплитуду, частоту или фазу: соответственно имеем амплитудную (АМ), частотную (ЧМ) или фазовую (ФМ) модуляцию:
|
UAM(t)= U[1+aS(t)]cos 0t; |
(1.72) |
|
UЧM(t)= Ucos([0+aS(t)]t+0; |
(1.73) |
|
UФM(t)= Ucos[0t +aS(t)]. |
(1.74) |
Рассмотрим каждый из видов модуляции подробнее. Обычно вначале принимают, что огибающая изменяется по гармоническому закону: S(t) = Scost. После этого рассмотрим S(t) как полигармоническое колебание и случайный процесс.
Амплитудная модуляция (AM). При гармонической огибающей
|
UАМ(t) = U[1+m cost]cos0t, |
(1.75) |
г де
m - индекс (глубина) модуляции. При АМ
0m1;
увеличение m>1 приводит к перемодуляции
и искажениям колебания. На рис. 1.13
показан вид колебания при гармонической
огибающей.
де
m - индекс (глубина) модуляции. При АМ
0m1;
увеличение m>1 приводит к перемодуляции
и искажениям колебания. На рис. 1.13
показан вид колебания при гармонической
огибающей.
Перейдём к рассмотрению спектров. Преобразуем (1.75), раскрыв скобки и преобразовав произведение косинусов:
|
|
(1.76) |
 Как
видно из (1.76), спектр состоит из трёх
составляющих: чистой несущей и двух
боковых компонент, отличающихся по
частоте от несущей. Спектральная
диаграмма, соответствующая этому
случаю, приведена на рис. 1.14,а. Она состоит
из трёх спектральных линий: несущей и
двух боковых (отметим, что всегда 0
>>).
Как
видно из (1.76), спектр состоит из трёх
составляющих: чистой несущей и двух
боковых компонент, отличающихся по
частоте от несущей. Спектральная
диаграмма, соответствующая этому
случаю, приведена на рис. 1.14,а. Она состоит
из трёх спектральных линий: несущей и
двух боковых (отметим, что всегда 0
>>).
При сложной форме огибающей (например, периодическом законе) выражение (1.76) приобретает вид:
|
|
(1.77) |
Здесь mk называются парциальными (частичными) индексами модуляции. Спектр, соответствующий этому колебанию, показан на рис. 1.14,б. На нём обозначено: НБП - нижняя боковая полоса (второй член в (1.77)); ВБП - верхняя боковая полоса; - полоса занимаемых частот. Отсюда следует, что если практическая ширина спектра огибающей ограничивается гармоникой с номером N, то полоса частот при АМ
|
AM = 2N =2в . |
(1.78) |
Это наиболее узкий спектр из всех видов модуляции. Из рис. 1.14,б виден способ построения спектра: каждую спектральную линию огибающей (на чертеже вблизи начала координат) нужно уменьшить вдвое, перенести на оси частот вправо на величину 0, после чего зеркально отразить относительно линии несущей. Если огибающая случайна, мы получим аналогию с узкополосным процессом (см. выше).Несмотря на узкую полосу частот, АМ используется всё реже из-за низкой помехоустойчивости и неэффективной работы приёмопередающей аппаратуры.
Угловая модуляция. Примем сразу, что огибающая гармоническая. Тогда получим следующие выражения для фазовой и частотной модуляций:
|
UФM(t)= Ucos[0t +aScost]; UЧM(t)=
Ucos[0+ |
(1.79) |
Введём
в рассмотрение термин полоса качания:
это максимальный диапазон изменения
полной фазы колебания относительно
её среднего значения. Половина полосы
качания равна индексу модуляции m; она
соответствует множителю перед
гармонической функцией огибающей. Из
соотношений (1.79) видно, что для фазвой
модуляции m = aS, а для частотной m =![]() .
Производная от выражений в квадратных
скобках по частоте огибающей называется
девиацией частоты. Как видно, для
фазовой модуляции Д=m
(пропорциональна частоте огибающей),
а для частотной Д
= aS (не зависит от ).
.
Производная от выражений в квадратных
скобках по частоте огибающей называется
девиацией частоты. Как видно, для
фазовой модуляции Д=m
(пропорциональна частоте огибающей),
а для частотной Д
= aS (не зависит от ).
Особенностью угловой модуляции является то, что индекс модуляции не ограничен сверху: 0<m<. Кроме того, в отличие от АМ, ширина спектра зависит не от спектра огибающей, но в основном от индекса модуляции. Вычисление спектра при угловой модуляции осуществляется через функции Бесселя. Предположим, огибающая синусоидальна, а m>>1. Тогда, используя одно из выражений (1.79) и формулы разложения (1.45), (1.48), можно получить выражение в виде[1.6]:
|
|
(1.80) |
Здесь первый член соответствует несущей, второй и третий - нижняя и верхняя боковые полосы.
Несмотря на то, что в соответствии с (1.80) получается спектр с бесконечной полосой частот, фактически используется особенность функций Бесселя, отмеченная нами ранее: при больших m функции Jк(m) быстро затухают. Практически считают, что значения функций Бесселя при k>m равны нулю, то есть, верхняя и нижняя полосы частот содержат по m спектральных линий, а полная полоса занимаемых частот
|
УM = 2m = Д |
(1.81) |
Как видно из (1.80) и (1.81), даже при синусоидальной огибающей спектр получается достаточно сложным, но зато полоса частот фактически не зависит от формы огибающей (происходит перераспределение амплитуд существующих спектральных линий).Угловая модуляция имеет более высокую помехоустойчивость по сравнению с амплитудной: даже при отсутствии специальных методов повышения помехоустойчивости она в m раз выше [42]. Кроме того, приёмопередающая аппаратура работает всегда в оптимальном режиме, поскольку амплитуда колебаний неизменна.
Если в качестве несущей выбраны прямоугольные импульсы, то при управлении одним из параметров образуются следующие разновидности импульсной модуляции: амплитуда - амплитудно-импульсная (АИМ); длительность - широтно-импульсная (ШИМ); относительное расположение - фазо-импульсная (ФИМ); частота - частотно-импульсная (ЧИМ). Временные диаграммы, иллюстрирующие основные виды модуляций, приведены на рис.1.15.
И мпульсная
модуляция не используется для передачи
на большие расстояния из-за сравнительно
широкого спектра, но часто применяется
в промежуточных преобразованиях.
Например, ШИМ, ЧИМ и ФИМ применяется в
некоторых видах аналого-цифровых
преобразователей, ШИМ– в регуляторах
мощности и импульсных источниках
питания, АИМ- в устройствах выборки-хранения.
мпульсная
модуляция не используется для передачи
на большие расстояния из-за сравнительно
широкого спектра, но часто применяется
в промежуточных преобразованиях.
Например, ШИМ, ЧИМ и ФИМ применяется в
некоторых видах аналого-цифровых
преобразователей, ШИМ– в регуляторах
мощности и импульсных источниках
питания, АИМ- в устройствах выборки-хранения.
 Спектры
импульсно-модулированных колебаний
имеют сложный характер и определяются
в основном спектром несущей и видом
модуляции. При АИМ и гармонической
огибающей спектр имеет вид, приведённый
на рис. 1.16. Видно, что вблизи каждой
спектральной линии несущей, (в том
числе и постоянной составляющей)
появляется по две спектральных линии,
отстоящих от центральной на величину
. Если огибающая
описывается N спектральными линиями, с
обеих сторон от каждой линии несущей
строится этот спектр. При этом
необходимо, чтобы выполнялось условие
N</2,
так как в противном случае на
низкочастотном участке спектра (см.
рис. 1.16 от начала координат до точки
1) произойдёт наложение высокочастотных
участков спектра, что приведёт к
искажению огибающей.
Спектры
импульсно-модулированных колебаний
имеют сложный характер и определяются
в основном спектром несущей и видом
модуляции. При АИМ и гармонической
огибающей спектр имеет вид, приведённый
на рис. 1.16. Видно, что вблизи каждой
спектральной линии несущей, (в том
числе и постоянной составляющей)
появляется по две спектральных линии,
отстоящих от центральной на величину
. Если огибающая
описывается N спектральными линиями, с
обеих сторон от каждой линии несущей
строится этот спектр. При этом
необходимо, чтобы выполнялось условие
N</2,
так как в противном случае на
низкочастотном участке спектра (см.
рис. 1.16 от начала координат до точки
1) произойдёт наложение высокочастотных
участков спектра, что приведёт к
искажению огибающей.
Для других видов модуляции спектр представляется через функции Бесселя и имеет ещё более сложный характер. Подробнее об этом изложено в [10].
Представляет интерес совместное использование непрерывной и импульсной модуляции, а также модуляция непрерывного колебания дискретными сигналами. Особенно интересен второй случай. Результирующие колебания при АМ, ФМ и ЧМ приведены на рис. 1.17.
Вариант АМ в принципе повторяет рассмотренный выше случай, и для скважности Q модулированное колебание имеет вид
|
|
(1.82) |
Обычно практическую ширину спектра определяют по пятую гармонику огибающей [41]; тогда
|
АМ10. |
(1.83) |
Это важная практическая формула для первоначальной оценки требуемой полосы частот.
П ри
частотной модуляции (см. рис. 1.17)
используют двухчастотный метод, при
котором уровень "0" передаётся на
частоте 0, а
уровень "1"-на частоте 1.
При определении спектра можно
использовать принцип суперпозиции:
сигнал UЧМ(t) представить в виде
суммы двух амплитудно-модулированных
колебаний с частотами 0
и 1. Тогда на
основании (1.82)
ри
частотной модуляции (см. рис. 1.17)
используют двухчастотный метод, при
котором уровень "0" передаётся на
частоте 0, а
уровень "1"-на частоте 1.
При определении спектра можно
использовать принцип суперпозиции:
сигнал UЧМ(t) представить в виде
суммы двух амплитудно-модулированных
колебаний с частотами 0
и 1. Тогда на
основании (1.82)
|
|
(1.84) |
С пектр,
построенный по соотношению (1.84), показан
на рис. 1.18. Здесь З
- полоса запаса, предназначенная для
более надёжного разделения 0 и 1 при
приёме. Если, как и в предыдущем
случае, ограничить спектр огибающей по
пятую гармонику и считать З
= 0, то полоса занимаемых частот:
пектр,
построенный по соотношению (1.84), показан
на рис. 1.18. Здесь З
- полоса запаса, предназначенная для
более надёжного разделения 0 и 1 при
приёме. Если, как и в предыдущем
случае, ограничить спектр огибающей по
пятую гармонику и считать З
= 0, то полоса занимаемых частот:
|
ЧМ20. |
(1.85) |
Фазовая модуляция при дискретной огибающей приводит к тому, что несущая претерпевает скачки фазы в моменты перехода огибающей из 1 в 0 и наоборот (см. рис. 1.17). При этом у ФМ появляется замечательное свойство: если скачки фазы составляют 180, спектр ФМ колебания совпадают со спектром АМ с подавленной несущей:
|
|
(1.86) |
Спектральная диаграмма приведена на рис. 1.19; штриховой линией показано место расположения отсутствующей несущей. По аналогии с (1.83)
|
ФМ =АМ10. |
(1.87) |
Е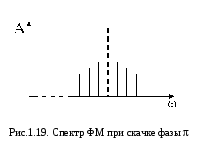 сли
учесть повышенную помехоустойчивость
фазомодулированных колебаний, особенно
при использовании специальных методов
приёма, то становится очевидным
широкое использование ФМ в практике
передачи дискретных сигналов. Плата за
это - возможная инверсия сообщений -
приёмник воспринимает скачок фазы как
переход из 0 в 1 и наоборот, а так как
оба перехода тождественны, то при
неправильном приёме одного скачка
дальнейшая информация воспринимается
в инверсной форме. Более подробно об
этом эффекте и способах борьбы с ним
будет изложено в следующем разделе.
сли
учесть повышенную помехоустойчивость
фазомодулированных колебаний, особенно
при использовании специальных методов
приёма, то становится очевидным
широкое использование ФМ в практике
передачи дискретных сигналов. Плата за
это - возможная инверсия сообщений -
приёмник воспринимает скачок фазы как
переход из 0 в 1 и наоборот, а так как
оба перехода тождественны, то при
неправильном приёме одного скачка
дальнейшая информация воспринимается
в инверсной форме. Более подробно об
этом эффекте и способах борьбы с ним
будет изложено в следующем разделе.

