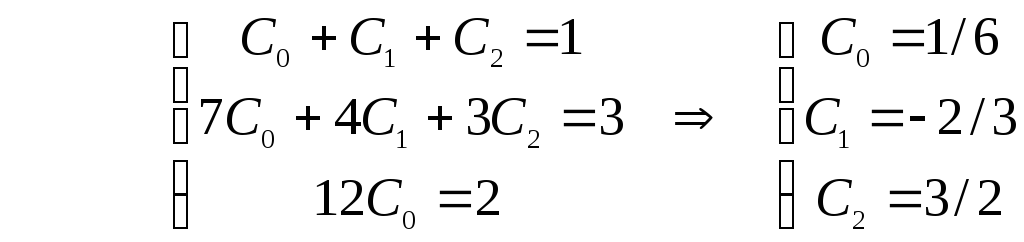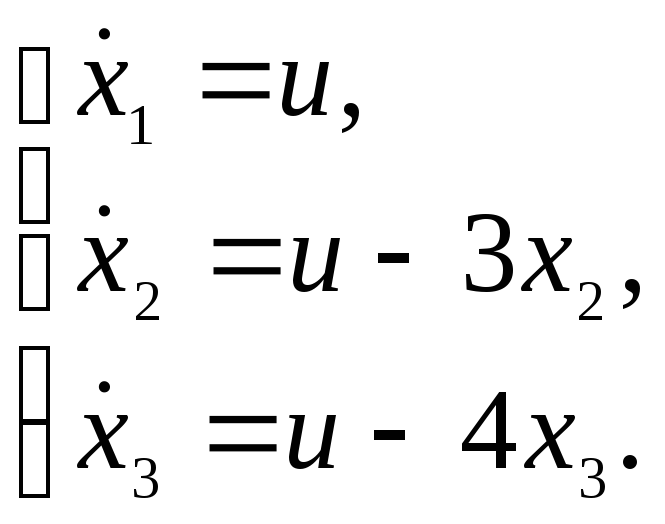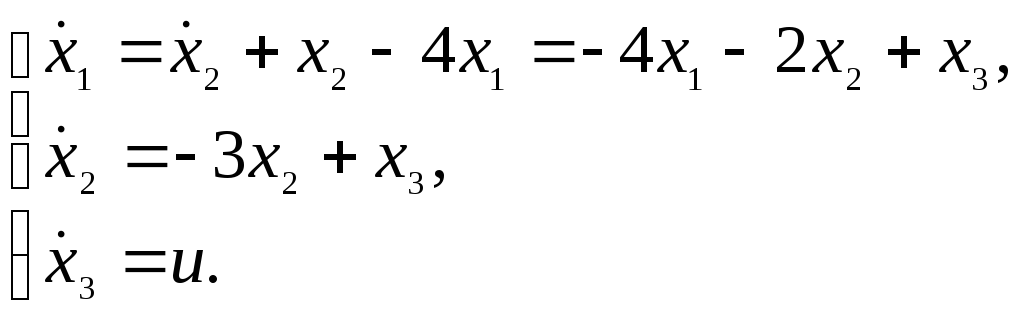Министерство образования и науки Российской федерации

Федеральное агентство по образованию

Саратовский государственный технический университет

Балаковский институт, техники, технологии и управления

Разработка моделей систем управления в пространстве состояний с использованием схем моделирования

Методические указания к выполнению практической работы

по дисциплине «Моделирование систем» для студентов специальности 220201 «Управление и информатика в технических системах» всех форм обучения

Одобрено

редакционно-издательским советом

Балаковского института техники,

технологии и управления

Балаково 2010

ВВЕДЕНИЕ

При моделировании систем управления методами современной теории управления модель задается в переменных состояниях. При этом по сравнению с традиционными моделями (передаточные функции, частотные характеристики и т.д.) эти модели имеют следующие преимущества:

- кроме двух внешних переменных (входной и выходной) в модели отражаются и все внутренние переменные системы;

- наличие информации о внутренних переменных позволяет более эффективно осуществлять процедуру проектирования системы;

- для систем высокого порядка модели легко разрешимы с помощью компьютера и др.[1].

Модель системы в переменных состояния можно получить двумя путями: используя дифференциальные уравнения и используя схемы моделирования. Свое название схемы моделирования получили потому, что они представляют собой «заготовку» для исследования системы с помощью аналоговых или цифровых компьютеров. Наиболее часто схемы моделирования реализуются способами прямого, параллельного и последовательного программирования.

Цель работы - изучение схем моделирования систем управления с помощью описанных способов программирования и разработка с их помощью моделей в пространстве состояний.

Основные теоретические сведения

Общий принцип построения схем моделирования заключается в формировании структурной схемы, состоящей только из интеграторов, сумматоров и коэффициентов усиления. Заметим, что если схема моделирования строится на основе дифференциальных уравнений, то структурная схема является однозначной, т.е. однозначно определяет все фазовые координаты системы. Если исходные данные представлены в виде передаточных функций, то схемы моделирования могут иметь разные структуры (способы прямого, параллельного и последовательного программирования), которые приводят к неоднозначному представлению фазовых координат системы. Причем, многообразие представления фазовых координат системы не изменяет выходных сигналов этой системы.

Также существуют понятия схем моделирования, называемых канонической формой управляемости и канонической формой наблюдаемости [1]. В данной работе метод прямого программирования и есть метод, приводящий к построению схемы моделирования в канонической форме управляемости.

Основным элементом схемы моделирования является интегратор. Если выход интегратора обозначить через y(t), то его входом должна быть первая производная dy(t)/dt. Рассмотрим последовательное соединение двух интеграторов (рис.1). Если выход второго интегратора обозначить через , то его входом должна быть первая производная dy(t)/dt; аналогично входом первого интегратора должна быть вторая производная. Цепочку из последовательно соединенных n интеграторов можно использовать для моделирования систем n порядка.

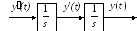
Рис.1. Структурная схема моделирования двух последовательно соединенных

интеграторов

Рассмотрим составление схемы моделирования на основе дифференциальных уравнений на примере механической системы с линейным перемещением y(t) (рис.2). На тело массой M действуют три силы – внешняя сила f(t), сила трения, пропорциональная скорости, – , сила упругости, пропорциональная перемещению, – .

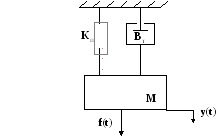
Рис.2. Механическая система с линейным перемещением

Под действием этих сил тело движется согласно закону Ньютона, который гласит, что сумма сил, действующих на тело, равна произведению массы тела на его ускорение. Дифференциальное уравнение, описывающее движение системы, имеет вид:

.

(1)

На рис.3 представлена схема моделирования механической системы.

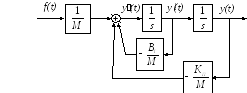
Рис.3.Структурная схема механической системы, описываемой уравнением (2)

Входом двух интеграторов является вторая производная и уравнение механической системы (1) принимает вид:

.

(2)

Следовательно, чтобы связать все переменные, входящие в уравнение (2), схему рис.1 нужно дополнить сумматором и тремя коэффициентами усиления.

Рассмотрим способы построения схем моделирования по передаточным функциям. Классическая форма представления математической модели – это описание системы регулирования с помощью дифференциального уравнения

.

(3)

или операторного уравнения

,

(4)

где , – входной и выходной сигналы системы регулирования;

, – изображение входного и выходного сигналов.

Используя выражение (4), определяется передаточная функция

.

(5)

Пусть передаточная функция системы имеет вид:

.

(6)

Разделив числитель и знаменатель на , получим

.

(7)

Выходная величина может быть выражена следующим образом:

,

(8)

где .

Отсюда следует, что

.

(9)

Из приведенных выражений ясно, что схема переменных состояния должна содержать n последовательно включенных интегрирующих звеньев, выходные величины которых с соответствующими коэффициентами , складываются с входным сигналом и уменьшаются в , образуя сигнал ошибки .

Далее сигнал , усиленный в раз, суммируется с выходными величинами интеграторов, взятыми с коэффициентами , образуя выходную величину . Полученная таким образом схема приведена на рис.4.

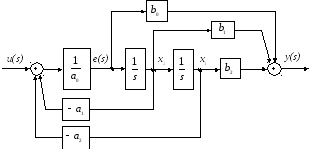
Рис.4. Схема моделирования системы по методу прямого программирования

При параллельном программировании передаточную функцию предварительно раскладывают на элементарные дроби. Для этого должны быть известны корни характеристического уравнения знаменателя ПФ:

(10)

где корни характеристического уравнения знаменателя передаточной функции , коэффициенты и определяются по формуле [4]:

,

(11)

Следует указать, что появится только тогда, когда степень полинома числителя равна степени полинома знаменателя, если полином числителя имеет меньшую степень, то , что выполняется для всех систем регулирования, состоящих из инерционных звеньев, схема моделирования по методу параллельного программирования приобретает вид, представленный на рис.5.

Рис.5. Схема моделирования для параллельного программирования

Для построения схем моделирования способом последовательного программирования передаточная функция должна быть представлена в виде последовательного соединения элементарных звеньев с передаточными функциями вида:

;

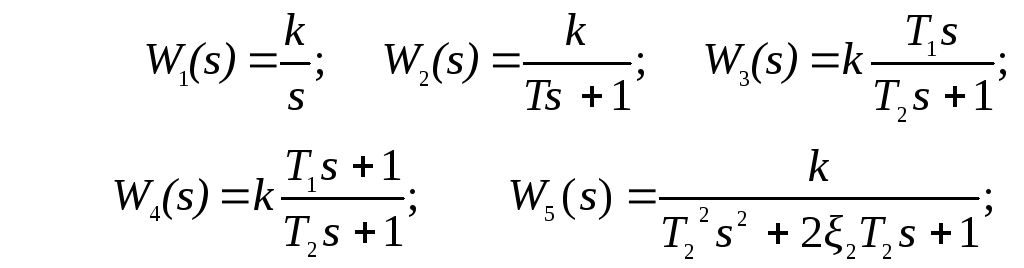
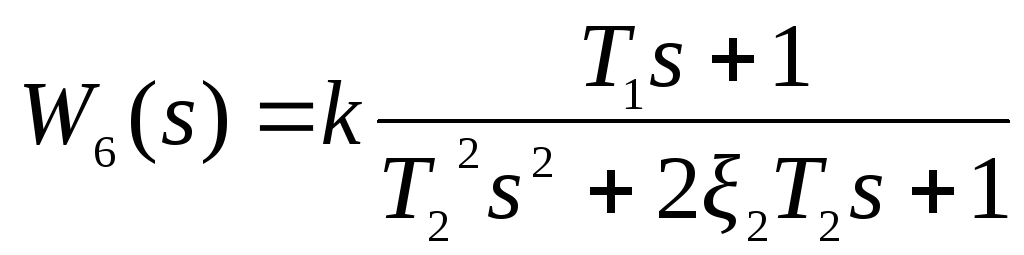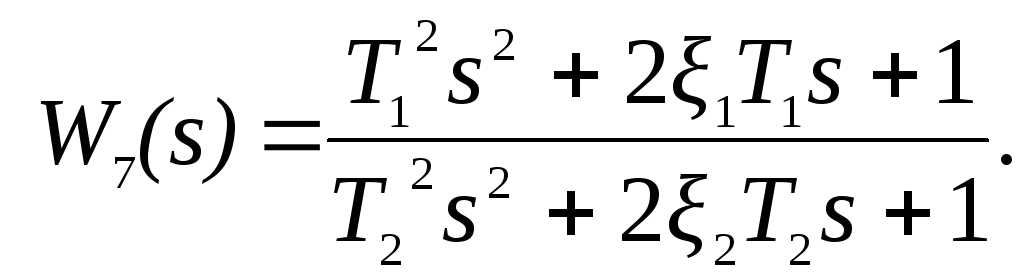
Для каждой из этих передаточных функций на основе метода прямого программирования разработаны схемы в переменных состояния [2]. Эти схемы представлены на рисунках 6-12.

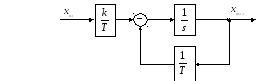
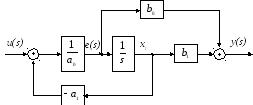
Рис.6. Схема моделирования для интегрирующего звена c передаточной функцией W1

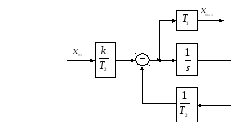
Рис.7. Схема моделирования для апериодического звена c передаточной функцией W2

Рис.8. Схема моделирования для реального дифференцирующего звена c передаточной функцией W3

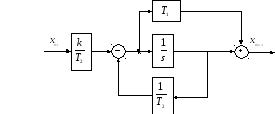
Рис.9. Схема моделирования для упругого звена c передаточной функцией W4

Рис.10. Схема моделирования для колебательного звена c передаточной функцией W5

Рис.11. Схема моделирования для звена с передаточной функцией

Структурные схемы передаточных функций, образованных полиномами первой и второй степени, изображены на рис.13, 14.

; .

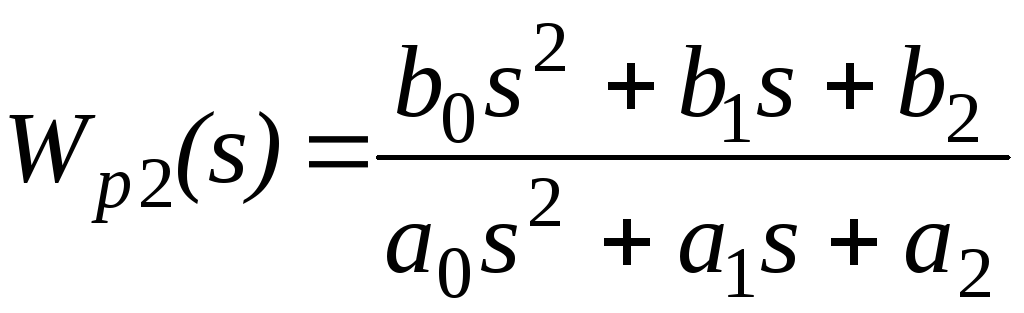Например, для передаточной функции:

(12)

схема моделирования, полученная методом последовательного программирования, изображена на рис.15.

Рис.12. Схема моделирования для звена с передаточной функцией

Рис.13. Схема моделирования для звена с передаточной функцией

Рис.14. Схема моделирования для звена с передаточной функцией

Рис.15. Схема моделирования передаточной функцией (12)

Описанные выше схемы моделирования предназначены для получения моделей в пространстве состояний. Стандартная форма уравнения в пространстве состояний линейной стационарной непрерывной системы имеет вид [1]:

; .

(13)

В этих уравнениях:

- вектор состояния размерности (), компонентами которого являются переменные состояния системы n-го порядка;

- вектор производной по времени от вектора ;

- матрица коэффициентов системы ();

- матрица входа ();

- вектор входа размерности (), компонентами которого являются входные переменные системы;

- вектор входа размерности (), компонентами которого являются выходные переменные системы;

- матрица выхода ();

- матрица обхода, определяющая прямую зависимость выхода от входа.

Способ записи моделей в пространстве состояний вида (13) для каждой из схем моделирования рассмотрен в примере выполнения задания.

Выбор способа построения схемы переменных состояния в каждом конкретном случае определяется сложностью передаточной функции системы, а также требованиями, предъявляемыми к расчету системы.

Например, способ прямого программирования целесообразно применять в тех случаях, когда передаточная функция системы имеет высокий порядок и разложение на элементарные дроби затруднено.

Когда же необходимо определить не только выходную величину, но и другие переменные (скорость, ток и т.д.), которые соответствуют переменным физической системы, то целесообразно применять способ последовательного программирования. При этом способе моделирования фазовые координаты модели и физически реализуемой системы совпадают.

При теоретических исследованиях целесообразно применять метод параллельного программирования. В этом случае матрица принимает наиболее простой (диагональный) вид, так как все координаты развязаны. Следует отметить, что при комплексных корнях системы регулирования в матрице коэффициентов и в матрице управления появятся комплексные числа, что затрудняет применение метода параллельного программирования.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. По заданной передаточной функции методом прямого программирования составить схему моделирования и определить численные значения матриц коэффициентов модели в пространстве состояний.

2. По заданной передаточной функции методом параллельного программирования составить схему моделирования и определить численные значения матриц коэффициентов модели в пространстве состояний.

3. По заданной передаточной функции методом последовательного программирования составить схему моделирования и определить численные значения матриц коэффициентов модели в пространстве состояний.

ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ

Рассмотрим систему с передаточной функцией вида:

.

(14)

1. Рассмотрим получение схемы моделирования системы методом прямого программирования. Определим выходную величину , используя нижеприведенные обозначения:

; .

(15) (16)

Уравнение (16) разрешим относительно старшей производной

; .

(17)

По уравнению (17) составим схему моделирования (рис.16).

Выходная величина системы получается из уравнения (15) как линейная комбинация фазовых координат.

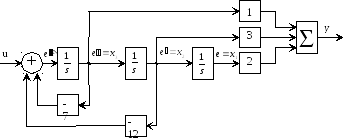
Рис.16. Схема моделирования системы методом прямого программирования

Из схемы моделирования можно записать дифференциальное уравнение (3) в форме Коши (18). Так как впоследствии системы регулирования будут описываться матричными уравнениями (форма пространства состояния), то используем стандартные обозначения. Фазовую координату интегратора, стоящего на выходе, обозначим , (), предыдущего - , () и т. д. С учетом этих замечаний фазовые координаты схемы моделирования (см. рис.16) связаны следующими соотношениями:

; ; .

(18)

Выходная величина определяется как линейная комбинация фазовых координат (15)

.

(19)

Из схемы моделирования (см. рис.16) или системы уравнений (18) и (19) получим матрицы коэффициентов , В, и D:

.

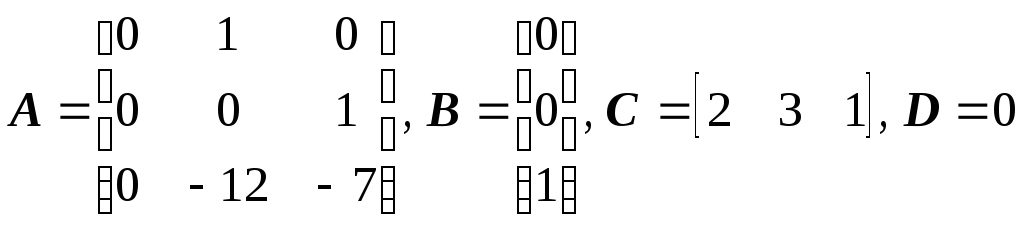2. Рассмотрим получение схемы моделирования системы методом параллельного программирования. Схема для параллельного программирования получается из передаточной функции (14), если ее представить в виде суммы элементарных дробей. Разложение на элементарные дроби выполним с помощью метода неопределенных коэффициентов [4]:

.	(20)
	(21)

Могут быть использованы и другие методы разложения на элементарные дроби, например, метод Хевисайда [4]. В пакете MatLab корни знаменателя и коэффициенты с помощью данного метода по формулам (11) определяются следующей программой:

coef = [1, 7, 12, 0]; % Задание коэффициентов многочлена

r = roots (coef) % Определение корней многочлена

(результат вычислений: r = 0 -4 -3)

syms p % Описание переменной

C0=limit([(p^2+3*p+2)*p/(p^3+7*p^2+12*p)],0) % Определение предела

функции в точке p=0.

C1=limit([(p^2+3*p+2)*(p+3)/(p^3+7*p^2+12*p)],-3) % Определение предела

функции в точке p=-3.

C2=limit([(p^2+3*p+2)*(p+4)/(p^3+7*p^2+12*p)],-4) % Определение предела

функции в точке p=-4.

(результат вычислений: C0 = 1/6 C1 = -2/3 C2 = 3/2).

С учетом численных значений коэффициентов (21) по выражению (20) запишем передаточную функцию в виде суммы элементарных звеньев:

.

(22)

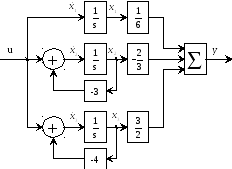
Тогда схема моделирования методом параллельного программирования имеет вид, представленный на рис.17.

На основании схемы моделирования (рис.17) составим дифференциальные уравнения системы в переменных состояния для параллельного программирования:

(23)

Выход является, как и ранее, линейной комбинацией координат , и :

.

(24)

Рис.17. Схема моделирования системы методом параллельного программирования

Из схемы моделирования (см. рис.17) или уравнений (23), (24) получаем матрицы коэффициентов А, В, С, D:

.

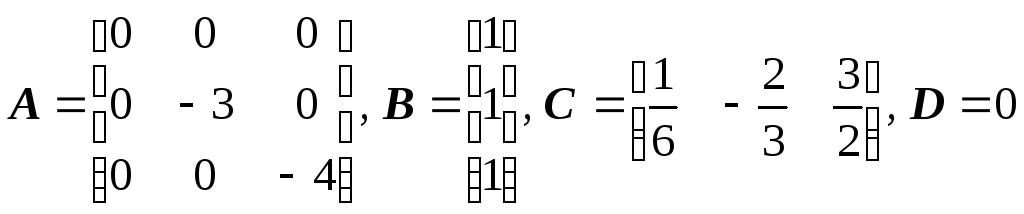3. Рассмотрим получение схемы моделирования системы методом последовательного программирования. Схема для последовательного программирования получается из передаточной функции (14), если ее разбить на блоки и для каждого блока представить схему моделирования:

.	(25)
По передаточной функции (22) составляем схему (рис.18).

Система дифференциальных уравнений первого порядка, записанная на основании схемы рис.18, имеет вид:

	(26)
Рис.18. Схема моделирования системы методом последовательного программирования

Выход определяется линейной комбинацией фазовых координат:

.

(27)

Матрицы коэффициентов , , , данной системы:

.

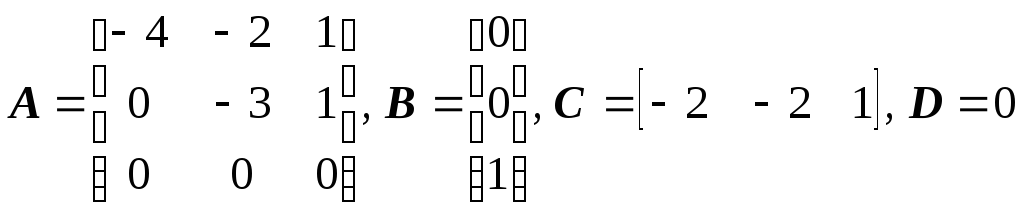Таким образом, на основании исходной модели системы в виде передаточной функции составлены три схемы моделирования, на основании которых записаны модели системы в пространстве состояний. Схемы моделирования имеют разные структуры и приводят к различным моделям в пространстве состояний.

ВАРИАНТЫ ЗАДАНИЙ

№ п/п	Передаточная функция исследуемой системы	№ п/п	Передаточная функция исследуемой системы
1	2	3	4
1		13
2		14

1	2	3	4
3		15
4		16
5		17
6		18
7		19
8		20
9		21
10		22
11		23
12		24
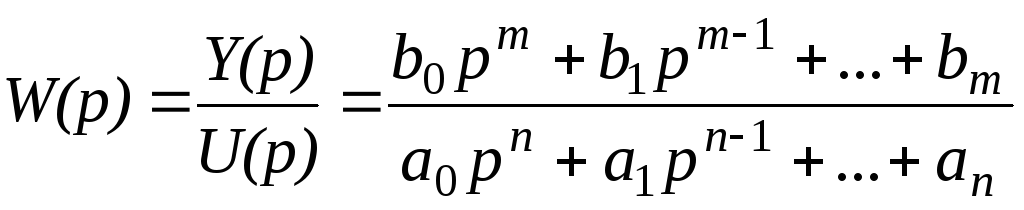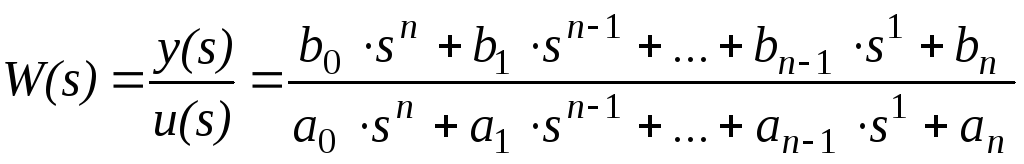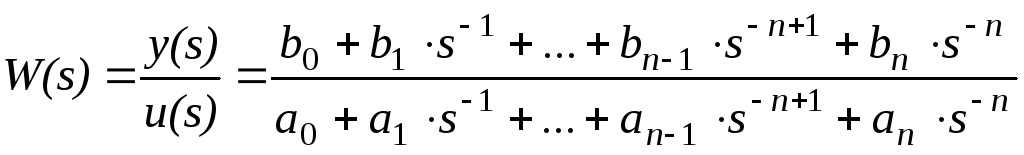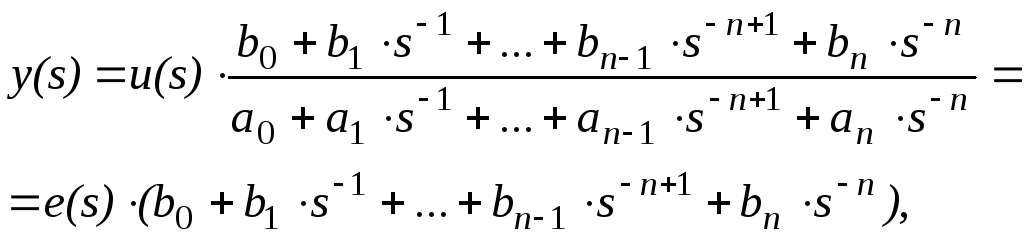
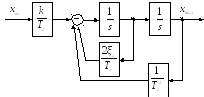
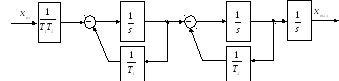
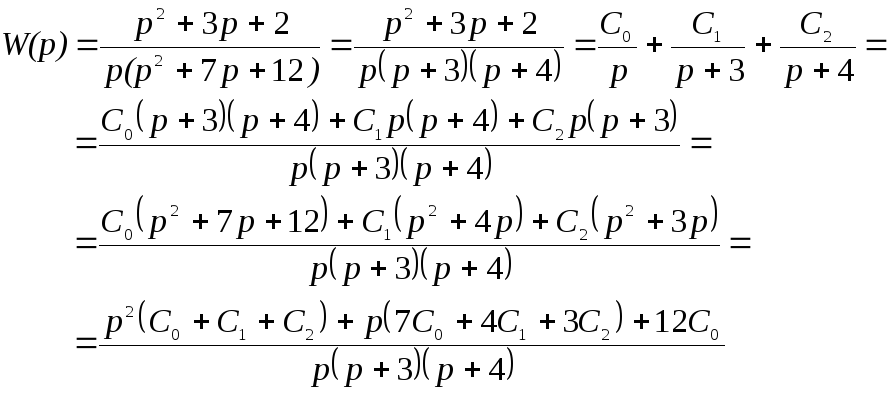