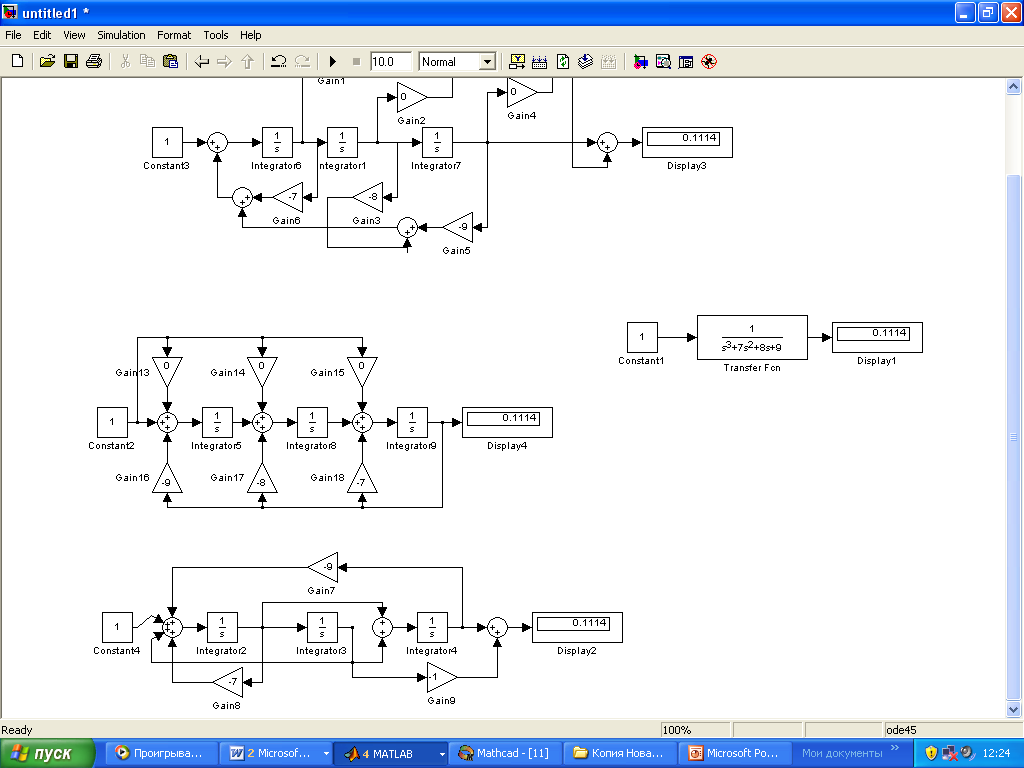
- •Разработка моделей систем управления в пространстве состояний с использованием преобразований подобия
- •Преобразованные матрицы новой системы координат вычисляются по формулам:
- •Разработка моделей систем управления в пространстве состояний с использованием преобразований подобия
- •Составила: Мефедова Юлия Александровна Рецензент т.Н. Скоробогатова Редактор л.В.Максимова
Министерство образования и науки Российской федерации
Федеральное агентство по образованию
Саратовский государственный технический университет
Балаковский институт, техники, технологии и управления
Разработка моделей систем управления в пространстве состояний с использованием преобразований подобия
Методические указания к выполнению практической работы
по дисциплине «Моделирование систем» для студентов специальности 220201 «Управление и информатика в технических системах» всех форм обучения
Одобрено
редакционно-издательским советом
Балаковского института техники,
технологии и управления
Балаково 2010
ВВЕДЕНИЕ
Системы управления
с одним входом и одним выходом
характе-ризуются внешними и внутренними
характеристиками. Внешние характеристики
однозначны. Это передаточные функции
и диффе-ренциальные уравнения. Количество
внутренних характеристик (моделей
состояния) неограниченно. Ранее изучены
три схемы моделирования, характеризующиеся
своими матрицами
![]() ,
,
![]() ,
,
![]() .
В действительности для характеристики
одной и той же системы можно предложить
не-ограниченное количество матриц
.
В действительности для характеристики
одной и той же системы можно предложить
не-ограниченное количество матриц
![]() ,
,
![]() ,
,
![]() ,
каждой из которых будет соответствовать
модель в переменных состояния. Выбор
той или иной модели обусловлен:
,
каждой из которых будет соответствовать
модель в переменных состояния. Выбор
той или иной модели обусловлен:
- необходимостью иметь в качестве переменных состояния естественные физические величины (скорость, положение, ток и т.д.), что позволяет перенести результаты моделирования на физическую модель без предварительных преобразований;
- необходимостью облегчить синтез системы управления;
- необходимостью формализировать процесс расчета.
Таким образом, существуют такие преобразования подобия, которые изменяют внутреннюю структуру системы (модель состояния), но не из-меняют соотношение между входом и выходом системы (передаточную функцию).
Цель работы - изучение методов применения теории подобия при разработке моделей систем управления в пространстве состояний.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Преобразования подобия часто используются в современной теории управления, так как приходится определять различные характеристики систем в разных базисах. Модель системы в пространстве состояний:
|
|
(1) |
Введем невырожденное линейное преобразование:
|
|
(2) |
где ![]() -
вектор состояния системы в новом базисе;
-
вектор состояния системы в новом базисе;
![]() - произвольная
невырожденная матрица.
- произвольная
невырожденная матрица.
Невырожденность матрицы определяется ее рангом или определителем. Для невырожденной матрицы ранг должен быть равен степени характеристического уравнения, или её определитель не должен быть равен нулю.
Для перехода к
новому базису умножим первое уравнение
системы (1) на
![]() ,
а затем значение
,
а затем значение
![]() из (2) подставим в систему (1):
из (2) подставим в систему (1):
|
|
(3) |
В новых переменных уравнение системы принимает вид:
|
|
(4) |
Преобразованные матрицы новой системы координат вычисляются по формулам:
|
|
(5) |
Матрицы, связанные последним соотношением, определяются как подобные. У этих матриц равны характеристические многочлены, определители и собственные значения. Передаточные функции, связывающие выходные сигналы с входными сигналами, у подобных матриц также одинаковы.
Для конкретной системы можно предложить неограниченное количество моделей в переменных состояния. Желательно так выбрать базис, чтобы матрицы были "удобны", т.е. их легко можно было получить, их удобно использовать при доказательстве теорем, с их помощью просто создать схемы моделирования, а, главное, результаты моделирования просто переносить на физическую модель. Этим требованиям удовлетворяют модели, созданные в базисах:
- управляемое каноническое представление (УКП);
- идентификационное каноническое представление (ИКП).
Запись матриц в форме УКП осуществляется относительно просто по дифференциальному уравнению, характеристическому уравнению или передаточной функции.
Если первая часть дифференциального уравнения имеет производные от входного воздействия, т.е. числитель передаточной функции определяется некоторым многочленом:
|
|
(6) |
то УКП форма имеет вид:
|
|
(7) |
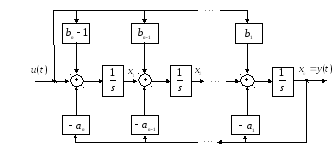
Каноническое
представление удобно для моделирования,
так как матрицы
![]() и
и
![]() имеют минимальное число ненулевых
элементов (рис.1).
имеют минимальное число ненулевых
элементов (рис.1).
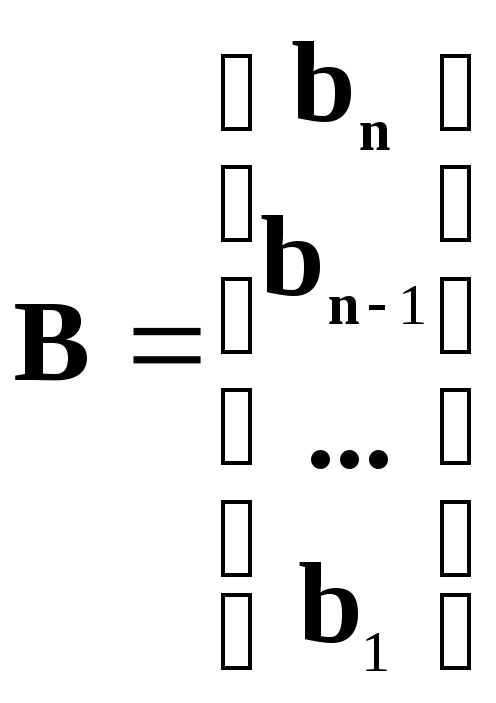
Идентификационное каноническое представление тех же матриц записывается как:
|
|
(8) |
Структурная схема моделирования в форме идентификационного канонического представления (ИКП) приведена на рис.2 [1].
|
|
|
Рис.1. Структурная схема системы в УКП форме |
Сравнение матриц
![]() ,
,
![]() ,
,
![]() ,
записанных в базисах УКП и ИКП, показывает
пути преобразования матриц. Так, если
уравнения записаны в форме УКП (матрицы
имеют подстрочный символ У),
а следует перейти к форме ИКП (матрицы
имеют подстрочный символ И),
то необходимо:
,
записанных в базисах УКП и ИКП, показывает
пути преобразования матриц. Так, если
уравнения записаны в форме УКП (матрицы
имеют подстрочный символ У),
а следует перейти к форме ИКП (матрицы
имеют подстрочный символ И),
то необходимо:
- чтобы
получить
![]() надо транспонировать
надо транспонировать
![]() ,
т.е.
,
т.е.
![]() ;
;
- чтобы
получить
![]() надо транспонировать
надо транспонировать
![]() ,
т.е.
,
т.е.
![]() ;
;
- чтобы
получить
![]() надо транспонировать
надо транспонировать
![]() ,
т.е.
,
т.е.
![]() .
.
|
|
|
Рис.2. Структурная схема системы в ИКП форме |
Переход от базиса УКП к базису ИКП относится к широко используемому, но частному случаю.
В общем случае
необходимо уметь любую матрицу и любой
вектор записывать в разных базисах.
Переход к новому базису осуществляется
с помощью матрицы перехода
![]() ,
которая, согласно теореме, единственна
и вычисляется по формуле:
,
которая, согласно теореме, единственна
и вычисляется по формуле:
|
|
(9) |
где ![]() - пара матриц, заданных в исходном базисе;
- пара матриц, заданных в исходном базисе;
![]() - пара матриц,
заданных в новом (преобразованном)
базисе.
- пара матриц,
заданных в новом (преобразованном)
базисе.
Применим эту
теорему для определения матрицы перехода
![]() от базиса, определяющего матрицы
от базиса, определяющего матрицы
![]() ,
,
![]() ,
,
![]() в форме УКП (обозначим эти матрицы через
в форме УКП (обозначим эти матрицы через
![]() ),
к базису, определяющему эти матрицы в
форме ИКП (обозначим матрицы через
),
к базису, определяющему эти матрицы в
форме ИКП (обозначим матрицы через
![]() ).
).
|
|
(10) |
Так как
![]() ,
а
,
а
![]() ,
то матрица перехода от базиса УКП к
базису ИКП принимает вид:
,
то матрица перехода от базиса УКП к
базису ИКП принимает вид:
|
|
(11) |
Таким образом, можно либо непосредственно из матриц в форме УКП перейти к матрицам в форме ИКП, согласно описанному выше правилу, либо воспользоваться матрицей перехода (11).
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. По заданному дифференциальному уравнению записать передаточную функцию системы и проверить значение на выходе при подаче единичного постоянного внешнего воздействия с помощью соответствующей модели в Simulink.
2. На основании выражений (7) записать матрицы А, В, С в форме управляемого канонического представления (УКП), построить структурную схему согласно рис.1 и модель в Simulink. Сравнить результаты с п.1.
3. Перейти к идентификационному каноническому представлению с помощью правила перехода, сравнить полученные матрицы с выражением (8). Построить структурную схему согласно рис.2 и модель в Simulink. Сравнить результаты с п.1,2.
4. Получить матрицу перехода Р от УКП к ИКП. Записать с ее помощью матрицы в форме ИКП, сравнить с матрицами, полученными при выполнении п.3.
5. Осуществить переход к новому базису с использованием произвольной невырожденной матрицы Р, построить структурную схему и модель в Simulink. Сравнить результат и сделать выводы.
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ
Пусть дано дифференциальное уравнение вида:
|
|
(12) |
1. Запишем передаточную функцию системы
|
|
(13) |
Согласно (6), передаточная функция имеет коэффициенты:
|
|
(14) |
Т.е .
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
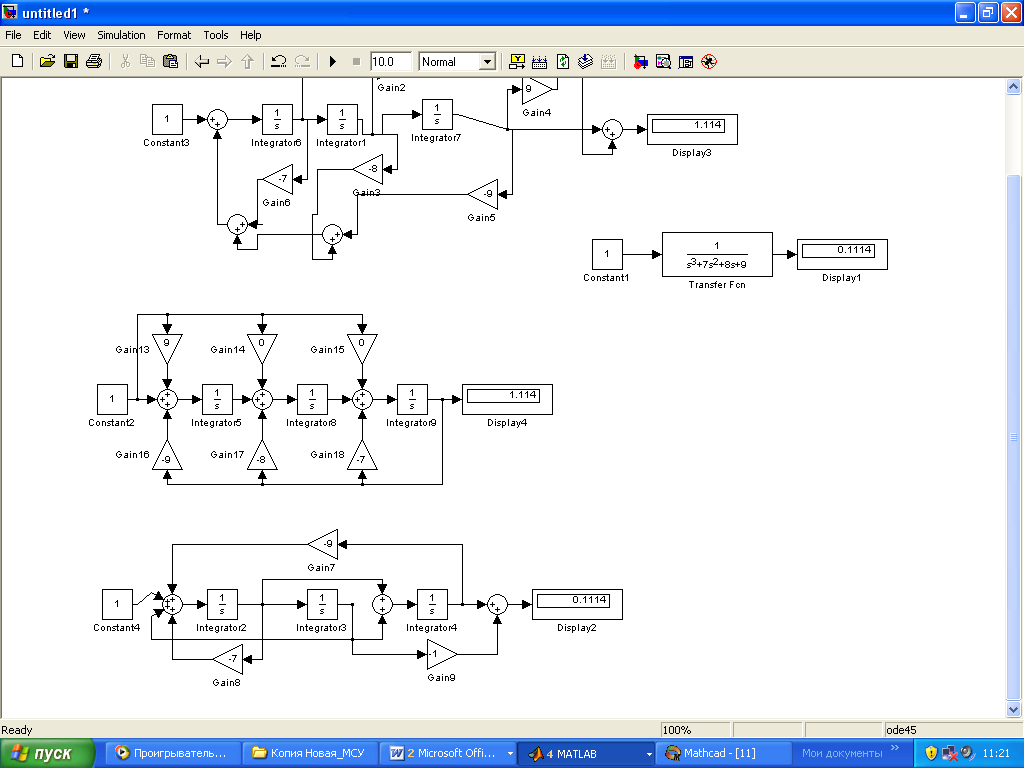
Модель системы в Simulink представлена на рис.3.
|
|
|
Рис.3. Модель системы на основании передаточной функции (13) |
2. Введем обозначения:
|
|
(15) |
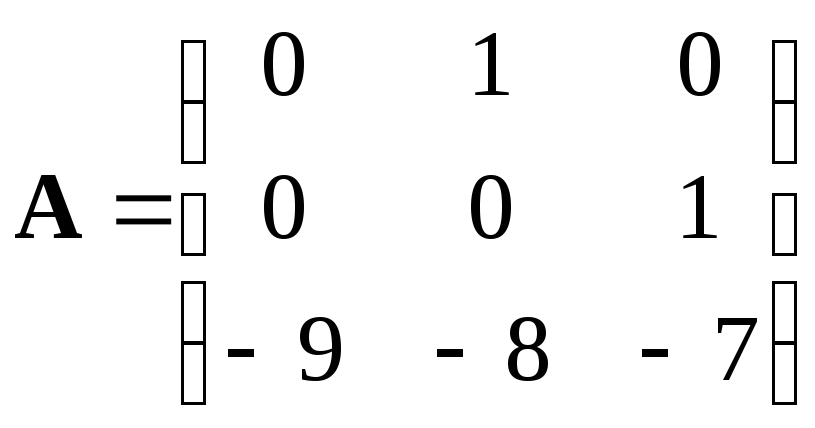
В соответствии с уравнением состояния (15), запишем матрицы:
|
|
(16)
|
С другой стороны, в соответствии с выражением (7), матрицы в форме УКП в общем виде и с учетом численных значений коэффициентов диффе-ренциального уравнения:
|
|
(17)
|
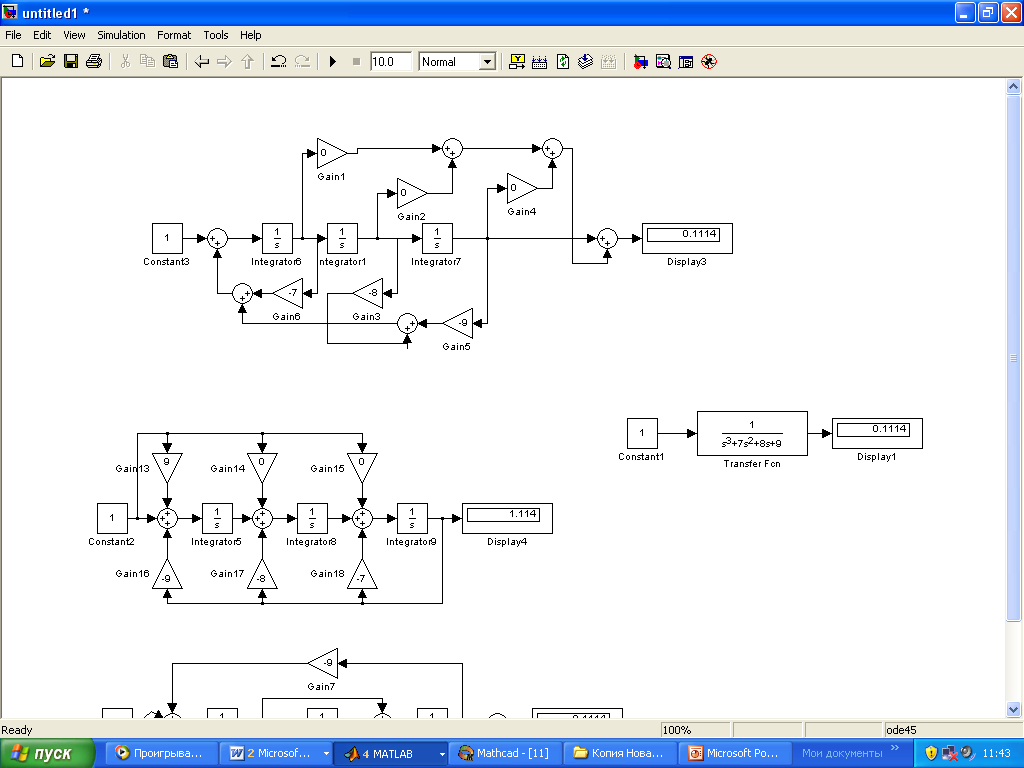
Получаем те же матрицы, что и в (16), т.е. матрицы (16) представлены в форме УКП. Структурная схема, соответствующая этим матрицам, приведена на рис.4, а модель в Simulink - на рис.5.
|
|
|
Рис.4. Структурная схема системы в УКП форме |
|
|
|
Рис.5. Модель системы в УКП форме в Simulink |
Результат на основании моделей рис.3 и рис.5 совпадает, что говорит о том, что обе структуры дают одинаковые внешние данные.
3. Перейдем к идентификационному каноническому представлению с помощью правила:
|
|
(18) |
Тогда имеем:
|
|
(19)
|
С другой стороны, в соответствии с выражением (8) и с учетом численных значений коэффициентов матрицы в форме ИКП:
|
|
(20)
|
Получаем те же матрицы, что и в (19).
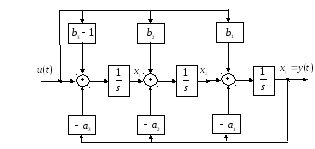
Структурная схема системы в форме идентификационного канонического представления (ИКП) представлена рис.6, а компьютерная модель в Simulink - на рис.7.
|
|
|
Рис.6. Структурная схема системы в ИКП форме |
Результаты пунктов 1, 2 и 3 идентичны, т.е. изменяя внутреннюю структуру системы, получили одинаковые внешние параметры.
|
|
|
Рис.7. Модель системы в ИКП форме в Simulink |
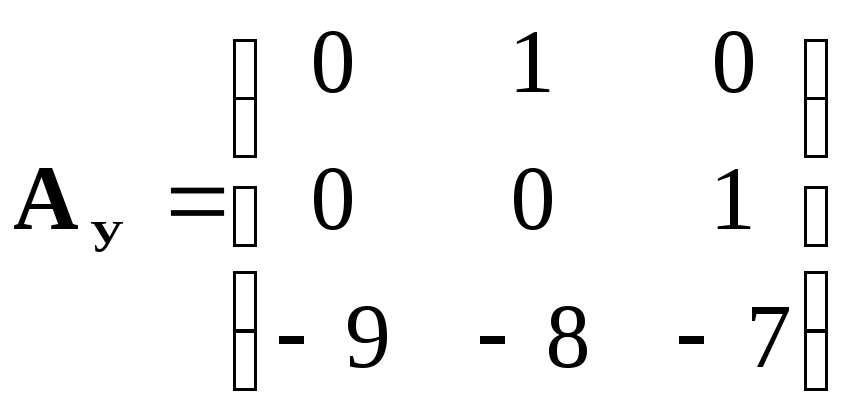
4. Получим матрицу перехода Р от УКП к ИКП с помощью выражения (11). Отдельные матрицы и матричные произведения этого выражения имеют вид:
|
|
|
|
Для вычисления обратной матрицы воспользуемся формулой:
|
где
Мi,j – миноры матрицы А. |
|
|
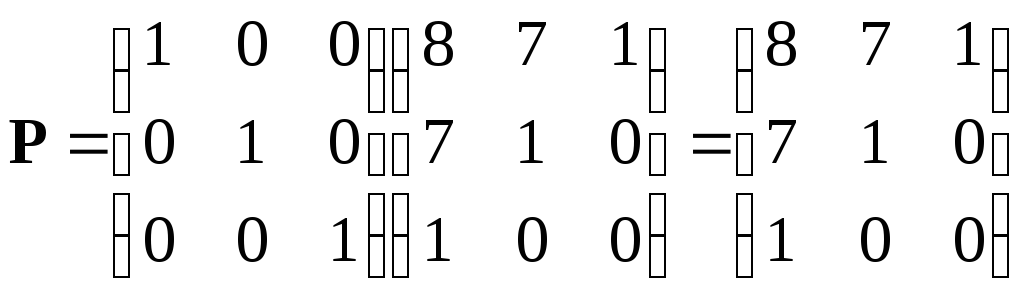
Тогда матрица перехода:
|
|
(21) |
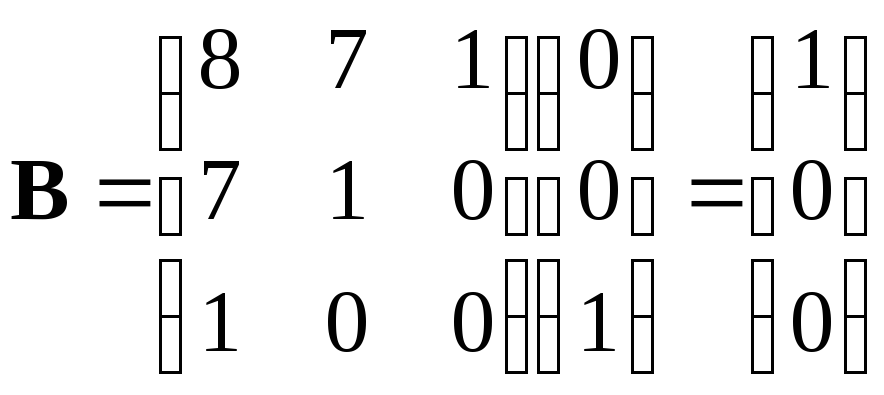
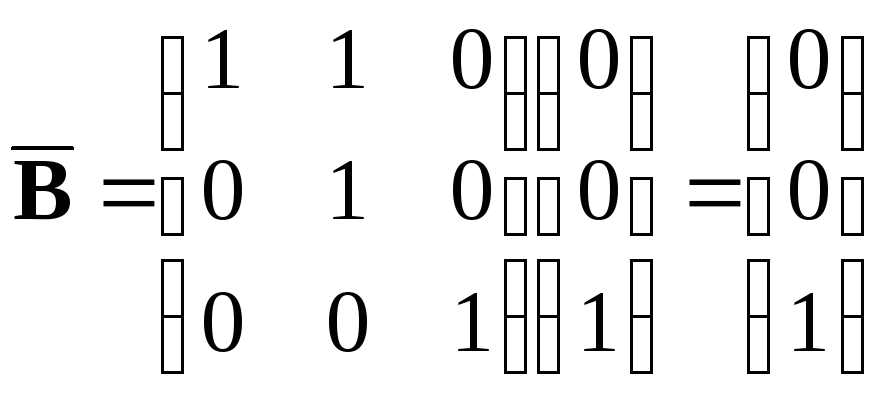
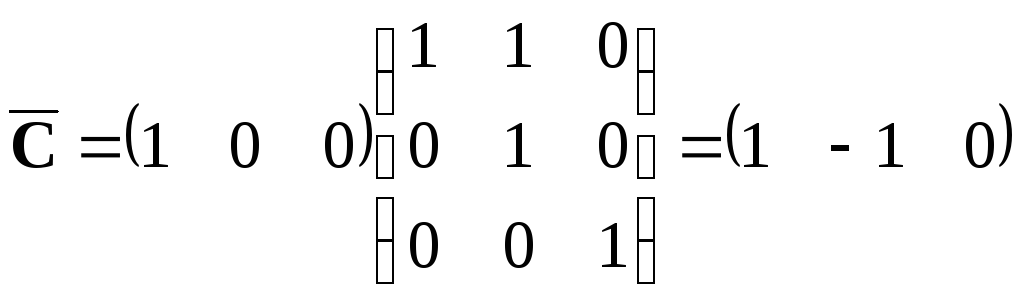
Запишем матрицы в форме ИКП на основании выражений:
|
|
(22) |
В результате имеем:
|
|
|
|
|
|
|
|
|
Результаты получены идентичные результатам пункта 3, что говорит о верности расчета матрицы перехода.
5. Осуществим переход к новому базису с использованием произвольной невырожденной матрицы Р, которую примем в виде:
|
|
(23) |
Определитель данной матрицы равен 1, т.е. не нулевой, следовательно, данная матрица является невырожденной. На основании выражений (22) матрицы в новом базисе имеют вид:
|
|
(24)
|
Дифференциальные уравнения, соответствующие новому базису:
|
|
(25) |
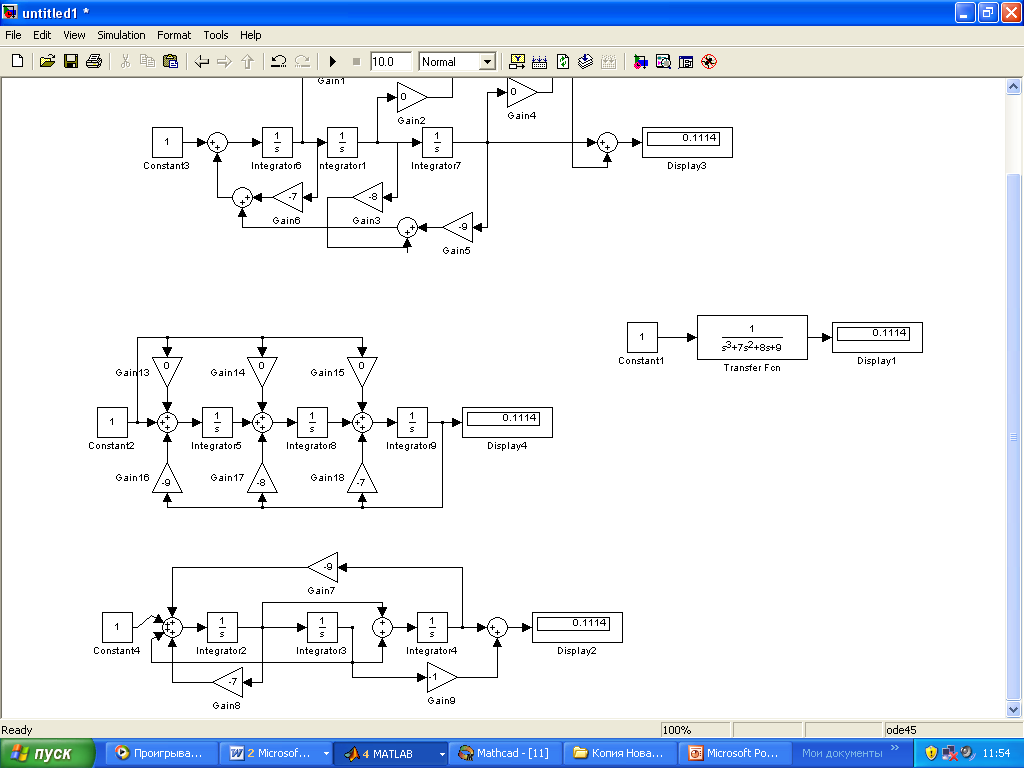
Модель в Simulink на основе системы уравнений (25) представлена на рис.8. Результаты и в этом случае совпадают.
|
|
|
Рис.8. Модель системы на основании уравнений (23) |
ВАРИАНТЫ ЗАДАНИЙ
|
№ п/п |
Передаточная функция исследуемой системы |
№ п/п |
Передаточная функция исследуемой системы |
|
1 |
2 |
3 |
4 |
|
1 |
|
13 |
|
|
2 |
|
14 |
|
|
3 |
|
15 |
|
|
4 |
|
16 |
|
|
5 |
|
17 |
|
|
6 |
|
18 |
|
|
7 |
|
19 |
|
|
8 |
|
20 |
|
|
9 |
|
21 |
|
|
10 |
|
22 |
|
|
11 |
|
23 |
|
|
12 |
|
24 |
|
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Что в системе изменяется, а что нет при использовании преобразований подобий?
2. Какое количество
матриц
![]() ,
,
![]() и
и
![]() можно записать для одной конкретной
системы?
можно записать для одной конкретной
системы?
3. Как по
дифференциальному уравнению записать
матрицы
![]() ,
,
![]() и
и
![]() в управляемом и идентификационном
каноническом представлениях?
в управляемом и идентификационном
каноническом представлениях?
4. Как записать
матрицы
![]() ,
,
![]() и
и
![]() в форме ИКП, если известны эти матрицы
в управляемой канонической форме?
в форме ИКП, если известны эти матрицы
в управляемой канонической форме?
5. Как рассчитывается матрица перехода от базиса УКП к базису ИКП?
6. Какой вид имеет структурная схема системы, заданной в форме УКП?
7. Какой вид имеет структурная схема системы, заданной в форме ИКП?
ВРЕМЯ, ОТВЕДЕННОЕ НА ВЫПОЛНЕНИЕ РАБОТЫ
1. Подготовка к работе – 1,0 акад.час
2. Выполнение работы – 3,0 акад.часа
3. Оформление работы – 1,0 акад.час
ЛИТЕРАТУРА
1. Соседка В.Л. Современная теория управления: учеб.пособие для студ. высш.учеб.заведений / В.Л.Соседка. – Днепропетровск: НГУ, 2003. – 144 с.
2. Филипс Ч. Системы управления с обратной связью / Ч.Филлипс, Р.Харбор. – М.: Лаборатория базовых знаний, 2001. – 616с.
3. Матричные методы расчета и проектирования сложных систем автоматического управления для инженеров / под ред. К.А.Пупкова и Н.Д.Егупова. – М.: Изд-во МГТУ им.Баумана, 2007. – 664 с.

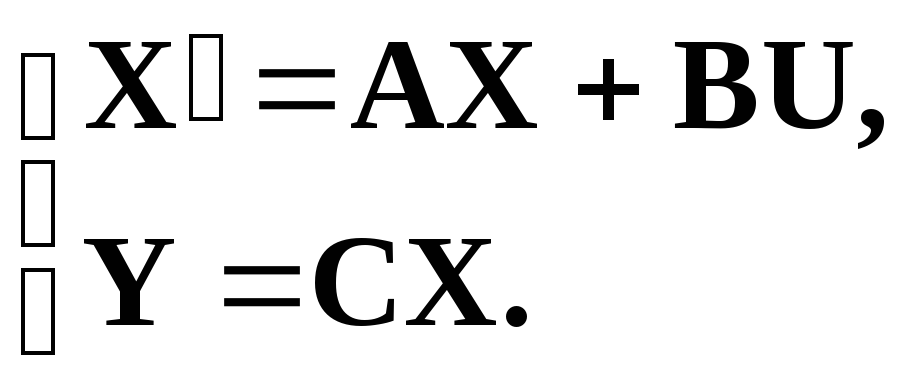 .
.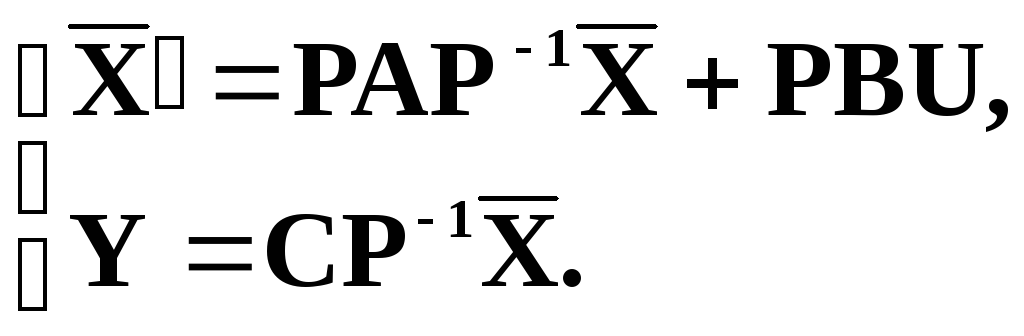
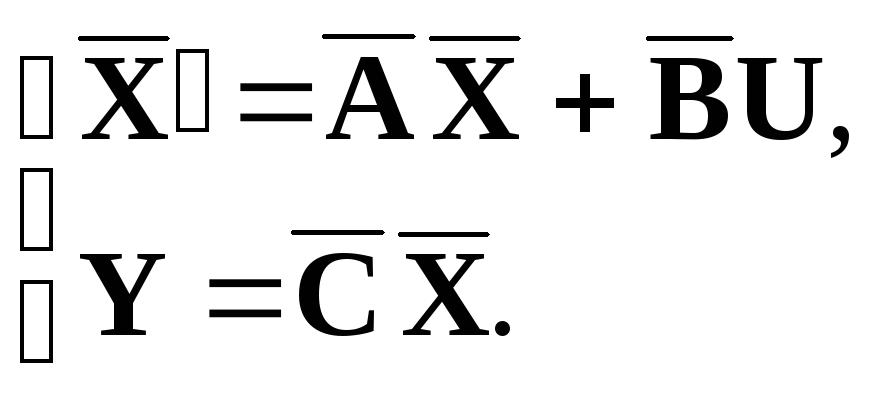
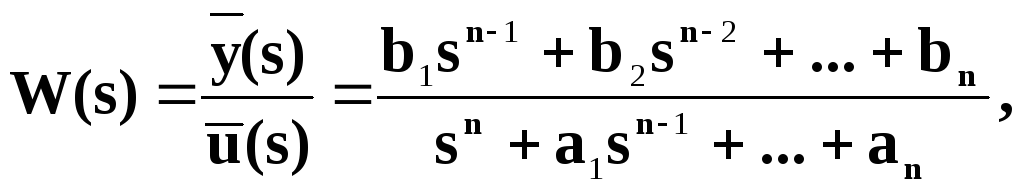
 ,
,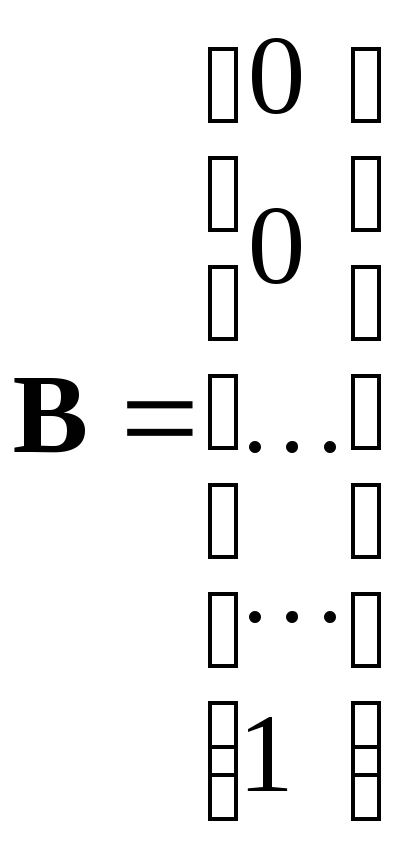 ,
,  ,
,  ,
, 
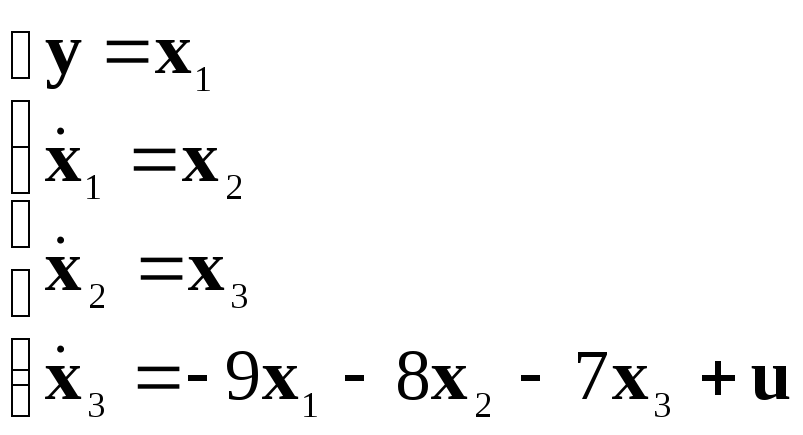 .
. ,
,
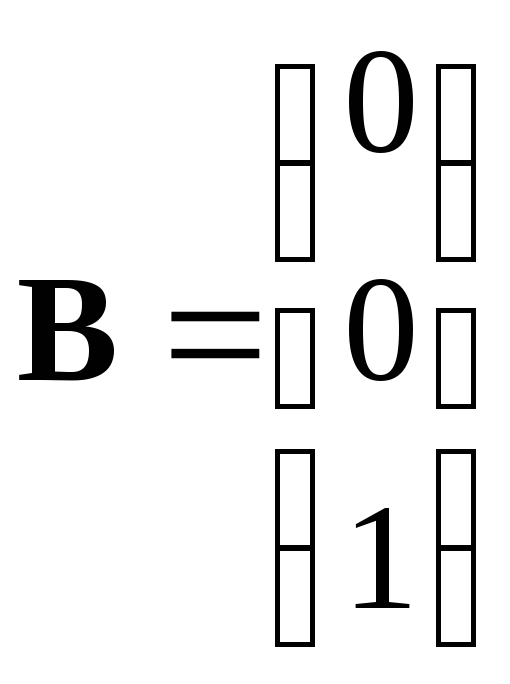 ,
,
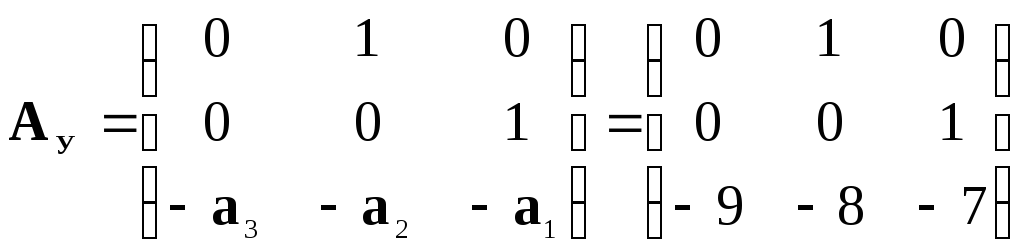 ,
,
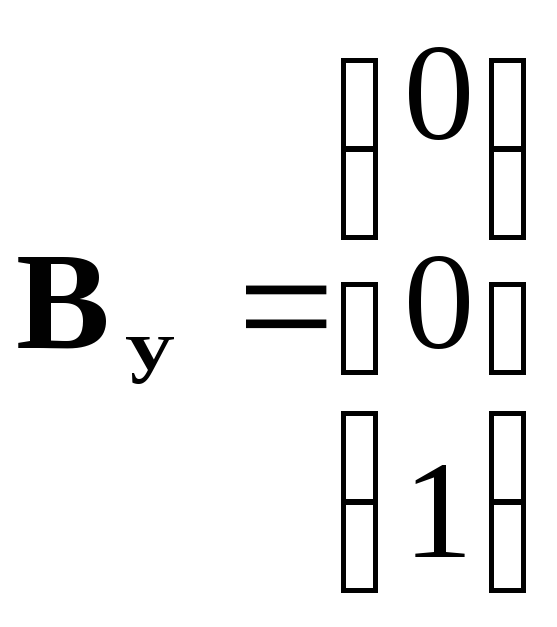 ,
,

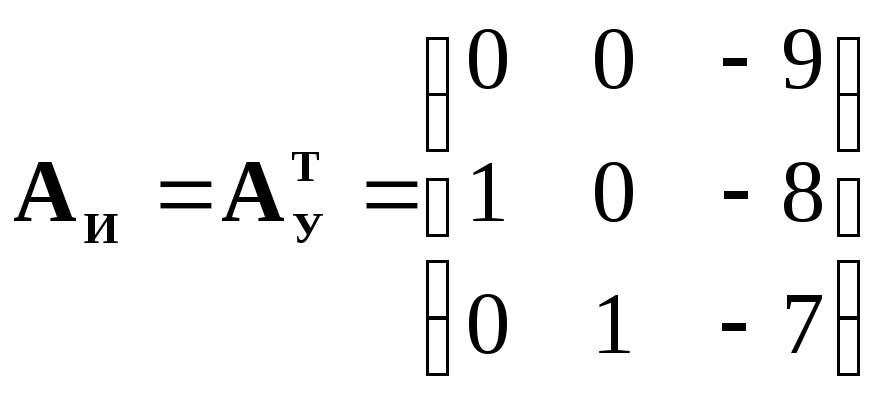 ,
,
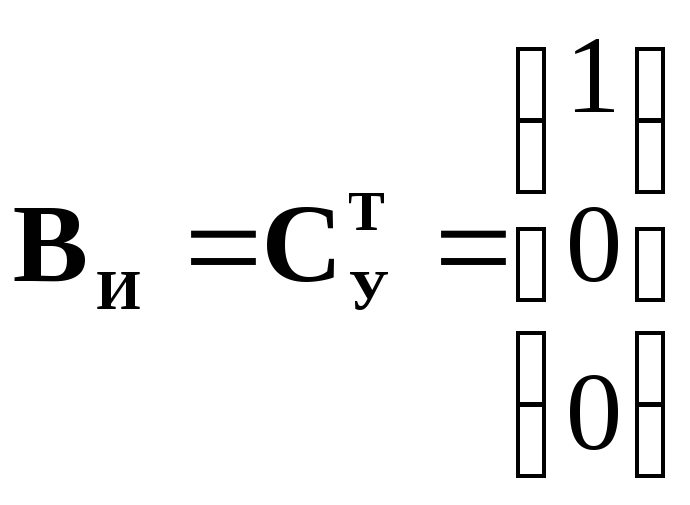 ,
,
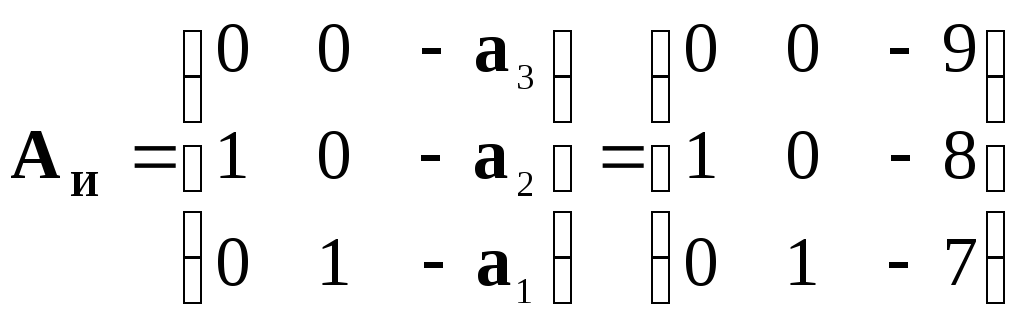 ,
,
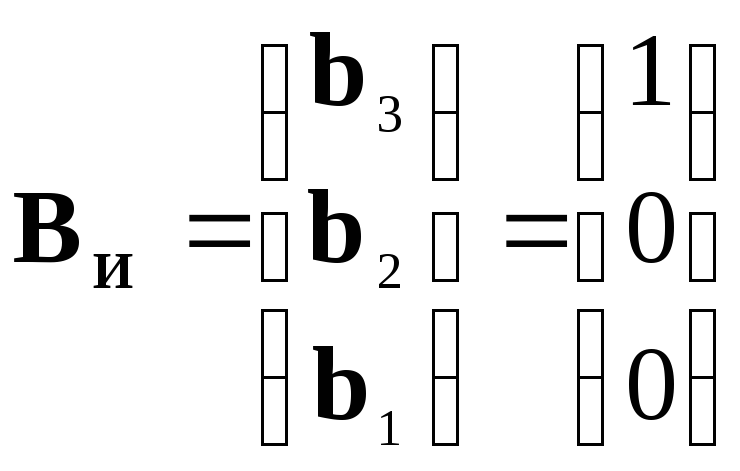 ,
,
 ,
,
 ,
,

 ,
,
 ,
,
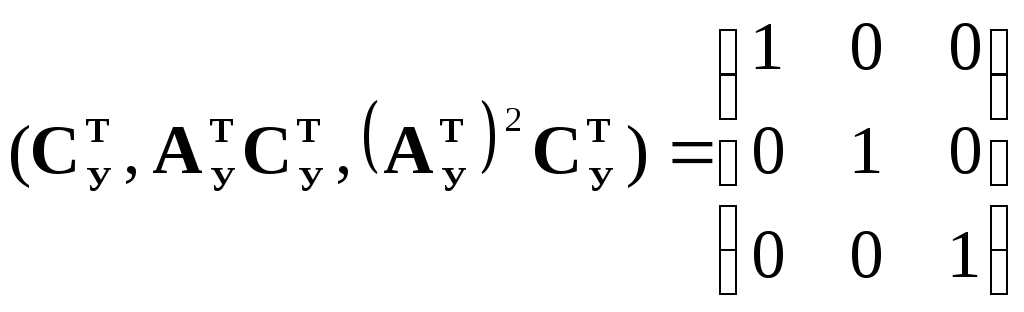 ,
,
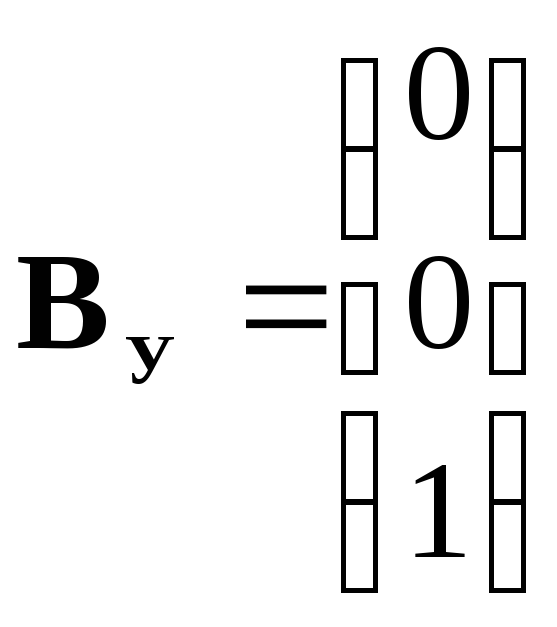 ,
,
 ,
,
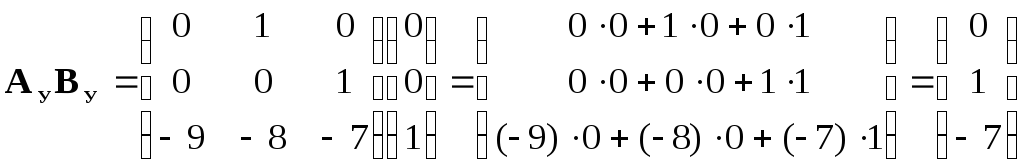 ,
,
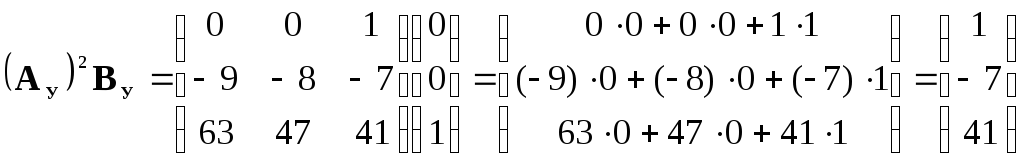 ,
,
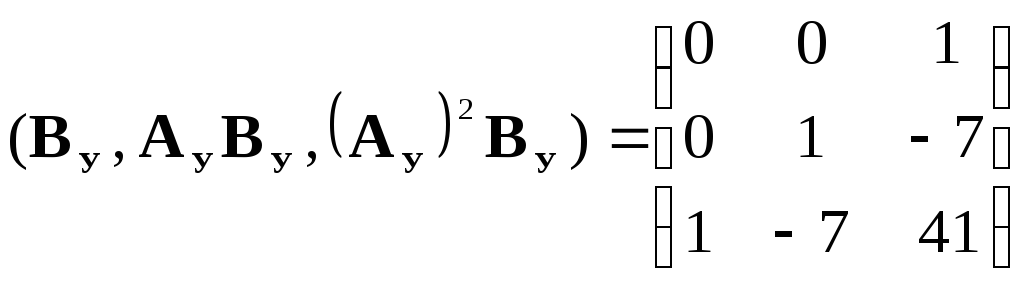 .
.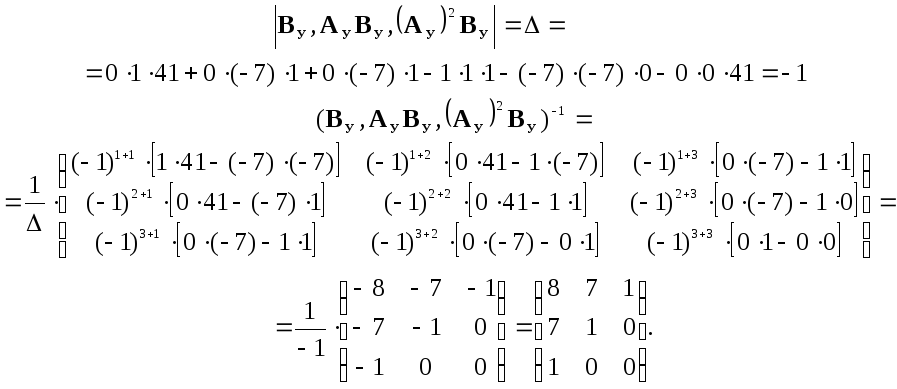
 .
.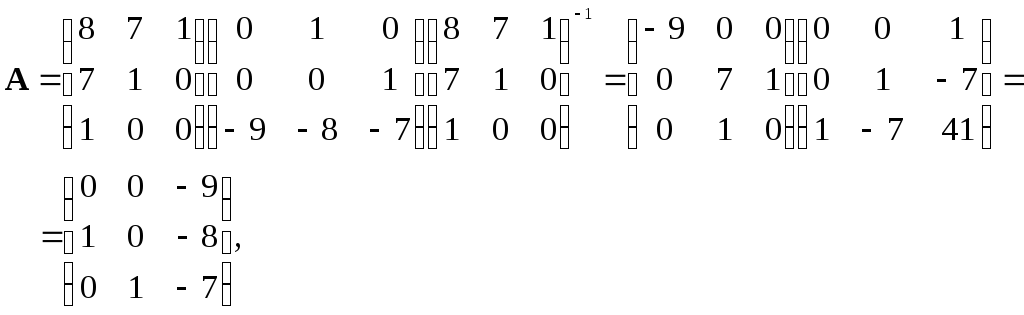 .
.
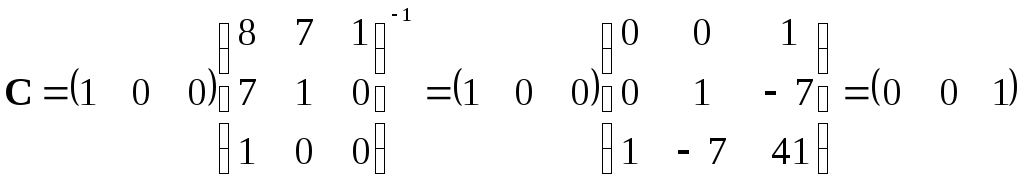
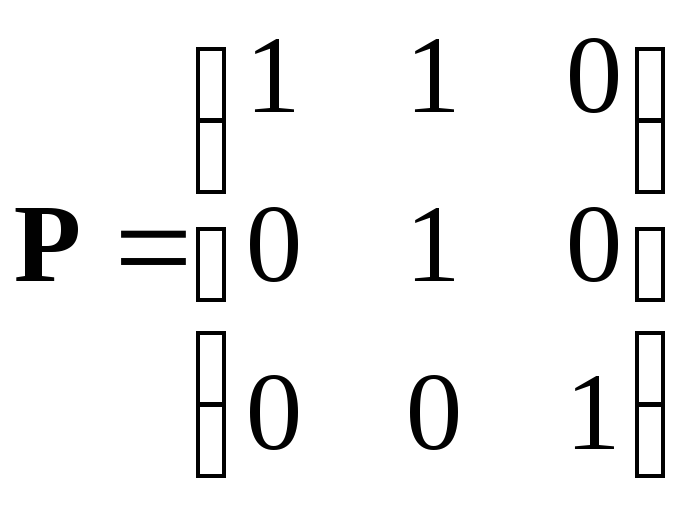 .
. ,
,
 ,
,
 .
.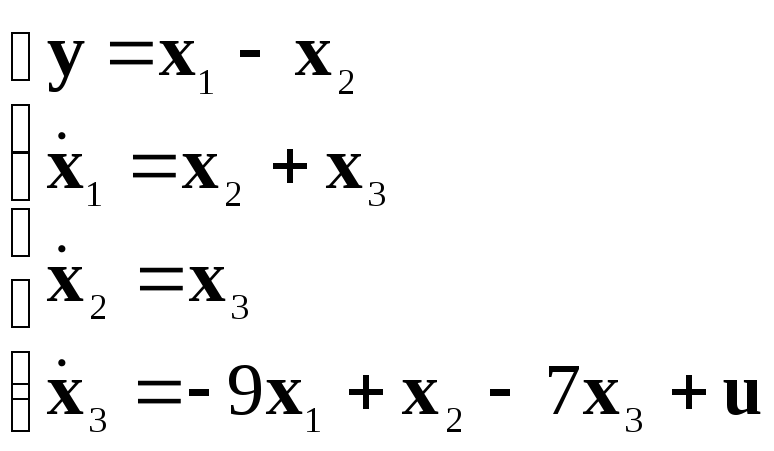 .
.