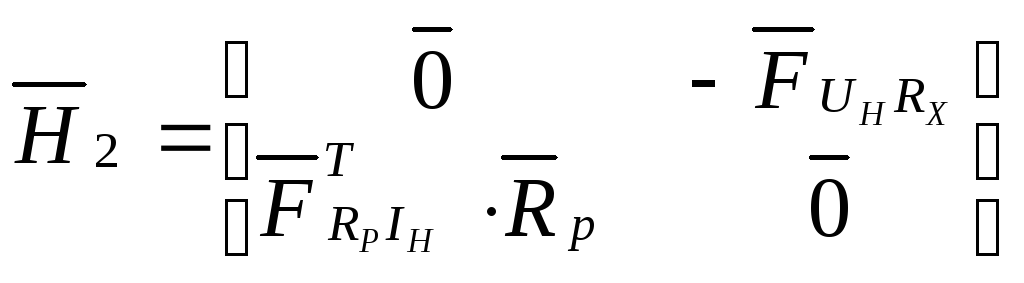2. Матричные коэффициенты уравнения состояния.

По матрице главных сечений для произвольной схемы

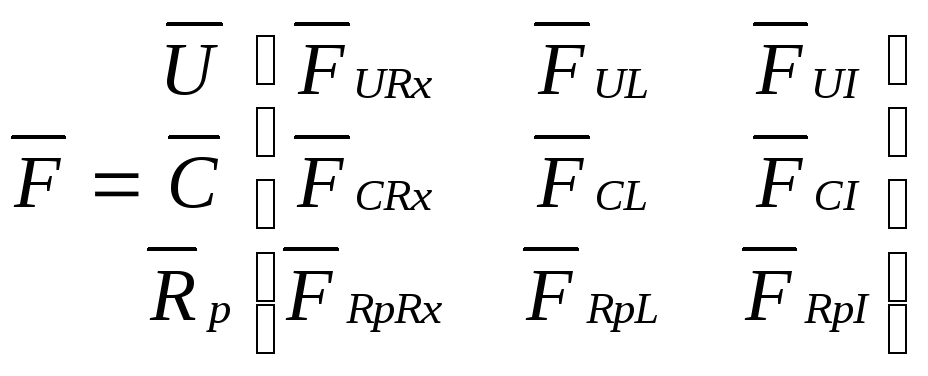
запишем топологические уравнения для и .

(10)

(11)

Компонентные уравнения для индуктивных и емкостных элементов имеют вид:

; (12)

Запишем в (10) и (11) левые части равенств выражениями (12)

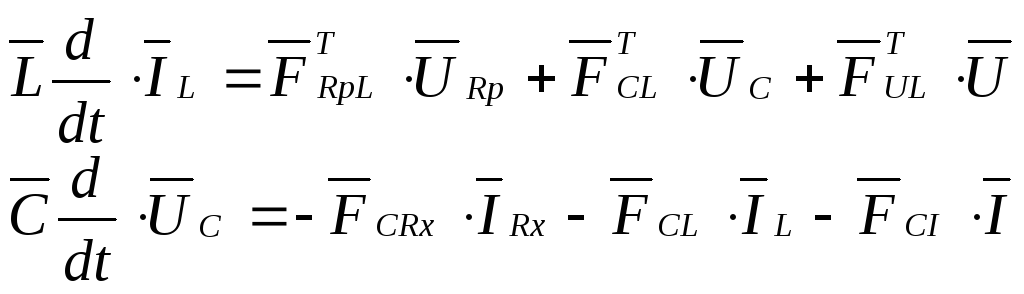(13)

Далее выразим через , используя (4)

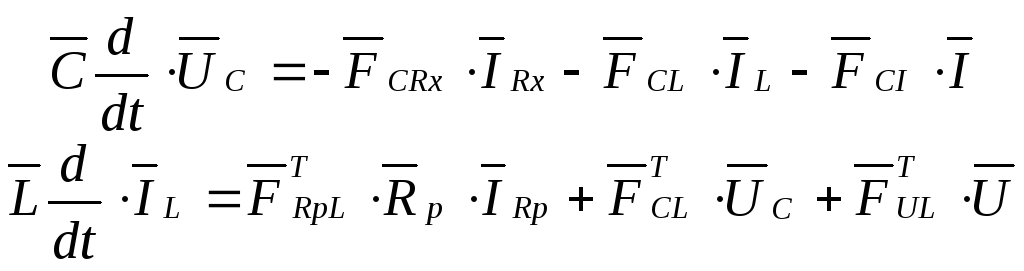(14)

Объединим оба уравнения в одно матричное. Получим:

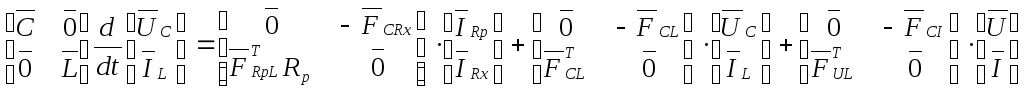
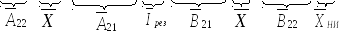(15)

Здесь и - матрицы емкостей и индуктивности

;

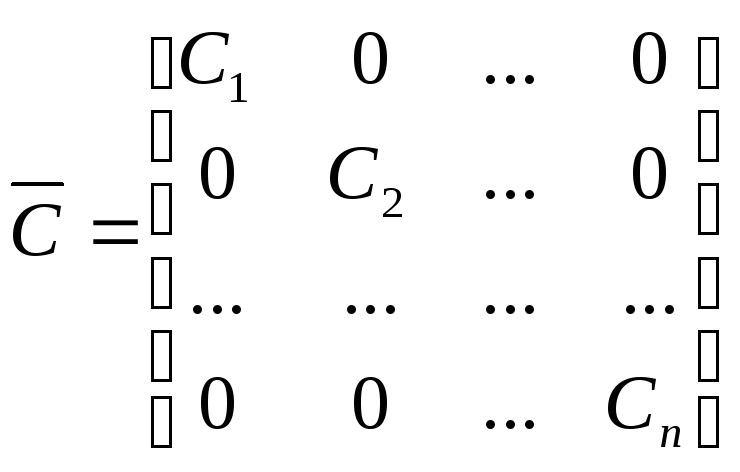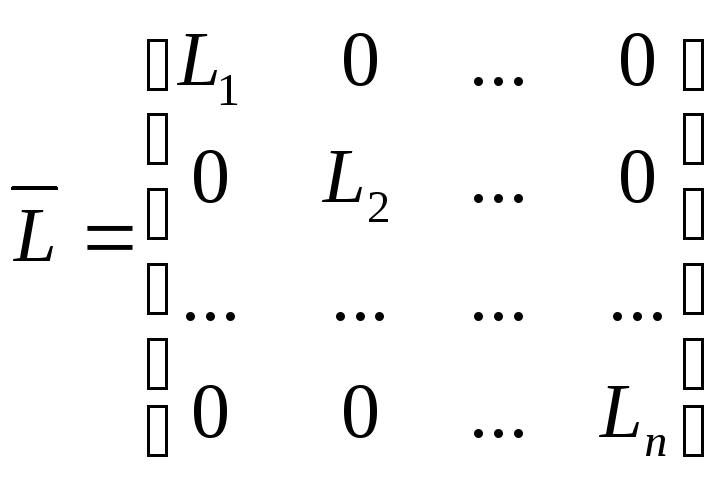
Отсюда

(16)

Раньше было выведено:

Подставим его в матричное уравнение. Получим

(17)

или

(18)

3. Матричные коэффициенты уравнения выхода.

Отклик Х_вых на выходе схемы может стать, как уже отмечалось, напряжением U_вых или током і_вых. Если Х_вых= U_вых, то его можно представить электрической суммой напряжений ветвей при обходе некоторого контура от одной (начальной) выходной клеммы схемы ко второй (конечной) клемме.

Если Х_вых= і_вых, то он может быть определен алгебраическим суммированием токов ветвей, подходящих к выходной цепи.

3. Матричные коэффициенты уравнений математической модели цепи с нелинейными резистивными элементами.

Рассмотрим алгоритм расчета матричных коэффициентов, входящих в уравнения математической модели цепи с нелинейными резисторами.

Как и для линейной схемы, эти коэффициенты должны выражаться через подматрицы матрицы главных сечений .

Особенность матрицы главных сечений для цепи с нелинейными резистивными элементами в том, что под и понимают линейные резистивные ребра и хорды, а нелинейные резисторы образуют строки и столбцы .

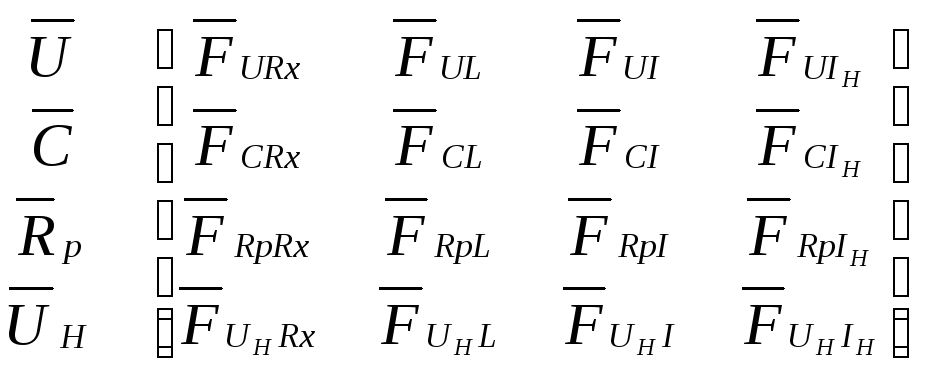
Для вывода выражений, определяющих матричные коэффициенты уравнения токов линейных резистивных элементов и уравнения состояния цепи с нелинейными резистивными элементами, требуются выкладки, аналогичные тем, которые проводились при выводе выражений коэффициентов аналогичных уравнений линейной цепи.

После таких выкладок получим

(19)

или

(20)

где

;

; (21)

.

(22)

или

(23)

где

;

; (24)

.

Коэффициенты , , , имеют тот же смысл и определяются теми же выражениями, что и аналогичные коэффициенты уравнений линейной цепи.

Приведем лишь величины, входящие в выражение коэффициентов и .

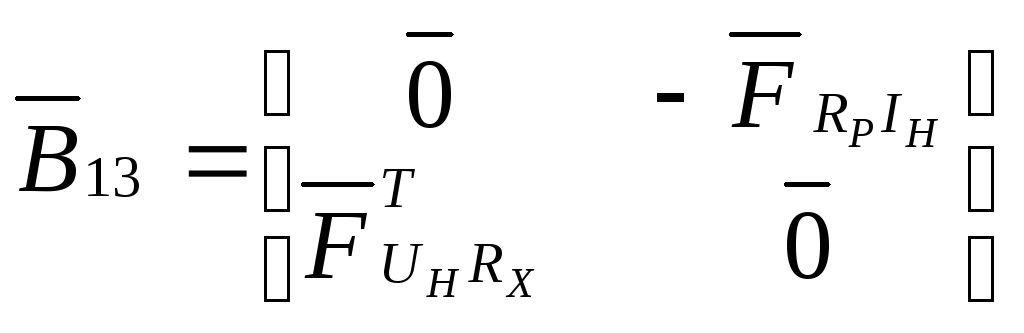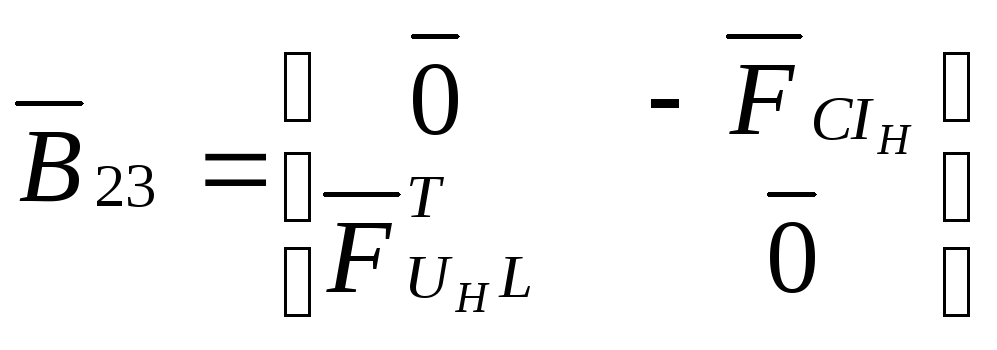; (25)

Найдем коэффициенты в уравнении

(26)

Можно показать, что

;

;

.

При этом:

(28)

; ;

;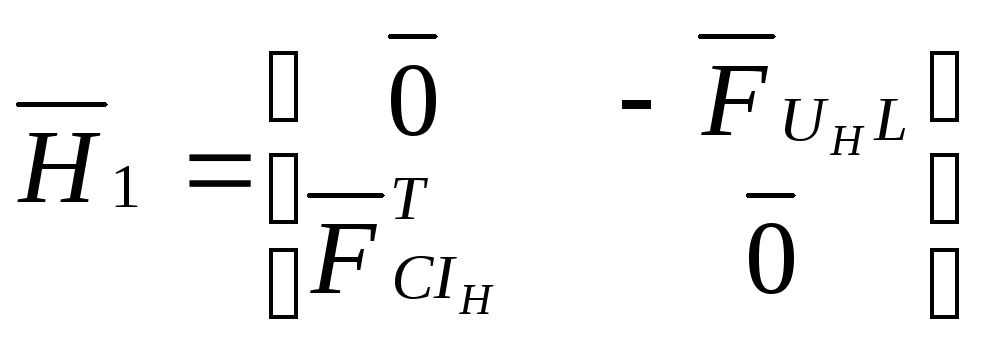
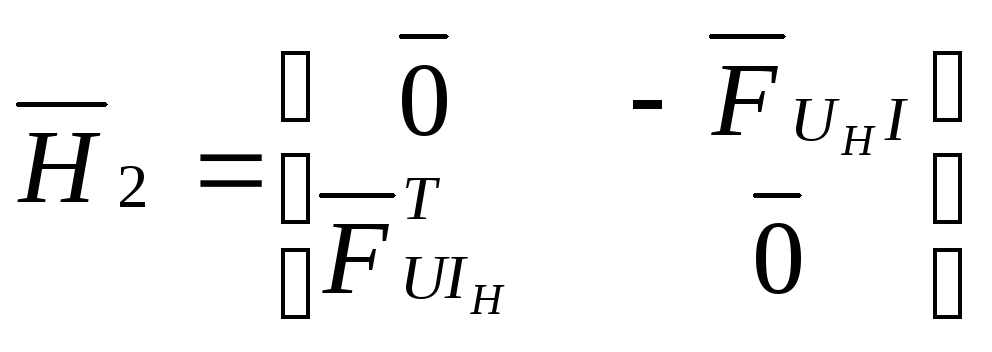
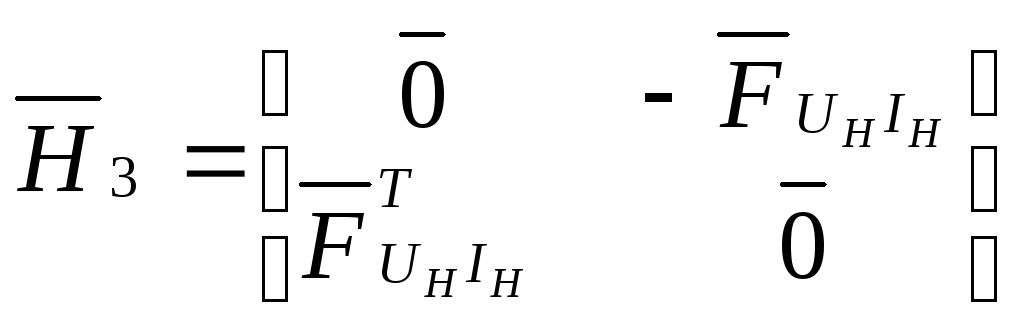