Сетевые модели (n-схемы)
В практике моделирования часто приходится иметь дело со сложными системами, где одновременно параллельно протекает несколько процессов.
Самым распространенным подходом для моделирования таких систем являются сети Петре.
Формально сети Петре задаются вида:
,
где В– конечное множество символов, называемых позициями;
D– конечное множество символов, называемых переходами;
I– входная функция;
О– выходная функция.
Входная функция Iотражает переходdjв множество выходных позицийdi:
.
Выходная функция О отражает переход djв множество выходных позицийdi:
.
Графически N-схема (PetriNets) изображаются в виде двудольного ориентированного мультиграфа представляющего собой совокупность позиций и переходов.
Таким образом, мы изобразили N-схему, которая изображается подмножеством:
,
- позиции,
- переходы,
,
,
,
,
,
,
,
.
Приведенное представление N-схемы может использоваться только для отражения в статике моделируемой системы.
Для отображения динамики вводится функции маркировки (разметки), а также может использоваться временные сети, Е-сети, сети Мерлина и т.д.
Комбинирование модели А-схемы
Для описания обобщенных систем (непрерывных и дискретных, детерминированных и стохастических) используется понятие агрегативной системы, представляющей собой формальную схему общего вида, называемая А-схемой (Aggregatesystem).
При агрегативном описании сложный объект разбивается на конечное число подсистем, сохраняя при этом связи, обеспечивающие их взаимодействие, т.е. в качестве элемента А-схемы выступает агрегат, а связь между агрегатами внутри системы S и с внешней средой Е осуществляется с помощью оператора сопряжения.
Агрегат, если может рассматриваться как А-схема, т.е. разбиваться на элементы (агрегат следующего уровня).
Агрегат описывается следующим множеством
и множеством случайных операторов
.
Где Т– множество моментов времени,
Х– множество входных сигналов,
Y– множество выходных сигналов,
Z– множество состояний,
Н– множество внутренних параметров системы,
V– описывает процесс функционирования агрегата в случае воздействия входного сигнала,
U– описывает состояние агрегаты, если интервал времени не содержит не одного момента поступления сигналов,
W– описывает скачки состояния в особые моменты времени не являющиеся моментами поступления входных сигналов,
Z(Y)– подмножество в множестве состояний Z, который является моментом выдачи выходного сигнала, определяемая оператором выходаG.
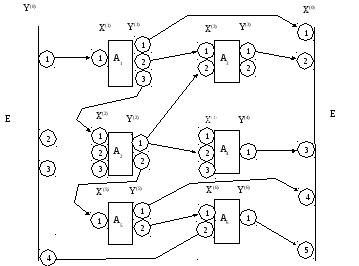
Функционирование, рассмотренное А-схемой связано с переработкой информации, передача, которой показана стрелками. Вся информация, циркулирующая в схеме делится на внутреннюю и внешнюю. Внешняя информация проступает от внешних объектов не являющаяся элементами А-схемы. А внутренняя информация вырабатывается агрегатами самой А-схемы. Обмен информации между элементами А-схемы и внешней средой, называется полюсами А-схемы, при этом при этом различают входные полюса агрегата и выходные полюса.
Агрегаты не являющиеся полюсами, называются внутренними.