Параллельное соединение распределения блоков

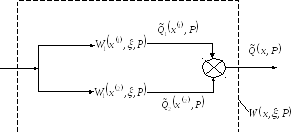
Пусть нам известны передаточные функции идвух распределенных блоков ((27)и (28)), выходные сигналы которыхиопределены на пространственных областяхипри параллельном соединении этих блоков с общим входом, их выходные сигналы складываются в каждой точке- пространственной области, на которой определена соответствующая сумма, рассматривающая в качестве выхода этого соединения и следовательно:

Если , то и, откуда

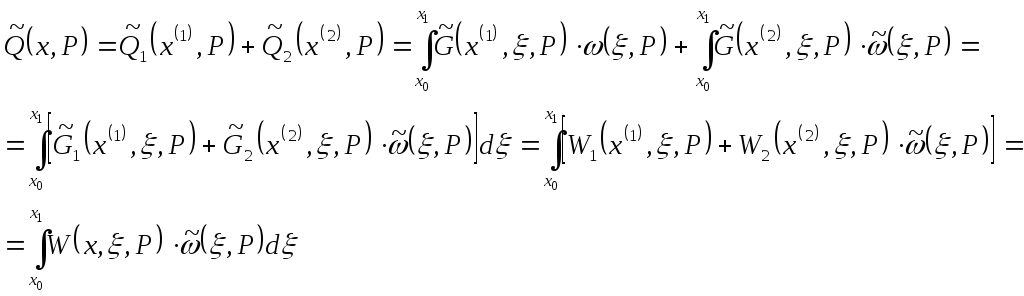(30)

где и

То есть передаточная функция параллельного блока:

где

(31)

Данный вывод распространяется на любое число параллельных блоков.

Последовательное соединение распределенных блоков

При последовательном соединении двух блоков с передаточными функциями ив силу уравнения (27), получаем соотношение, связывающего вход и выход каждого из них.

(32)

Здесь - выход второго блока выход всего соединения,- выход сигнала первого блока, который одновременно является входным сигналом- второго блока.

- пространственная переменная внешнего воздействия,

- пространственная переменная второго блока.

Последовательное соединение имеет смысл при , что называется условием согласования.

Пространственную область определения выходного сигнала предыдущего блока и сигнала последовательного совпадают.

Таким образом, передаточная функция последовательного блока, это есть интеграл по последовательной координате.

(33)

Передаточная функция последовательного соединения определяется в форме пространственной композиции (33) передаточных функций отдельных блоков, связанных в порядке обратном по отношению к порядку их следования в схеме данного соединения.

Поэтому менять сомножители нельзя, так как интеграл может изменить свои значения.

Поэтому последовательное соединение называется некоммутативным.

Полученные выводы распространяются на любое число последовательных блоков

Типовые распределенные блоки

Типовой объект управления с распределенными параметрами с входным воздействием и выходом, может аналогично объектами с распределенными параметрами рассматриваться в виде распределенного блока (черного ящика).

Отличие заключается в том, что входная и выходная величины, зависящие не только от времени, но и от пространственных аргументов.

В общем случае объект с распределенными параметрами можно представить:

СРП:

ССП:

Переходный х-блок

Представляет собой распределенный блок с сосредоточенным входным сигналом и распределенным выходным.

Это один из наиболее распространенных на практике вариантов для которого стандартизирующая функция.

То есть рассматривается объект с сосредоточенным внешним воздействием и фиксированным закономпространственного распределения входного сигнала.

Тогда в соотношении, связывающим вход объекта с управлением вынесем управляющее воздействие за знак пространственного интеграла:

,

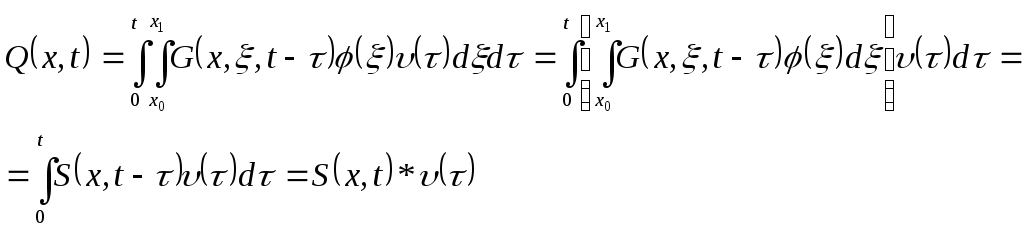где * - операция свертки,

,

- пространственная композиция.

Если представить в виде произведенияи, где- удельная величина источников тепла, выделяемого в нагретом теле,- закон ее распределения по пространственной координате х-блок первоготипа.

переходной -блокпредставляет собой блок с распределенным входным сигналом и сосредоточенным выходным.

В качестве последнего рассматривается значение функции состояния в одной ихилификсированных точках, где.

Подобная ситуация может возникнуть, например, при формировании соответствующего сигнала обратной связи.

Переходный -блок– это распределенный блок с сосредоточенными входами и выходами, моделирует поведение функций состояния объектафиксированных точкахдляпри сосредоточенном управлении.

Аналогично характеризуется объект с сосредоточенными параметрами, однако, -блок отличается от ОСП видом своей функции Грина.

Четвертый тип. Пространственное воздействие при фиксированном характереизменение входного сигнала во времени. Такие блоки не имеют аналогов в сосредоточенных системах.

Задача нагрева тела в распределенных параметрах и ее общее решение

Пример:

Рассмотрим процесс нагрева тела:

В простейшем случае рассмотрим тело геометрически правильной формы с одномерным распространением тепла на отрезке от –RдоRс симметрическими условиями на границах. Пренебрегая температурной зависимости мощности внутреннего тепло отделения, рассмотрим неравномерное распределение только по одной из пространственных координат.

Уравнение при нагреве неподвижного тела сводится к следующему уравнению теплопроводности:

.

С начальными условиями ,.

И граничными условиями второго рода:

,,

,,

- коэффициент температуры проводности.

- коэффициент формы тела,

- для бесконечной пластины толщенной,

- бесконечный цилиндр радиусом,

- шар, радиусом,

- удельная теплоемкость,

- коэффициент теплообмена,

- коэффициент теплопроводности.

В качестве выхода объекта выступает нестационарное температурное поле , а в роли внешних воздействий – удельная мощность внутреннего тепловидения, плотность теплового потокана поверхностии начальные распределения температур.

Каждый из этих воздействий может рассматриваться в качестве управления внутреннего или граничного неуправляемого внешнего фактора (возмущения).

Общее решение в соответствии с (21) на указанные входные воздействия при заданном температурном состоянии.

.

Здесь функция Грина во втором двойном интеграле характеризует распределение температуры, возбуждаемый точечным источником тепла вида -функции сосредоточенной в момент временив точке.

Частными случаями функции Грина являются:

1. Функция Грина характеризует распределение температуры возбуждаемая точечным источником тепла вида-функции, сосредоточенной в точкев начальный момент времени.

2. Функция Грина при.

Импульсная передаточная функция (функция Грина) Является решением задачи,

,

,

,

,

при нулевых начальных и однородных граничных условиях.

Здесь используется разложение в бесконечный ряд Фурье по тригонометрической системе функции с зависящим от времени коэффициентами в виде экспоненты с отрицательными показателями степени быстровозрастающими по абсолютной величине.

.