1.Непрерывно-детермин-ные (н-д) модели (d-схемы)

Рассмотрим н-д подход на примере дифференциальных уравнений. Дифференциальными уравнениями называются такие уравнения в которых неизвестными является функция одной или нескольких переменных, причем в уравнения входят не только функции но и их производные.

Общий вид д.у.: y = f(y,t), t – неизвестная величина (время)

Рассмотрим две формализации процесса функционирования двух систем различной физической природы: механической и электрической.

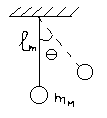
1. Колебания маятника.

При малых отклонениях колебания маятника можно описать уравнением:

m_м l_м² (d²θ/dt²) +m_м l_м g θ(t) = 0

где m_м , l_м – масса и длина маятника, g=9,8

2. Колебательный контур

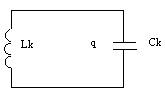
L_к (d²q/dt²) + q(t)/C_к = 0

где L_к – индуктивность катушки, q, C_к – заряд и емкость конденсатора.

Обозначим: 1 2

h₀ = m_м l_м² ; h₀ = L_к

h₁ = 0 ; h₁ = 0

h₂= m_м l_м g ; h₂ = 1/C_к

z(t) = θ(t) ; z(t) = q(t)

Получим: h₀ z”(t) + h₁ z’(t) + h₂ z(t) = 0

Если на систему действует внешнее воздействие x(t), то уравнение будет иметь вид:

h₀ z”(t) + h₁ z’(t) + h₂ z(t) = x(t).

В первом случае x(t) – внешняя сила, приложенная к маятнику, во втором случае x(t) – источник энергии; z(t) – состояние системы (выходная величина).

С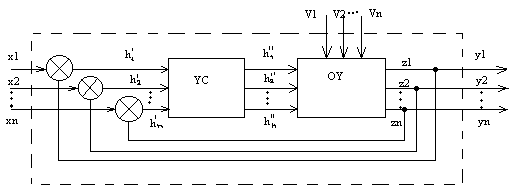помощьюD-схем описывают также САУ. В этом случае реальный объект представляется в виде двух систем: управляющей системы и управляемой.

x(t) – вектор входных воздействий,

h’(t) – сигнал рассогласования,

h”(t) – вектор управляющих воздействий,

V(t) – вектор возмущающих воздействий,

Z(t) – вектор состояния системы,

Y(t) – вектор выходных переменных.

Задачей САУ является изменение выходной величины согласно заданному закону функционирования с зад. точностью. При проектировании и эксплуатации САУ необходимо выбрать такие параметры системы, которые обеспечивали бы зад. точность и устойчивость системы.

2. Дискретно-детерминированные

(д-д) модели (F-схемы).

Д-д модели в своей основе содержат теорию автоматов. На основе этой теории система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свое внутреннее состояние лишь в допустимые момент времени. Автомат можно представить в виде черного ящика, на кот. подаются входные воздействия и снимаются выходные и кот. может иметь множество внутренних состояний.

Автомат, у кот. множество входных переменных и множество внутренних состояний, а следовательно и множество выходных состояний конечно называется конечным автоматом.

Автомат F можно описать множеством входных, выходных, внутренних состояний, начальным значением z₀, функцией переходов φ и функцией выходов ψ: F = < X, Y, Z, z₀, φ, ψ >.

Функция перехода φ определяет состояние z’, в кот. перейдет система если она находилась в состоянии Z и на ее вход поступило входное воздействие X: z' = φ(z, x).

Функция выхода ψ определяет выходное значение Y, кот. принимает система, если она находилась в состоянии Z и на ее вход поступил сигнал X: y = ψ(z, x).

Для задания автомата используется табличный или графический способ. При табличном способе в строках записываются входные воздействия автомата X, а в столбцах – состояния Z.

z₀ z₁ z₂ z₃

x\z	0	1	2	3
x1	1	2	3	0
x2	2	3	0	0
x3	3	0	0	0

На пересечении i-той строки и j-того столбца ставится значение функции перехода.

При графической форме записи каждому состоянию соответствует отдельная вершина.