
- •“МОДЕЛИРОВАНИЕ СИСТЕМ”
- •Тема 1. Классификация моделей и виды моделирования
- •Моделирование, модель: свойства и назначение
- •Виды моделирования
- •Примеры материальных моделей
- •Идеальное моделирование
- •Место различных видов моделирования
- •Вопросы для самопроверки
- •Тема 2. Основные положения теории подобия
- •Подобные явления. Геометрическое подобие
- •Кинематическое подобие
- •Динамическое подобие
- •Теоремы подобия
- •Вопросы для самопроверки
- •Тема 3. Этапы математического моделирования
- •Алгоритм математического моделирования
- •Содержательная и концептуальная постановки задач моделирования
- •Математическая постановка задач моделирования
- •Качественный анализ и выбор метода решения
- •Реализация модели в виде программы
- •Вопросы для самопроверки
- •Тема 4. Моделирование на микроуровне
- •Понятие микроуровня
- •Основы построения ММ на микроуровне
- •Модели тепловых систем на микроуровне
- •Модели механических систем на микроуровне
- •Вопросы для самопроверки
- •Тема 5. Теория систем с распределенными параметрами
- •Базовые уравнения объектов с распределенными параметрами
- •Уравнения гиперболического типа
- •Уравнения параболического типа
- •Основное соотношение вход – выход
- •Функция Грина
- •Соединение распределенных блоков
- •Соединение распределенных блоков
- •Вопросы для самопроверки
- •Тема 6. Моделирование на макроуровне
- •Компонентные и топологические уравнения
- •Компонентные и топологические уравнения механической системы
- •Компонентные и топологические уравнения гидравлической системы
- •Компонентные и топологические уравнения тепловой системы
- •Компонентные и топологические уравнения электрической системы
- •Вопросы для самопроверки
- •Тема 7. Имитационное моделирование
- •Понятие имитационного моделирования
- •Виды имитационного моделирования
- •Подходы имитационного моделирования на шкале абстракции
- •Популярные системы имитационного моделирования
- •Вопросы для самопроверки
- •Тема 8. Методы упрощения моделей
- •Методы упрощения моделей
- •Вопросы для самопроверки
- •Тема 8. Программные и технические средства моделирования систем.
- •Классификация языков моделирования
- •Вопросы для самопроверки
- •ВОПРОСЫ К ЭКЗАМЕНУ ПО ДИСЦИПЛИНЕ «МОДЕЛИРОВАНИЕ СИСТЕМ»
- •20.Приближенные модели технических объектов на микроуровне. Метод конечных элементов.
- •43.Задачи качественного анализа ММ.

Вопросы для самопроверки
Какие выделяют этапы математического моделирования?
Что является результатом содержательной постановки задачи?
На каком этапе формируется перечень основных вопросов в терминах конкретных дисциплин?
Какие два класса выделяют среди математических соотношений? Какие уравнения называют равнениями состояния?
В чем заключается качественный анализ модели? Какие цели преследует проверка адекватности модели?
По каким причинам возможна неадекватность результатов моделирования?
Список литературы:
Тарасик В.П. Математическое моделирование технических систем: Учебник для вузов / В.П.Тарасик. – Мн.: ДизайнПРО, 2004.

Тема 4. Моделирование на микроуровне
Цель и задачи: изучить основные уравнения, описывающие тепловые, гидравлические и механические системы на микроуровне в виде сплошных сред.
Учебные вопросы:
4.1Понятие микроуровня
4.2Основы построения ММ на микроуровне
4.3Модели тепловых систем на микроуровне
4.4Модели гидравлических систем
4.5Модели механических систем на микроуровне

Понятие микроуровня
Микроуровень – нижний иерархический уровень, на котором осуществляется детальное описание физических свойств ТО (технические объекта).
Объекты рассматриваются, как сплошные среды, имеющие конечные области в трехмерном геометрическом пространстве
Общий вид уравнений модели микроуровня:
F(x , x ,...x , , |
д |
, |
д |
,..., |
д |
, |
д2 |
,... |
д ) 0 |
||
дx |
дx |
дx |
дх 2 |
||||||||
11 22 |
n |
|
|
|
|
дt |
|||||
|
|
1 |
|
2 |
|
n |
|
1 |
|
|
|
L (Z ) (Z )
L – дифференциальный оператор;
φ- искомая функция (фазовая координата) Z – вектор независимых переменных
Z - известная функция независимых координат
ГУ – сведения об искомых непрерывных функциях и (или) их производных на границе области определения объекта характеризующее
условия взаимодействия с окружающей внешней средой.
НУ – значения этих же функций во всей области определения в начальный момент времени, НУ задаются только при решения нестационарных задач.

Основы построения ММ на микроуровне
Закон сохранения: изменение во времени некоторой субстанций в элементарном объеме равна сумме притона – стока этой субстанций через его поверхность с учетом скорости генерации или уничтожения субстанций в этом объеме
д |
|
|
|
|
|
- фазовая переменная (координата) выражающая субстанцию; |
||||||||||||
|
|
|
|
|||||||||||||||
дt divI G |
||||||||||||||||||
|
G – вектор плоскости потока фазовой переменной; |
|||||||||||||||||
|
|
|
|
|
div I дивергенция вектора J; |
|
|
|
||||||||||
|
|
|
|
|
G – скорость генерации или уничтожения субстанций. |
|||||||||||||
Дивергенция вектора I : |
|
|
|
дIx |
|
дIy |
|
|
дIz |
|
|
|
||||||
divJ |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
дx |
дy |
|
дz |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Уравнение закона сохранения массы |
|
ρ - плотность массы; |
||||||||||||||||
д divI |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
I - вектор плотности потока массы. |
|||||||||||
|
|
|
|
|
|
|
||||||||||||
дt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Уравнение закона сохранения энергии |
|
|
д( E) |
|
|
|
||||||||||||
|
|
divIE GE |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
дt |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Уравнение закона сохранения количества движения
д( V ) |
|
|
grad |
Vdiv( V ) |
|||
д |
|
|
|

Модели тепловых систем на микроуровне
Уравнение теплопроводности на основе закона сохранения энергии: изменение во времени количество тепловой энергии в элементарном объеме равно сумме притока-стока энергии через его поверхность с учетом выделения энергии в том же объеме, в единице времени внутренними источниками (или поглощение энергии стоками).
divg GQ
Q- количество тепловой энергии в единицу объема
g- вектор плотности теплового потока
GQ - количество тепловой энергии, выделяемой в единицу времени в элементарном объеме
Изменение количества тепловой энергии |
dQ c dT |
||||
|
|
|
с - удельная теплоемкость материала; |
||
|
|
|
Ρ - плотность |
||
Плотность теплового потока q (закон Фурье) |
|
||||
q gradT |
λ - коэффициент теплопроводности материала |
||||
дТ |
|
1 |
div( gradT) GQ |
||
дt |
c |
||||
|
|
|
|||

|
Модели гидравлических систем на микроуровне |
||||||
Закон сохранения массы: |
Уравнение Навье – Стокса: |
||||||
д |
д( v) |
дv Gм |
1 |
дp |
4 |
д2v |
|
дx |
|
||||||
дt |
дt |
дx |
3 |
дx2 |
|||
Приближенная форма уравнения Навье – Стокса: |
Уравнение Эйлера: |
||||||
|
дv |
1 |
дp |
2 |
v |
|
|
||
|
|
|
|
||||||
|
дt |
дx |
|
|
|
||||
Уравнение состояния: |
Зависимость динамической |
||||||||
вязкости от температуры: |
|||||||||
|
p |
RT k 1n |
|||||||
|
0 |
T0 |
n |
||||||
|
|
||||||||
|
|
|
k |
|
|
|
|||
|
|
|
|
|
|
|
T |
|
|
дv |
|
1 |
дP |
|
4 |
|
д2v |
|||
|
дt |
|
|
|
|
3 |
|
дx |
2 |
|
|
||||||||||
|
|
дx |
|
|
|
|||||
|
д |
|
|
дv |
|
|
|
|
|
|
|
E |
|
|
|
|
|
||||
дt |
дx |
|
|
|
|
|
||||
дv 1 дp дt дx
Закон Гука:
д E дv дt дx
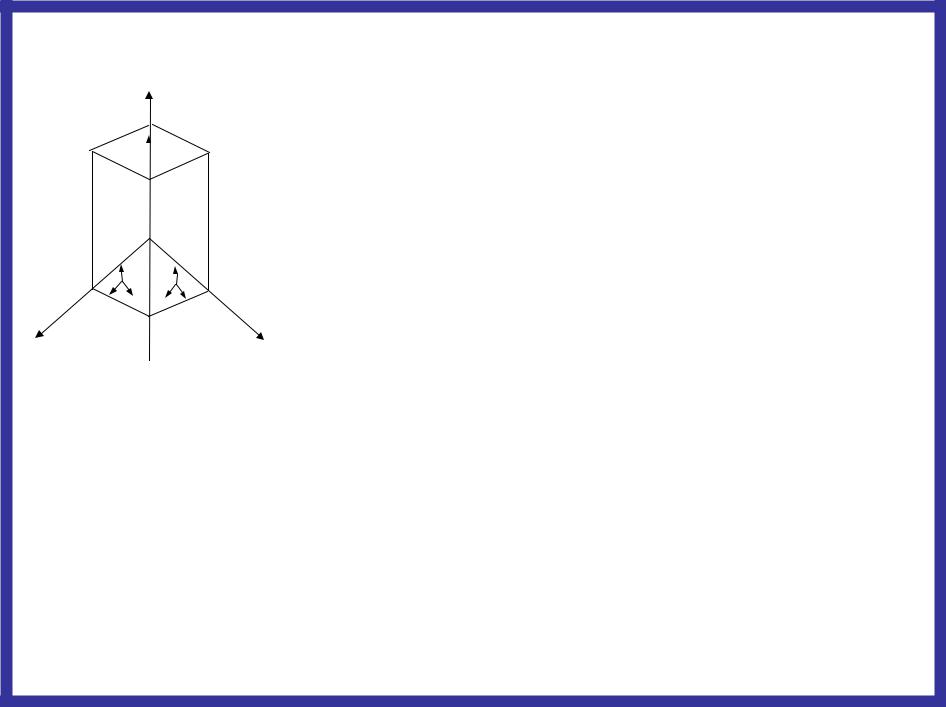
Модели механических систем на микроуровне
x3
33
13

 23
23
31 |
32 |
|
|
11 |
21 12 |
22 |
|
x1 |
|
|
|
Закон Гука:
Деформация:
Постоянные
Ламе:
Уравнение равновесия проекций на оси x1, x2, x3: |
|||||||||||||
|
2 |
|
3 |
д i |
gi |
ρ - плотность материала твердого тела; |
|||||||
|
д ui |
||||||||||||
|
дt |
i 1 |
|
дxj |
|
|
ui |
- перемещение элементов вдоль оси xi; |
|||||
|
|
ij |
- напряжения, действующее в направлении оси xi в |
||||||||||
|
|
gi |
гране элемента перпендикулярной оси xi; |
||||||||||
|
|
- проекция вектора массовых сил по ось xi; |
|||||||||||
x2 g- вектор ускорения свободного падения. |
|
||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
ii jj |
|
2 ii |
ij |
2 ij ,при |
i j |
|||||||
|
|
|
j 1 |
|
|
|
|
|
|
|
|
||
ij |
|
|
дu |
|
дu |
|
|
|
|
|
|
||
0.5 |
дx |
i |
дx |
i |
|
|
|
|
|
||||
|
|
|
j |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
i |
|
|
|
|
|
||
|
|
E |
|
|
|
|
|
6 |
|
|
E- модуль упругости; |
||
|
|
|
|
|
|
|
|||||||
1 1 |
|
2 |
|
2 1 |
υ- коэффициент Пуассона. |
||||||||
Основное уравнение теории упругости |
|
д2u |
|
2 |
|
|
grad divu |
u |
g |
||
(уравнение Ламе): |
|
дt2 |
|
|
|

Вопросы для самопроверки
1)Какие объекты понимаются под сплошными средами?
2)Какими уравнениями описываются системы на микроуровне?
3)Что называется фазовыми координатами?
4)Как звучит общая формулировка закона сохранения?
5)Каким выражением определяется дивергенция вектора I?
6)Какими уравнениями описываются закон сохранения массы, энергии и количества движения?
7)Какое уравнение называют уравнением неразрывности?
8)Какими способами может осуществляться теплообмен?
9)Как записывается уравнение теплопроводности?
10)Как рассчитывается коэффициент температуропроводности?
11)Как выглядит приближенная форма уравнения Навье – Стокса?
12)Как выглядит уравнение Ламе?
1. Список литературы:
Тарасик В.П. Математическое моделирование технических систем: Учебник для вузов / В.П.Тарасик. – Мн.: ДизайнПРО, 2004.

Тема 5. Теория систем с распределенными параметрами
Цель и задачи: освоить основные понятия теории систем с распределенными параметрами, основанные на элементах математической физики.
Учебные вопросы:
5.1. Базовые уравнения объектов с распределенными параметрами. Уравнения гиперболического, параболического и эллиптического типов.
5.2Общая характеристика условий однозначности: начальные и граничные условия.
5.3Основное соотношение вход – выход.
5.4Функция Грина.
5.5Стандартизирующая функция.
5.6Типовые распределенные блоки.
5.7Передаточные функции объектов СРП.
5.8Соединение распределенных блоков.

Базовые уравнения объектов с распределенными параметрами
L Q x,t f x,t , x D,t 0N Q x,t Q0 (x), x D,t 0Q x,t g(xi ,t), x D,t 0
Q x,t - функция состояния (выход объекта СРП) L - некоторый заданный оператор
f x,t - известная функция, характеризующая внешнее воздействие на процесс |
|
||||||
(вход объекта СРП) |
|
|
|
|
|
||
D - открытая часть области |
D, не содержащая границ |
|
|
|
|||
Q0 x - начальная функция, описывающая искомую функцию в замкнутой |
|
|
|||||
области в начальный момент времени. |
|
|
|
||||
N, Г - линейные операторы |
|
g x,t - граничные условия (второй вход объекта) |
|||||
D - граница области |
|
|
|
|
|
|
|
L Q x,t A x,t 2Q 2B x,t |
2Q |
C x,t 2Q A1 x,t Q B1 x,t |
Q |
|
|||
x t |
x |
||||||
t2 |
|
x |
t |
|
|||
C1 x,t Q f x,t |
|
|
Дискриминант: |
AC B2 |
|
|
|
|
|
|
|
|
|||
