7. Обратная матрица.

1. Обратная матрица

Обратная матрица(А^1)по отношению к исходнойА(квадратной) матрицематрица, для которой справедливы соотношения:

А^1А=ЕилиАА^1=Е(1)

На свойстве (1) базируется самая простая подпрограмма нахождения обратной матрицы

х₁,х₂, …, х_nстолбцы искомой обратной матрицы

Е₁, Е₂, …, Е_nсоответствующие столбцы единичной матрицы

т.е. необходимо nраз решить СЛУ относительно столбцов матрицыЕ.

2. Свойства обратной матрицы.

   1. (АВ^)1=В^1А^1

   2. (А^1)^Т=(А^Т)^1

   3. (А^1)^1=А

   4. det(A^1)=1det(A)

   5. Для диагональной матрицы

(2)

6. если исходная матрица является треугольной, то обратная есть треугольная того же вида.

7. Коррекция обратной матрицы при внесении в исходную матрицу некоторых возмущений (изменилось небольшое число элементов исходной матрицы, надо скорректировать обратную, не прибегая к новому обращению).

Лекция 8

8. Алгоритм сканирования

Если задана матрица А, и для нее известнаобратная матрицаА^1,

и если в исходную матрицу А внесены некоторые возмущения V, то обратную матрицу можно скорректировать, а не вычислять снова:

А  А^1



(А+V)  (A+V)^1

Возмущение (V)матрица вида:

если: ,(3)

внешнее (векторное) произведение

то (A+V) ^-1=A^1A^1VA^1, (4)

где =1/(1+) (5)

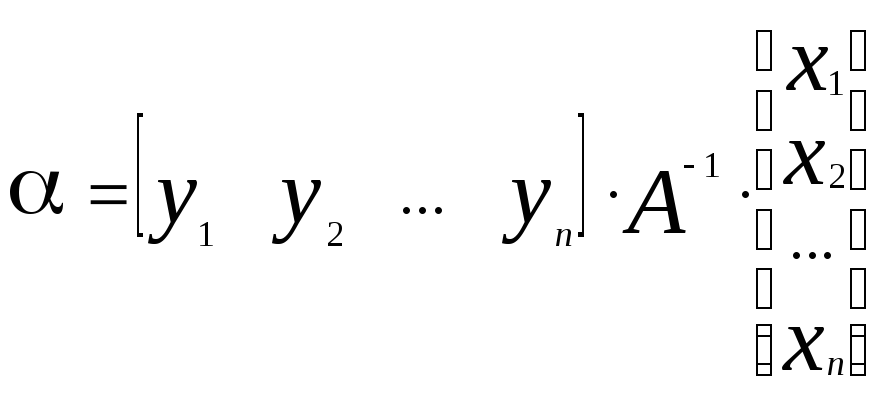(6)

в выражениях (4) (6) выполняется пересчет на базе уже известной матрицыА^1.

Допустим в исходную матрицу Авнесено возмущение (изменение) дляа_ijэлемента:

а^н_ij=а_ij+v_ij, н- новое значение

Надо скорректировать А^-1 , т.е. найти А^н1.

С учетом (3) возмущение можно представить в виде :

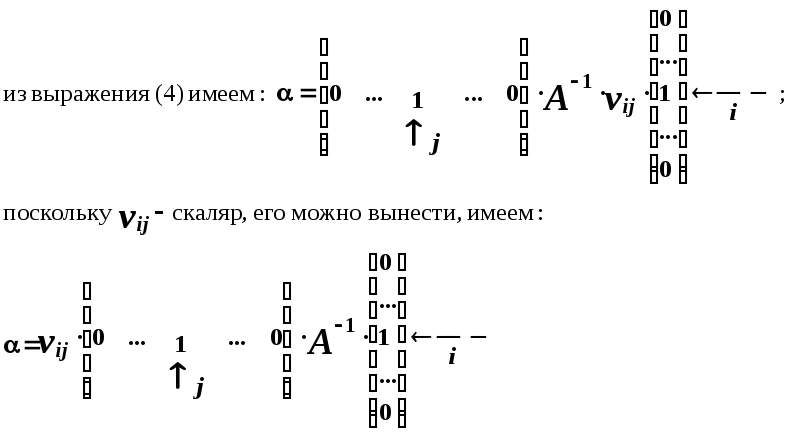
Алгоритм коррекции матрицы при изменении элемента a_ij

(метод сканирования):

1. Найти векторное произведениеiго столбца наjую строку. МатрицыА^-1:

2. Реализовать выражение (8).

Лекция 9

9. Обращение матрицы методом разбиения на блоки. Формулы Фробениуса.

1. Первая формула Фробениуса

Разобъем исходную матрицу Sна блоки

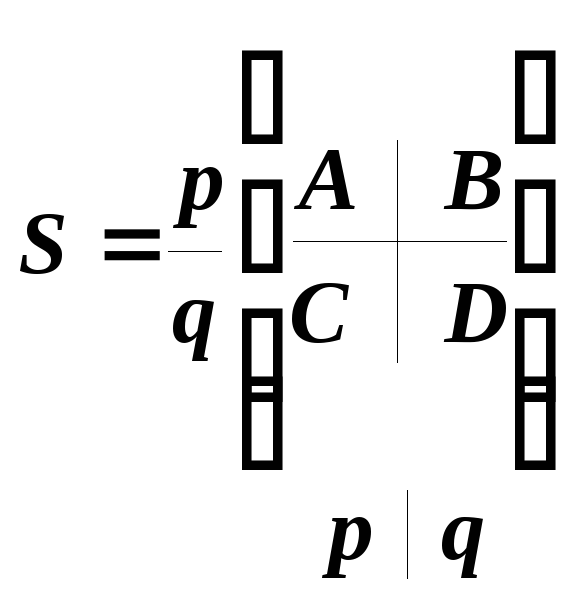
Соответственно искомая обратная матрица S^-1 будет иметь вид

из соотношения SS^1=E, гдеЕ – единичная матрица, имеем

(1)

Представим (1)в виде системы матричных уравнений:

AK+BM=E_p (2)

AL+BN=0 (3)

CK+DM=0 (4)

CL+DN=E_q (5)

Из (2)и(3)уравнения найдем матрицыKиL, домножиdэти уравнения на матрицуА^1слева

А^1АК+ВМ=Е

А^1АL+BM=0

K+A^1BM=A^1

L+A^1BN=0

K=A^1-A^1BM (6)

L= - A^1BN (7)

Подставим (6) и (7) соответственно в (4) и (5):

СA^1-СA^1BM + DM = 0 или (D-СA^1B)M = - СA^1

-C A^1BN + DN = E_q (D-СA^1B)N = E_q

Обозначив W=(D-СA^1B), имеем:

3. WM= - СA^1

4. WN= Eq

Откуда находим M, Nи подставляем в(6) и (7)

5. M= - W^-1СA^1 (8)

6. N= W^-1 (9)

результатом подстановки будут (10)и(11):

K=A^1+A^1BW^1CA^1 (10)

L=A^1BW^1 (11)

Подставляя (8),(9),(10),(11)в выражение дляS^-1 , окончательно получаем обратную матрицуS^1выраженную через блоки исходной матрицыS:

(12)

первая формула Фробениуса.

Где W=(DCA^1B)

Можно в общем виде показать справедливость этого выражения для чего исходную матрица Sможно умножить на S^-1.

2. Вторая формула Фробениуса.

Найдем из (4) и (5) M и N:

M= D^1CK (13)

N=D^1D^1CL (14)

Подставим выражения (13), (14) в (2), (3):

(A - BD^-1C)K=E

(A - BD^-1C L= - BD^-1

Обозначив V=(A - BD^-1C),(15)

имеем:

K=V^-1(16)

L= - V^-1 BD^-1 (17)

Подставим (16), (17)в выражения(13), (14),имеем:

M = -D^-1V^-1 (18)

N = D^-1 + D^-1CV^-1BD^-1 (19)

Выражения (15)  (19)определяютвторую формулу Фробениусаили в матричном виде:

(20)

вторая формула Фробениуса

где V=(ABD^1C)

Выводы:

1. Для реализации первой формулы Фробениуса(12)для матрицыS, имеющей размерностьp+q, достаточно обратить матрицуАразмерностиp, матрицуD размерности q, и выполнить ряд умножений матриц (понижаем размерность решаемой задачи).

2. Первая формула Фробениуса (12)используется в том случае, когда в исходной матрице известен блокА^1либо можно достаточно просто найтиА^1. Соответственно,вторая формула Фробениуса(20)используется, когда известен блокD^1либо легко образуется матрицаD.

3. На базе (12) и (20)формул Фробениусабазируется несколько важных частных случаев. Каждый частный случай представляет отдельный метод.

Лекция 10