Способы задания автоматов

Существует несколько способов задания F автоматов, но наиболее часто используется табличный, графический и матричный способы.

Табличный способ основан на использовании таблиц переходов и выходов, строки которых соответствуют входным сигналам автомата, а столбцы – его состояние.

Пример автомата Мили.

Xi	ZK
	Z0	Z1	Z2	…	ZK
	Переходы Z(t+1)
X1	φ(Z0, X1)	φ(Z1, X1)	φ(Z2, X1)	…
X2	φ(Z0, X2)	φ(Z1, X2)	φ(Z2, X2)	…
. . .
	Выходы
X1	Ψ(Z0, X1)	Ψ(Z1, X1)	Ψ(Z2, X1)	…
X2	Ψ(Z0, X2)	Ψ(Z1, X2)	Ψ(Z2, X2)	…
. . .

Xi	ZK
	Z0	Z1	Z2
	Переходы
X1	Z2	Z0		Z0
X2	Z0	Z2	Z1
	Выходы
X1	y1	y1	y2
X2	y1	y2	y1

,

,

.

При другом способе задания автомата используется понятие направленного графа.

Граф автомата представляет собой набор вершин, соответствующие различным состояниям автомата и соединяющих вершины дуг графа, соответствующие тем или другим переходам автомата.

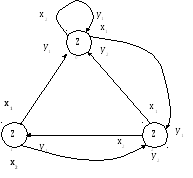
При матричном задание конечного автомата записывается квадратная матрица , строки которой соответствуют исходным состоянием, а столбцы состоянием перехода. Элемент, стоящий на пересеченииi-той строки и j-того столбца в случае автомата Мили соответствует входному сигналу Х_К, вызывающему переход из состояния Z_i в состояние Z_j и выдаваемые при этом в переходе.

Пример: для нашего случае.

.

Дискретно стохастические модели

Или Р-схемы описываются с помощью вероятностных автоматах (probabilistic automat).

В общем, виде вероятностный автомат можно определить преобразователь с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть записана статическими.

Введем понятие Р-автомата.

G – множество пар (х_i, Z_S), где х_i - элементы входного множества х;

Z_S – элементы подмножеств S;

Y – выходное подмножество;

В – подмножество вероятности переходов в состояние Z_K и появления на выходе y_j, если автомат был в состоянии Z_S и на вход поступил сигнал x_i.

.

Тогда схема Р, описывающая все перечисленные подмножества , называется вероятностным автоматом.

Как и в случае F-схемы существуют Р автоматы Мили и Мура.

Частотным случаем Р-автомата являются автоматы, у которых переход либо в новое состояние, либо выходной сигнал определяются детерминированием.

В первом случае автомат носит название Z- детерминированный вероятностным автоматом, во втором случае Y- детерминированный Р-автомат.

Для оценки различных характеристик исследуемых систем представляемых в виде Р-схем используются как аналитические модели, основанные на теории Марковских цепей, так и имитационные модели это метод статического моделирования.

Лекция № 5