Математические схемы моделирования Основные подходы к построению математической модели системы

Исходная информация при построении математической модели, процесса функционирования систем служат данные о назначении и условии работы исследуемой системы. Эта информация определяет основную цель моделирования систем S и позволяет сформулировать требования и разрабатываемой математической модели М.

Математическая схема – это звено, при переходе от содержательного к формальному описанию процесса функционирования процесса, с учетом воздействия внешней среды, т.е. имеет место цепочка: описательная модель → математическая схема → математическая модель.

Каждая система S характеризуется набором свойств, отражающих поведение системы и условия ее функционирования во взаимодействии с внешней средой ε.

Полнота модели регулируется в основном выбором границы системой S и внешней средой Е.

Задачу упрощения модели помогает выделить основные свойства системы, отбросив второстепенные.

Введем следующее обозначение:

1) Совокупность входных воздействий на систему

.

2) Совокупность воздействий внешней среды

.

3) Совокупность внутренних или собственных параметров системы

.

4) Совокупность выходных характеристик системы

.

В общем случае все переменные являются элементами подмножеств и содержат как детерминированные, так и стохастические состояния.

То есть, имеем следующую систему:

Экзогенные (независимые)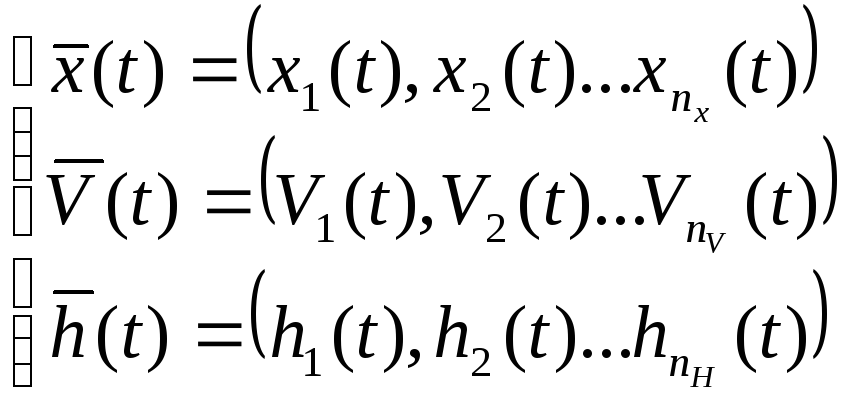

Эндогенные (зависимые переменные)

Процесс функционирования систем S в общем случае описывается во времени операторам F_S , который преобразует экзогенную переменную и эндогенную.

Для динамических систем:

(1)

Совокупность зависимостей выходных характеристик системы во времени y_i(t), , называется выходной траекторией, т.е. формула (1) называется законом о функционировании системы и позволяет получить выходную траекторию системы.

Закон функционирования F_S может, задан в виде функций логических условий в алгоритмических или табличных формах, в виде словесного описания.

Алгоритм функционирования A_S – это метод получения выходных характеристик, с учетом входных воздействий , воздействий внешней средыи собственных параметров системы.

Один и тот же закон функционирования F_S может быть реализован различными способами, т.е. с помощью различных алгоритмов A_S.

Для описания статических моделей:

(2)

Соотношение (1) и (2) может быть задано различными способами, например, в ряде случаев могут быть получены через свойства системы S в конкретные моменты времени, называемые состоянием системы.

Состояние системы характеризуется векторами:

,

,

где

,

,

,

,

в момент

,

,

,

и т.д., при

Если рассматривать процесс функционирования системы S как последовательность смен состояний , то они могут быть интерпретированы как коэффициенты точки к-мерной базового пространства, причем каждая реализация соответствует некой фазовой траектории.

Совокупность всех возможных значений состояний , называется пространством состояний, причем.

Состояние системы S в момент времени полностью определяется начальными условиями, выходными воздействиями, внутренними параметрамии воздействиями внешней среды, которые имели место за промежуток времени отдои описывается, с помощью следующих уравнений.

,

где

,

,

.

(3)

. (4)

Первое уравнение (3) по начальному состоянию и независимым переменнымопределяют вектор функции, а уравнение (4) по полученному значению состояниюопределяет зависимые переменные на выходе. Таким образом, цепочка уравнений объекта вход → состояние → выход, позволяет определить характеристику системы, описываемую уравнением (5).

(5)

В общем случае время в модели системы S может рассматриваться на интервале моделирования от 0 до Т, как непрерывное, так и дискретное, т.е. квантованное на отрезке временных единиц каждой, тогдаТ выражается , где- число интервалов дискретизации.