4.4 Модели гидравлических систем
В технических системах широкое применение находят гидравлические и пневматические приводы. При большой длине магистралей в них возникают волновые процессы, исследования которых осуществляют с исполнением ДУЧП.
Основные физические свойства жидкости и газа: текучесть, сжимаемость и непрерывность потоков. Текучесть оценивается вязкостью, сжимаемость – модулем объема упругости. Жидкости обычно имеют сравнительно большую вязкость и слабую сжимаемость, а газа наоборот. Тем не менее, математическое описание физических свойств жидкости и газа на микроуровне выполняется на основе одних и тех законов. Движение жидкости в трубопроводе обычно рассматривают, как одномерный сплошной поток. Для описания его движения вдоль координаты x используют закон сохранения массы, который выражает свойства непрерывного потока жидкости трубопроводе и записывается в виде:
(4.35)
Уравнение Навье – Стокса в одномерном случае выражающее закон сохранения количество движения элементарной массы имеет вид:
(4.36)
При анализе движения жидкости в трубопроводе обычно массовыми силами пренебрегают.
(4.37)
Находит также применение приближенная форма уравнения Навье – Стокса.
,
(4.38)
-
коэффициент линеаризованного вязкого
трения в трубопроводе.
Иногда при
исследовании пренебрегают вязкостью
жидкости. Принимая
=0,
выражение получаем уравнение Эйлера
для одномерного потока в трубопроводе
постоянного сечения.
(4.39)
Уравнение Эйлера учитывает лишь инерционное свойство потока, а уравнение Навье – Стокса – инерционное и диссипативные свойства (рассеивание энергии).
Сведем единую систему уравнения (4.35) и (4.37):
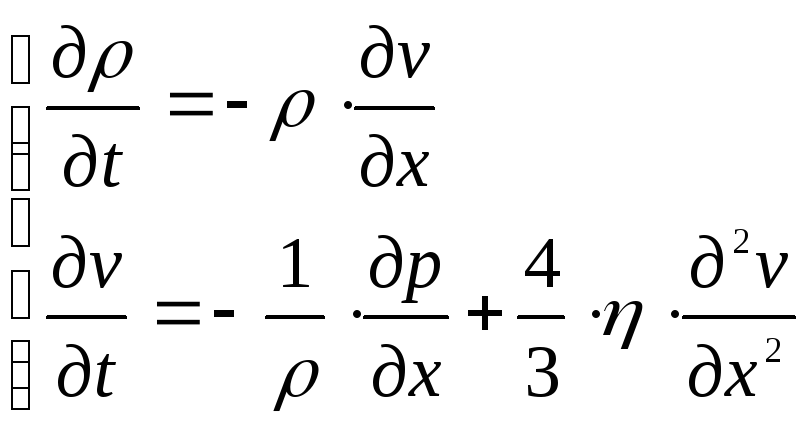(4.40)
Уравнение (4.40)
представляет системы нелинейных ДУЧП
с тремя неизвестными функциями: скорость
v,
давление p,
плотность
.
Чтобы сделать
систему определенной, необходимо в нее
добавить уравнения связи между
иp.
Будем полагать, что поток жидкости
изолирован от притока тепла извне
(адиабатический процесс). Для газа в
рассматриваемом случае плотность можно
выразить через давления на основании
уравнения состояния:
(4.41)
R – Газовая температура;
Т – температура;
k – Показатель ариобата
;
-
уравнение теплоемкости газа при
постоянном давлении и постоянном объеме
(Дж/к2*к).
-
энтальпия
Следует также учитывать зависимость динамической вязкости от температуры, обычно исследуют степенную зависимость вида:
(4.42)
При проектировании гидропривода часто принимают линейную аппроксимацию зависимости изменения давления от относительного изменения объема жидкости при ее стадии. Эта зависимость устанавливается законом Гука и в одномерном случае имеет вид:
(4.43)
E – Модуль объемной упругости жидкости.
Учитывая слабую
сжимаемость рабочей жидкости, полагают
и
для анализа полей скоростей используют
следующую систему ДУ:
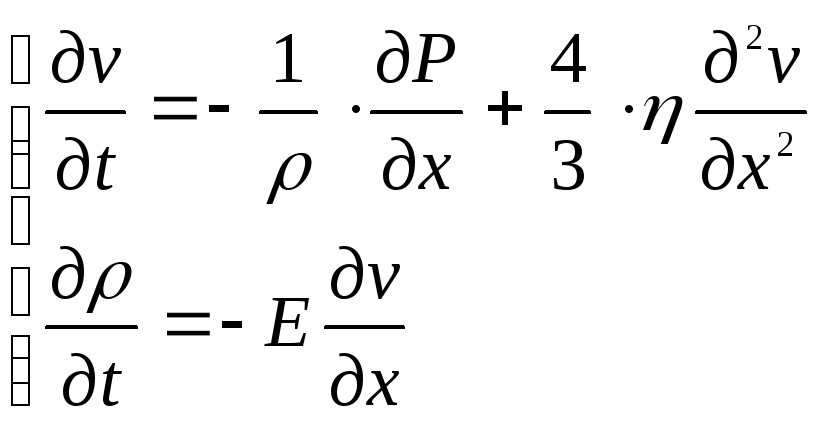(4.44)
Для решения систем уравнений (4.40), (4.44), необходимо задать краевые условия. Обычно принимают граничные условия первого рода и задают функции давления и скоростей на левую и правую границах участках трубопровода:
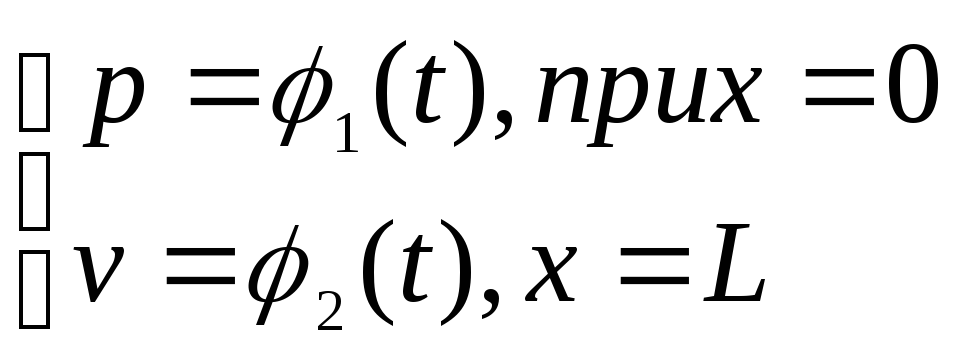(4.45)
НУ является значения этих же функций в начальный момент времени t=0 во всех контролируемых точках трубопроводах.