Тема 8. Методы упрощения моделей

Цель и задачи: ознакомится с основными методами упрощения моделей

Учебные вопросы:

1. Декомпозиция.

2. Метод макромоделирования

3. Метод линеаризации.

4. Упрощение модели с распределенными параметрами

При использовании сложной математической модели часто приходится ее упрощать с целью получения более простых методов анализа модели. Бывают обратные процессы, когда необходимо от простых моделей переходить к более сложным, чтобы получить большее соответствие между объектом-оригиналом и его моделью. В обоих случаях используются различные методы упрощения моделей. Рассмотрим основные из них.

1. Декомпозиция.

Декомпозиция – метод, заключающийся в расчленение сложной системы на ряд более простых подсистем.

Пусть имеется объект с вектором выходных параметров и векторами входных воздействий: управления,,, возмущения.

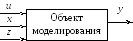
Декомпозиция возможна в том случае, если любой выход y_i не имеет связь с остальными выходами.

Целью декомпозиции является разбиение каждого пространства N, R, M, K на пространства меньших размерностей, в каждом из которых учитывается только связь данного выхода y_i с соответствующими переменными.

Если общая модель объекта имеет вид неявного выражения достаточно большой размерности

(1)

и выходы y_i с объекта не имеют связи между собой, то сложную модель (1) можно представить в виде совокупности эквивалентных ей n более простых частных моделей для каждого из выходов

  ,  (2)

где

2) Метод макромоделирования.

В данном методе в исходном пространстве переменных учитываются только те из них, которые влияют на выходные переменные наиболее сильно. Остальные неучтенные воздействия могут быть учтены в параметрической форме путем изменения коэффициентов при учтенных переменных, либо путем в ведения свободных членов.

3) Метод линеаризации.

Линеаризация исходной нелинейной модели облегчает решение конкретной задачи исследования. Поэтому для упрощения моделирования и исследования, когда это возможно, желательно заменить нелинейное уравнение приближенным линейным, решение которого с достаточной степенью точности описывает свойство исходной нелинейной системы. Процесс замены нелинейной модели линейной называется линеаризацией. Линеаризация может осуществляться путем замены нелинейной функции линейной типа y = a₀ + a₁x или, что чаще всего, путем разложения в ряд Тейлора.

4) Упрощение модели с распределенными параметрами.

Характеристики состояния объекта могут зависеть не только от времени, но и от пространственных координат. Из множества объектов с распределёнными параметрами можно выделить объекты, параметры которых приводимы к сосредоточенным. Это такие объекты, для которых достаточно знать значения входных и выходных переменных в конечном числе фиксированных точек пространства. Например, линейные объекты с распределёнными параметрами структурно могут быть представлены в виде многомерного линейного объекта с сосредоточенными параметрами. Тогда процессы в таких объектах будут описаны совокупностью математических моделей, определяющих изменения только во времени исследуемых выходных величин объектов в каждой фиксированной точке пространства.

 

Также упрощение моделей возможно и с помощью других способов, например, возможно пренебрежение динамическими свойствами процессов.

Вопросы для самопроверки

1) В чем заключается метод декомпозиции?

2) В каком случае возможна декомпозиция?

3) В чем заключается метод макромоделирования?

4) Какие вам известны методы линеаризации?

5) Как можно упростить модель с распределенными параметрами?

Список литературы:

1. Советов Б.Я. Моделирование систем. Учебник для ВУЗов / Б.Я. Советов, С.А. Яковлев. - М.: Высшая школа, 2001 г. – 343с.

2. Введение в математическое моделирование: Учеб. пособие / под ред. П.В.Тру-сова. – М.: Логос, 2005. – 440с.