5.4 Функция Грина

Если в краевой задаче (5.12) – (5.15) начальные условия нулевые, а граничные условия однородные, т.е. ;;;. А функцияв уравнении (5.12) представляется в виде

,

где - дельта – функция, зависящая оти сосредоточенная в точках

Т.о. (5.16) сводиться к виду

(5.17)

Т.е. функция Грина – решение краевой задачи при описанных выше условиях и описывает реакцию распределенной системы с нулевыми начальными и однородными граничными условиями в любой точке и любой момент временина точечное импульсное воздействие вида дельта – функции, применения в произвольной, но фиксированной точкев момент времени.

Функция Грина также называется фундаментальным решением (5.12), функцией точечного источника, импульсно – переходной функций.

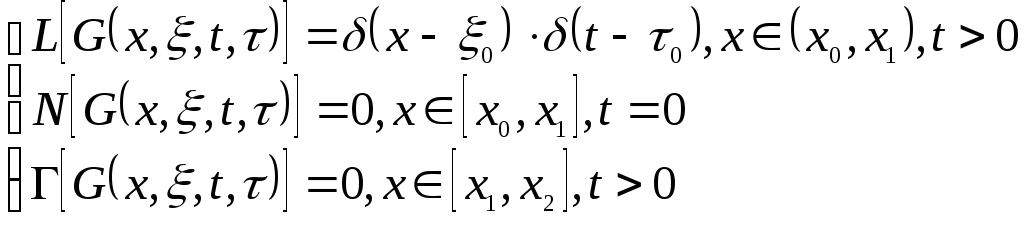
5.5 Стандартизирующая функция

В теории СРП можно подобрать такую функцию вместов уравнении (5.1) которое компенсирует эффект влияния на выходную величину нулевых начальных и неоднородных граничных условий и обеспечивает при этом равенство решенийисходной системы (5.1) – (5.3) и краевой задачи следующего вида:

(5.18)

Тем самым систему уравнений (5.18) эквивалентна исходной модели (5.1) – (5.3), но при этом, «собирая» правую часть к (5.1) все входные воздействия, существенно упрощает описание СРП.

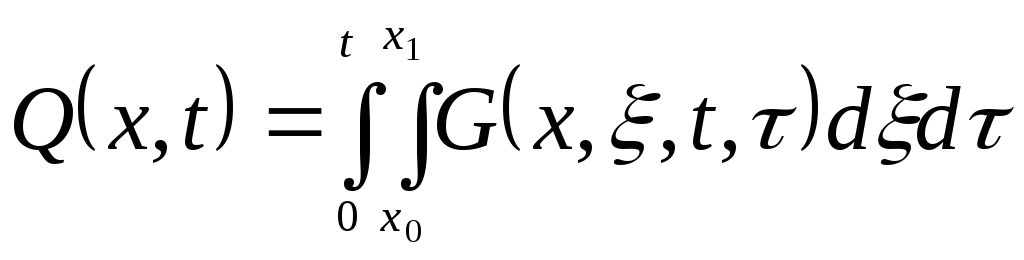(5.19)

(5.18) – стандартная форма (5.1)-(5.3)

(5.19) – интегральная форма

- стандартизирующая функция (нормирующая).

5.6 Типовые распределенные блоки

1) Переходной х-блок

Представляет собой распределенный блок с сосредоточенным входным и распределенным выходным сигналом. Это наиболее распространенный на практике вариант, для которого , где- фиксированный закон пространственного распределения на практике входного сигнала.

- изменяющаяся во времени составляющая входного сигнала.

2) Переходной -блок

Представляет собой распределенный блок сосредоточенными выходным и распределенный входным сигналом. В данном случае входное распределенное воздействие описывается стандартизирующей функцией , а сосредоточенный выход – значение функции состоянияв однойилификсированных точках.

(перебирает значения от 1 до).

Такие сосредоточенные выходы могут быть использованы в целях формирования соответствующих сигналов обратной связи при построении систем управления объектами с распределенными параметрами.

3) Переходной -блок

Распределенный блок с сосредоточенными входами и выходами. Моделирует поведение функции состояния объекта в фиксированных точкахпри сосредоточенном управлении.

4) Блок пространственного воздействия при фиксированных изменениях входного сигнала во времени

Не имеет аналогов в сосредоточенных системах. Для них стандартизирующая функция представляется в виде

;

5.7 Передаточные функции объектов срп

Применение для преобразования Лапласа по временному аргументу к выражению (5.19) позволяет распространить на СРП понятие передаточной функции и использовать методы, применяемые в ТАУ для линейных сосредоточенных систем.

В сосредоточенных системах:

(5.20)

(5.20) – континуальная передаточная функция.

Если удается из стандартизирующей функции выделить в явным виде компоненту входного воздействия,

то уравнение (5.19) с учетом (5.20)перепишется в виде

По возможности выносится входное возмущение в результате чего