Метод конечных разностей.

В САПР решение дифференциальных или интегро-дифференциальных уравнений с частными производными выполняется численными методами. Эти методы основаны на дискретизации независимых переменных - их представлении конечным множеством значений в выбранных узловых точках исследуемого пространства. Эти точки рассматриваются как узлы некоторой сетки, поэтому используемые в САПР методы - это сеточные методы.

Среди сеточных методов наибольшее распространение получили два метода: метод конечных разностей (МКР) и метод конечных элементов (МКЭ). Обычно выполняют дискретизацию пространственных независимых переменных, т. е. используют пространственную сетку. В этом случае результатом дискретизации является СОДУ для задачи нестационарной или система алгебраических уравнений для стационарной.

Метод конечных разностей исторически начал развиваться раньше МКЭ и является старейшим методом решения краевых задач.

Алгоритм МКР состоит из этапов, традиционных для метода сеток:

Этап 1. Построение сетки в заданной области. В МКР используется сетка, задаваемая конечным множеством узлов. В узлах сетки определяются приближенные значения искомой функции. Совокупность силовых значенийназываютсеточной функцией.

Этап 2. Замена дифференциального оператора в исходном дифференциальном уравнении известным аналогомL_h, построенным по одной из схем рассмотренных ниже. При этом непрерывная функция аппроксимируется сеточной функцией.

Этап 3. Решение полученной системы алгебраических уравнений.

При кажущейся простоте алгоритма МКР его практическая реализация наталкивается на ряд трудностей. Для выяснения их природы целесообразно рассмотреть основные этапы МКР более подробно.

Построение сетки в заданной области.

В МКР пользуются, как правило, регулярные сетки, шаг которых либо постоянен, либо меняется по несложному закону. Ниже на рис. 1 приведен пример построения сеток в МКР.

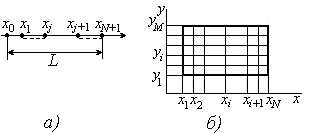
Рис. 1. Примеры построения сеток в МКР.

Для одномерных областей построение сеток мало чем отличается от аналогичной процедуры в МКР. Отрезок длиной L разбивается на N частей (рис. 1, а). Расстояние между двумя соседними узлами называется шагом сетки приi=1, 2, ..., N. При регулярной сетке шаг - постоянная величина, равная 1/(N-1), где N - количество узлов сетки.

Для двухмерной области подход к построению сетки существенно отличается от аналогичной процедуры в МКР. Пусть в качестве области изменения функции задан прямоугольник (рис. 1, б). Оси х и у разбиваются на отрезки, которые являются шагами сетки по соответствующим направлениям. Через точки деления проводятся прямые, параллельные осям координат. Совокупность точек пересечения (узлов) этих прямых и образует сетку в заданной двухмерной области. Соседними узлами такой сетки называются узлы, расстояния между которыми равно шагу сетки по одной из осей.

Способ построения сетки не меняется и в том случае, если задана область произвольной формы (рис. 1, в). Узлы сетки, попавшие внутрь области, называются внутренними узлами. Точки пересечения прямых, образующих сетку, с границей области называются граничными узлами.

Даже в случае постоянных шагов сетки по осям х и у в области имеются граничные узлы, отстоящие от ближайших к ним внутренних узлов на расстояние, меньшее шага по соответствующему направлению. Поэтому для двухмерной области произвольной формы сетка в общем случае всегда является нерегулярной, причем особенности геометрии учитываются только в околограничных узлах.

Замена дифференциального оператора разностным аналогом.

Эту процедуру легко проиллюстрировать на следующем простом примере. Пусть непрерывная функция , определенная на отрезке (рис. 1,а), описывается дифференциальным уравнением

(1)

где А - константа; задано также граничное условие и при дискретизации области была построена сетка с постоянным шагомh.

Заменим дифференциальный оператор разностным:

(2)

Где - правая разностная производная.

Подставив (2) в (1), получим разностное уравнение

(3)

Умножив (3) на h и полагая последовательность х=0, h, 2h, …, перейдем к системе алгебраических уравнений:

(4)

Решая (4) относительно сеточной функции, найдем таблицу значений, аппроксимирующую решение краевой задачи (1). При уменьшении шага h сетка становится все «гуще», а таблица значений сеточной функции - все подробнее. При неограниченном стремлении шага к нулю можно было бы получить значение искомой функции в каждой точке области. Но, в реальных случаях степень приближения к точному решению ограничивается рядом факторов, важнейшим из которых является размерность результирующей системы уравнений (4).

Для аппроксимации дифференциального оператора разностным кроме (2) часто пользуются выражением:

(5)

Где - левая разностная производная.

Кроме того, для аппроксимации , можно воспользоваться любой линейной комбинацией (2)-(5), т.е.

Где - любая вещественная константа.

При дифференциальный оператораппроксимируетсяцентральной разностной производной.

(6)

Подставив (6) в (1), получим другой разностный аналог краевой задачи (1):

.

Удобным геометрическим изображением схем построения разностных производных являются шаблоны.

На рис. 2 приведены шаблоны, соответствующие правой (рис. 2, а), левой (рис.2, б) и центральной (рис. 2, в) разностным производным.

Рис. 2. Примеры шаблонов в одномерной области, соответствующих разностным производным:а – правой,б– левой,в– центральной.

При переходе от дифференциальной краевой задачи к разностной необходимо также аппроксимировать граничные условия. В рассмотренном примере (1) граничные условия при использовании (2) можно аппроксимировать точно:

(7)

Совокупность разностного уравнения и разностных краевых условий называется разностной схемой краевой задачи.

В нашем примере уравнения (3) и (7) являются разностной схемой краевой задачи (1).

Кажущаяся простота построения разностной схемы в рассмотренном примере обманчива. В реальных задачах при построении разностных схем возникают проблемы. При исследовании разностных схем даже простых линейных задач часто выясняется, что разностная схема дает решение, не сходящееся при измельчении сетки к точному решению дифференциальной задачи. Поэтому построение сходящейся разностной схемы – центральный и наиболее сложный вопрос МКР.

Понятие сходимости разностной схемы тесно связано с понятиями точности и устойчивости.

Пусть точное значение непрерывной функции в узле с координатой x=x_h равно , а полученное значение точной функции в том же узле. Если погрешностьстремится к нулю при стремлении к нулю шагаh и имеет k-й порядок относительного шага, то принято говорить, что разностная схема имеет k-й порядок точности в n-м узле.

Аналогично для определения порядка аппроксимации вычисляют погрешность между точным и приближеннымзначениями производной вn-м узле:

При этом порядок погрешности относительно шага впадает с порядком аппроксимации дифференциальногоразностнымоператором вn-м узле.

Для определения порядка точности многих практических разностных схем достаточно определить порядок аппроксимации дифференциального оператора разности, так как порядки точности и аппроксимации для них совпадают. Однако разностная схема, для которой такое подтверждение может быть доказано, должна обладать еще одним важным свойством - устойчивостью.

Устойчивая разностная схема - схема, в которой не происходит наращивания малых ошибок округления, допущенных на начальных стадиях решения.

Для многих краевых задач сходимость разностной схемы является следствием аппроксимации ею краевой задачи и устойчивости. При этом порядок сходимости относительно шага совпадает с порядком аппроксимации.

Для гладких неразрывных функций хорошо развит математический аппарат изучения аппроксимации и доказательства устойчивости разностных схем.

Необходимость исследования сходимости впервые построенной разностной схемы обусловливает тот факт, что основу программных реализаций в САПР составляют вполне конкретные, хорошо изученные для определенных задач разностные схемы.