
- •6.4. Таблица номеров выполняемых заданий.
- •4. Методические указания по изучению дисциплины.
- •5. Материалы для контроля знаний студентов.
- •5.1. Задания для контрольной работы.
- •6. Приложения.
- •6.1. Образец решения контрольных задач типового варианта.
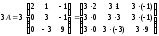
- •3А) Находим матрицу , обратную к , методом присоединённой матрицы, по формуле: , где:
6. Приложения.
6.1. Образец решения контрольных задач типового варианта.
1
– 10. Вычислить
определитель:

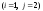
а)
непосредственным
разложением по
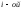 строке;
строке;
б)
непосредственным
разложением по
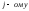 столбцу;
столбцу;
Решение.
а) вычисляем
определитель разложением по элементам
первой строки:
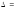
 =
=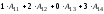 .
.
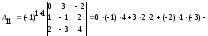
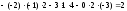
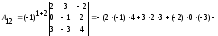
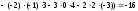
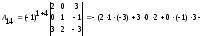
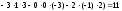
Тогда
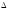 =
=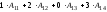 =
=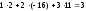
б)
вычисляем
определитель непосредственным разложением
по элементам второго столбца:
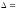
 =
=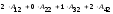 .
.
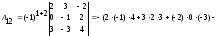
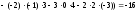
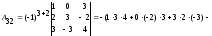
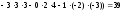
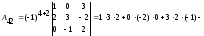
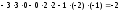
Тогда
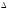 =
=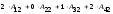 =
=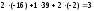 .
.
Ответ:
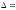
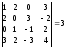 .
.
11-20.
Найти матрицу
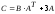 ,
если:
,
если:
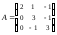 ,
,
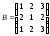 .
.
Решение:
1)
Транспонируем
матрицу
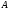 :
:
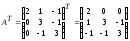 .
.
2)
Вычисляем
произведение матриц
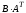 :
:
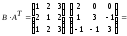

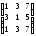 .
.
3)
Находим
матрицу
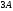 :
:
 .
.
4)
Находим
матрицу
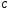 :
:
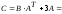
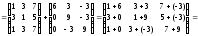
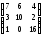 .
.
Ответ:
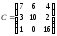 .
.
21-30.
Найти
собственные числа и векторы матрицы
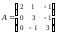 .
.
Множество
собственных чисел матрицы совпадает с
множеством корней характеристического
уравнения матрицы
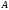 :
:
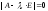 ,
а множество собственных векторов,
отвечающих собственному числу
,
а множество собственных векторов,
отвечающих собственному числу
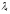 ,
совпадает с множеством ненулевых решений
матричного уравнения:
,
совпадает с множеством ненулевых решений
матричного уравнения:
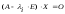 ,
определяемым методом Гаусса.
,
определяемым методом Гаусса.
Решение:
1)
Составляем характеристическое уравнение
матрицы
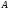 :
:
 .
.
Записываем его в виде алгебраического уравнения и находим действительные корни (среди них могут быть и кратные):
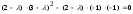
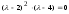
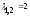 ,
,
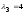 .
.
Таким
образом, собственными числами матрицы
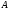 являются:
являются:
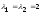 и
и
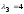 .
.
2)
Находим
собственные векторы матрицы
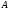 ,
отвечающие различным собственным числам
,
отвечающие различным собственным числам
 и
и
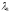 .
.
2.1)
Составляем
матричное уравнение
для нахождения
собственных векторов
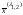 ,
отвечающих собственному числу
,
отвечающих собственному числу
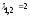 :
:
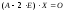
или
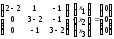
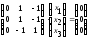 ,
,
записываем
его в виде системы линейных уравнений:
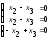 и решаем методом Гаусса. Полученная
система, очевидно, эквивалентна системе
и решаем методом Гаусса. Полученная
система, очевидно, эквивалентна системе
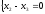 ,
имеющей специальный (трапециевидный)
вид. Такая система имеет бесконечно
много решений, которые записывают в
виде общего решения. Для записи общего
решения этой системы указываем её
базисные и свободные неизвестные.
Базисными являются неизвестные, столбцы
коэффициентов системы при которых
образуют базисный минор матрицы этой
системы. Такой минор образует, например,
столбец коэффициентов при неизвестной
,
имеющей специальный (трапециевидный)
вид. Такая система имеет бесконечно
много решений, которые записывают в
виде общего решения. Для записи общего
решения этой системы указываем её
базисные и свободные неизвестные.
Базисными являются неизвестные, столбцы
коэффициентов системы при которых
образуют базисный минор матрицы этой
системы. Такой минор образует, например,
столбец коэффициентов при неизвестной
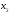 :
:
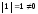 .
Поэтому выбираем в качестве базисной
– неизвестную
.
Поэтому выбираем в качестве базисной
– неизвестную
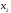 ,
тогда свободными будут неизвестные
,
тогда свободными будут неизвестные
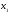 и
и
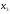 .
Свободным неизвестным придаём разные,
произвольные постоянные значения:
.
Свободным неизвестным придаём разные,
произвольные постоянные значения:
 ,
,
 ,
где
,
где
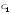 ,
,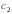
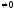 ,
одновременно, и выражаем через них
значение базисной неизвестной из
уравнения системы:
,
одновременно, и выражаем через них
значение базисной неизвестной из
уравнения системы:
 .
Тогда общее решение системы, задающее
множество всех собственных векторов
.
Тогда общее решение системы, задающее
множество всех собственных векторов
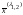 ,
отвечающих собственному числу
,
отвечающих собственному числу
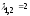 будет иметь вид:
будет иметь вид:
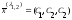 .
.
2.2)
Составляем
матричное уравнение
для нахождения
собственных векторов
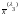 ,
отвечающих собственному числу
,
отвечающих собственному числу
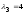 :
:
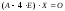
или
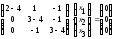

 ,
,
записываем
его в виде системы линейных уравнений:
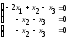 и решаем методом Гаусса. Полученная
система, очевидно, эквивалентна системе
и решаем методом Гаусса. Полученная
система, очевидно, эквивалентна системе
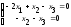 ,
имеющей специальный (трапециевидный)
вид. Система имеет бесконечно много
решений. Для записи её общего решения
указываем базисные и свободные
неизвестные. Базисный минор матрицы
системы образуют столбцы коэффициентов
при неизвестных
,
имеющей специальный (трапециевидный)
вид. Система имеет бесконечно много
решений. Для записи её общего решения
указываем базисные и свободные
неизвестные. Базисный минор матрицы
системы образуют столбцы коэффициентов
при неизвестных
 и
и
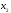 :
:
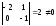 .
Поэтому выбираем в качестве базисных
– неизвестные
.
Поэтому выбираем в качестве базисных
– неизвестные
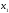 и
и
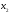 ,
тогда свободной будет неизвестная
,
тогда свободной будет неизвестная
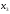 .
Свободной неизвестной придаём произвольное
постоянное значение:
.
Свободной неизвестной придаём произвольное
постоянное значение:
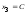 ,
где
,
где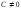 и выражаем через неё значения базисных
неизвестных
и выражаем через неё значения базисных
неизвестных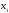 и
и
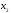 из уравнений системы специального
(трапециевидного) вида, начиная с
последнего уравнения:
из уравнений системы специального
(трапециевидного) вида, начиная с
последнего уравнения:
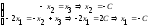 .
Тогда общее решение системы, задающее
множество всех собственных векторов
.
Тогда общее решение системы, задающее
множество всех собственных векторов
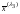 ,
отвечающих собственному числу
,
отвечающих собственному числу
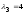 ,
будет иметь вид:
,
будет иметь вид:
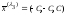 ,
,
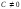 .
.
Ответ:
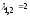 ,
,
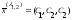 ,
,
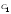 ,
,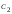
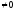 ;
;
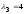 ,
,
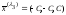 ,
,
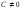 .
.
31
– 40. Дана
система уравнений:
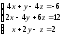 .
Требуется:
.
Требуется:
а) найти решение системы методом Крамера; б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса.
Решение.
А) Метод Крамера.
1а) Вычисляем определитель системы и проверяем, что он отличен от нуля:

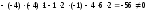 .
.
2а)
Так как
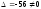 ,
то система имеет единственное решение,
определяемое формулами Крамера:
,
то система имеет единственное решение,
определяемое формулами Крамера:

3а)
Вычисляем определители
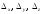 :
:
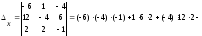
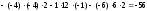 ,
,
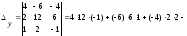
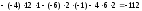 ,
,
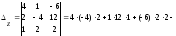
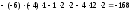 .
.
4а)
Находим решение:
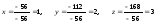 .
.
5а)
Выполняем проверку:
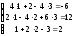
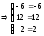 .
.
Ответ:
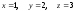 .
.
Б) Метод обратной матрицы.
1б) Записываем систему уравнений в матричном виде:
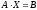 или
или
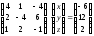
2б) Вычисляем определитель системы и проверяем, что он отличен от нуля:
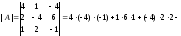
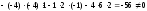
3б)
Так как
 ,
то матрица системы
,
то матрица системы
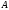 имеет обратную матрицу
имеет обратную матрицу
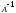 и единственное решение системы
определяется формулой:
и единственное решение системы
определяется формулой:
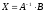 или
или
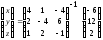
4б)
Находим
обратную матрицу
 (методом присоединённой матрицы):
(методом присоединённой матрицы):
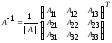 .
.
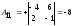
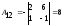
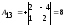
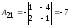
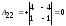
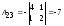

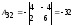
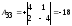
Тогда
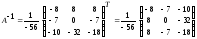 .
.
5б)
Находим
решение:

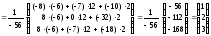 .
.
6б)
Выполняем проверку:
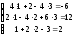
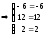 .
.
Ответ:
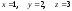 .
.
В) Метод Гаусса.
1в) Записываем расширенную матрицу системы:
 .
.
2в) Выполняем прямой ход метода Гаусса.
В
результате прямого хода матрица системы
 должна быть преобразована с помощью
элементарных преобразований строк к
матрице
должна быть преобразована с помощью
элементарных преобразований строк к
матрице
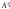 треугольного или трапециевидного вида
с элементами
треугольного или трапециевидного вида
с элементами
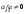 .
Система уравнений, матрица которой
.
Система уравнений, матрица которой
 является треугольной с элементами
является треугольной с элементами
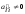
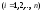 ,
имеет единственное решение, а система
уравнений, матрица которой
,
имеет единственное решение, а система
уравнений, матрица которой
 является трапециевидной с элементами
является трапециевидной с элементами
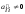
 ,
имеет бесконечно много решений.
,
имеет бесконечно много решений.
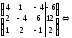


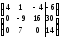



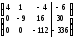 .
В результате
элементарных преобразований матрица
.
В результате
элементарных преобразований матрица
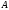 системы преобразована к специальному
виду
системы преобразована к специальному
виду
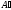 .
Система уравнений, матрица которой
.
Система уравнений, матрица которой
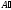 ,
является треугольной с ненулевыми
диагональными элементами
,
является треугольной с ненулевыми
диагональными элементами
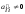 ,
имеет всегда единственное решение,
которое находим, выполняя обратный ход.
,
имеет всегда единственное решение,
которое находим, выполняя обратный ход.
Замечание.
Если при выполнение преобразования
расширенной матрицы
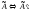 в преобразованной матрице
в преобразованной матрице
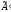 появляется строка
появляется строка
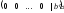 ,
где
,
где
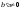 ,
то это говорит о несовместности исходной
системы уравнений.
,
то это говорит о несовместности исходной
системы уравнений.
3в) Выполняем обратный ход метода Гаусса.
Записываем
систему уравнений, соответствующую
последней расширенной матрице прямого
хода:
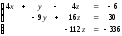 и последовательно из уравнений системы,
начиная с последнего, находим значения
всех неизвестных:
и последовательно из уравнений системы,
начиная с последнего, находим значения
всех неизвестных: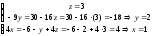 .
.
4в)
Выполняем проверку:

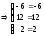 .
.
Ответ:
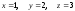 .
.
41-50. Найти общее решение для каждой из данных систем методом Гаусса:
а)
 .
.
Решение.
1а) Записываем расширенную матрицу системы:
 .
.
2а) Выполняем прямой ход метода Гаусса.

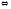
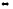





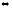





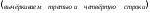


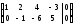 .
.
Матрица
системы приведена к трапециевидному
виду с ненулевыми диагональными
элементами. Соответствующая такой
матрице система уравнений имеет
бесконечно много решений, которые
находим, выполняя обратный ход, и
записываем в виде общего решения. Для
записи общего решения указываем её
базисные и свободные неизвестные.
Базисный минор матрицы системы образуют
столбцы коэффициентов при неизвестных
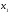 и
и
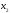 :
:
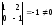 .
Поэтому выбираем в качестве базисных
– неизвестные
.
Поэтому выбираем в качестве базисных
– неизвестные
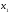 и
и
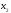 ,
тогда свободными будут неизвестные
,
тогда свободными будут неизвестные
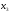 и
и
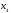 .
.
3а) Выполняем обратный ход метода Гаусса.
Записываем
систему уравнений, соответствующую
последней расширенной матрице прямого
хода:
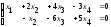 .
Свободным неизвестным придаём разные,
произвольные постоянные значения:
.
Свободным неизвестным придаём разные,
произвольные постоянные значения:
 ,
,
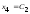 ,
и последовательно из уравнений системы,
начиная с последнего, находим значения
всех базисных неизвестных:
,
и последовательно из уравнений системы,
начиная с последнего, находим значения
всех базисных неизвестных:
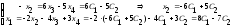 .
.
Тогда
общее решение системы запишется в виде:
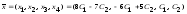 .
.
4а) Выполняем проверку:

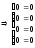 .
.
Ответ:
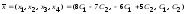 .
.
б)
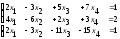 .
.
Решение.
1а) Записываем расширенную матрицу системы:
 .
.
2а) Выполняем прямой ход метода Гаусса.

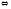

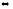

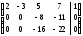

Замечание.
В результате прямого хода матрица
системы
 должна быть преобразована с помощью
элементарных преобразований строк к
матрице
должна быть преобразована с помощью
элементарных преобразований строк к
матрице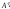 треугольного или трапециевидного вида
с элементами
треугольного или трапециевидного вида
с элементами
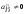 .
.
Если,
при выполнении преобразования расширенной
матрицы
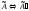 ,
в преобразованной матрице
,
в преобразованной матрице
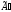 появляется строка
появляется строка
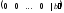 ,
где
,
где
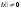 ,
то это говорит о несовместности исходной
системы уравнений.
,
то это говорит о несовместности исходной
системы уравнений.
Для
выполнения условия
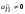 может
потребоваться перестановка местами
столбцов матрицы системы.
Если при
выполнении преобразований прямого хода
в матрице системы переставлялись местами
столбцы коэффициентов при неизвестных,
то в дальнейшем, при записи системы
уравнений, соответствующей последней
расширенной матрице прямого хода, это
следует учесть.
может
потребоваться перестановка местами
столбцов матрицы системы.
Если при
выполнении преобразований прямого хода
в матрице системы переставлялись местами
столбцы коэффициентов при неизвестных,
то в дальнейшем, при записи системы
уравнений, соответствующей последней
расширенной матрице прямого хода, это
следует учесть.












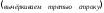


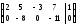 .
.
Матрица
системы приведена к трапециевидному
виду с ненулевыми диагональными
элементами. Соответствующая такой
матрице система уравнений имеет
бесконечно много решений, которые
находим, выполняя обратный ход, и
записываем в виде общего решения. Для
записи общего решения указываем её
базисные и свободные неизвестные.
Базисный минор матрицы системы, с учётом
перестановки местами столбцов, образуют
первый и второй столбцы коэффициентов
при неизвестных
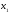 и
и
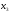 :
:
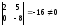 .
Поэтому выбираем в качестве базисных
– неизвестные
.
Поэтому выбираем в качестве базисных
– неизвестные
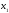 и
и
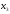 ,
тогда свободными будут неизвестные
,
тогда свободными будут неизвестные
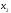 и
и
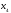 .
.
3б) Выполняем обратный ход метода Гаусса.
Записываем
систему уравнений, соответствующую
последней расширенной матрице прямого
хода:
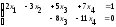 .
Свободным неизвестным придаём разные,
произвольные постоянные значения:
.
Свободным неизвестным придаём разные,
произвольные постоянные значения:
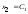 ,
,
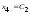 ,
и последовательно из уравнений системы,
начиная с последнего, находим значения
всех базисных неизвестных:
,
и последовательно из уравнений системы,
начиная с последнего, находим значения
всех базисных неизвестных:
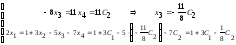 .
.
Тогда общее решение системы запишется в виде:
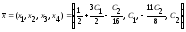
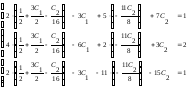
4б) Выполняем проверку:
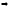
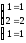
Ответ:
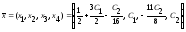 .
.
в)
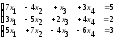 .
.
Решение.
1в) Записываем расширенную матрицу системы:
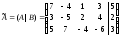 .
.
2в) Выполняем прямой ход метода Гаусса.







 .
.
При
выполнении преобразования расширенной
матрицы
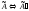 ,
в преобразованной матрице
,
в преобразованной матрице
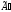 появилась строка
появилась строка
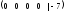 ,
соответствующая уравнению
,
соответствующая уравнению
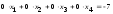 ,
которому не удовлетворяет ни один набор
значений неизвестных
,
которому не удовлетворяет ни один набор
значений неизвестных
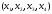 ,
что говорит о несовместности исходной
системы уравнений.
,
что говорит о несовместности исходной
системы уравнений.
Ответ: Система несовместна.
51 – 60. Исследовать квадратичную форму на знакоопределённость (по критерию Сильвестра).
а)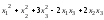 ;
б)
;
б)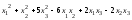
Решение.
1а)
Записываем
матрицу квадратичной формы:
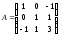 .
.
2а)
Проверяем является ли матрица
 невырожденной. Для этого вычисляем её
определитель
невырожденной. Для этого вычисляем её
определитель
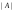 и проверяем, равен ли он нулю:
и проверяем, равен ли он нулю:
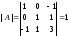 .
Так как
.
Так как
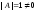 ,
то матрица
,
то матрица
 - невырожденная и, следовательно, для
исследования квадратичной формы на
знакоопределённость можно применить
критерий Сильвестра.
- невырожденная и, следовательно, для
исследования квадратичной формы на
знакоопределённость можно применить
критерий Сильвестра.
3а)
Вычисляем
угловые миноры матрицы
 и делаем вывод о знакоопределённости
квадратичной формы:
и делаем вывод о знакоопределённости
квадратичной формы:
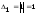 ,
,
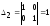 ,
,
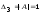 .
Так как выполняется условие:
.
Так как выполняется условие:
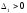 ,
,
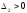 ,
,
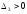 ,
то по критерию Сильвестра квадратичная
форма положительно определена.
,
то по критерию Сильвестра квадратичная
форма положительно определена.
Ответ: Квадратичная форма положительно определена.
1б)
Записываем
матрицу квадратичной формы:
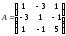 .
.
2б)
Вычисляем её определитель
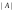 и проверяем, равен ли он нулю:
и проверяем, равен ли он нулю:
 .
Так как
.
Так как
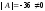 ,
то матрица
,
то матрица
 - невырожденная и, следовательно, для
исследования квадратичной формы на
знакоопределённость можно применить
критерий Сильвестра.
- невырожденная и, следовательно, для
исследования квадратичной формы на
знакоопределённость можно применить
критерий Сильвестра.
3б)
Вычисляем
угловые миноры матрицы
 и делаем вывод о знакоопределённости
квадратичной формы:
и делаем вывод о знакоопределённости
квадратичной формы:
 ,
,
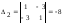 ,
,
 .
Так как два угловых минора нечётного
порядка имеют разные знаки:
.
Так как два угловых минора нечётного
порядка имеют разные знаки: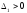 ,
, ,
то по критерию Сильвестра квадратичная
форма знакопеременна.
,
то по критерию Сильвестра квадратичная
форма знакопеременна.
Ответ: Квадратичная форма знакопеременна.
61
– 70. Даны
векторы
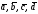 :
:
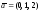 ;
;
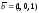 ;
;
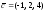 ;
;
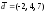 .
Требуется: а)
вычислить
скалярное произведение векторов
.
Требуется: а)
вычислить
скалярное произведение векторов
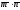 ,
если
,
если
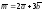 ,
,
 ;
б) вычислить
векторное произведение векторов
;
б) вычислить
векторное произведение векторов
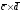 ;
в)
показать,
что векторы
;
в)
показать,
что векторы
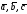 образуют базис
образуют базис
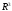 и найти координаты вектора
и найти координаты вектора
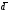 в
этом базисе.
в
этом базисе.
Решение.
1a). Находим вектор
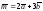
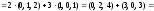
=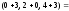
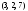 .
.
2а) Находим вектор
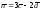
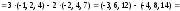
=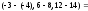
 .
.
3а)
Вычисляем
скалярное произведение
векторов
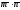 :
:
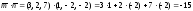 .
.
б)
Вычисляем
векторное произведение векторов
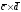 :
:
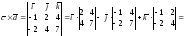
=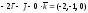
1в)
Покажем, что
векторы
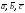 образуют
базис
образуют
базис
 .
Для этого
составим определитель, столбцами
которого являются координаты этих
векторов и покажем, что он отличен от
нуля.
.
Для этого
составим определитель, столбцами
которого являются координаты этих
векторов и покажем, что он отличен от
нуля.
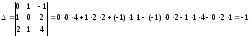 .
.
Так
как
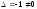 ,
то векторы
,
то векторы
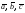 образуют
базис
образуют
базис
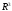 и, следовательно,
вектор
и, следовательно,
вектор
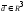 единственным образом можно разложить
по векторам этого базиса.
единственным образом можно разложить
по векторам этого базиса.
2в)
Записываем
разложение вектора
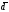 по векторам базиса
по векторам базиса
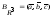 :
:
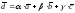 или
или
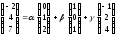 .
.
Коэффициенты
разложения
 ,
,
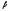 ,
,
 называют координатами вектора
называют координатами вектора
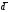 в базисе
в базисе
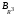 и записывают:
и записывают:
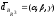 .
.
3в)
Записываем
векторное уравнение относительно
 ,
,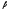 ,
, в виде эквивалентной ему системы линейных
уравнений:
в виде эквивалентной ему системы линейных
уравнений: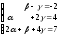 ,
и находим единственное решение системы,
например, по формулам Крамера:
,
и находим единственное решение системы,
например, по формулам Крамера:
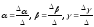 ,
где
,
где
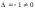 ,
,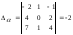 ,
, ,
, .
.
Таким
образом:
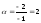 ,
,
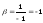 ,
,
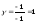 .
Следовательно, разложение имеет вид:
.
Следовательно, разложение имеет вид:
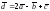 или кратко:
или кратко:
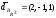 .
.
Ответ:
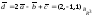 .
.
71-80.
Даны вершины
треугольника
 :
:
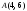 ,
,
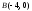 ,
,
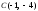 Требуется найти:
Требуется найти:
а)
длину стороны
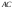 ;
б) уравнение
стороны
;
б) уравнение
стороны
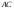 ;
;
в)
уравнение
медианы
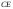 ,
проведённой из вершины
,
проведённой из вершины
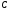 ;
;
г)
уравнение
высоты
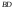 ,
проведённой из вершины
,
проведённой из вершины
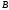 ;
;
д)
длину
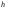 высоты
высоты
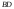 ;
е) площадь
;
е) площадь
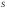 треугольника
треугольника
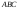 .
Сделать
чертёж.
.
Сделать
чертёж.
Решение. Сделаем чертёж:
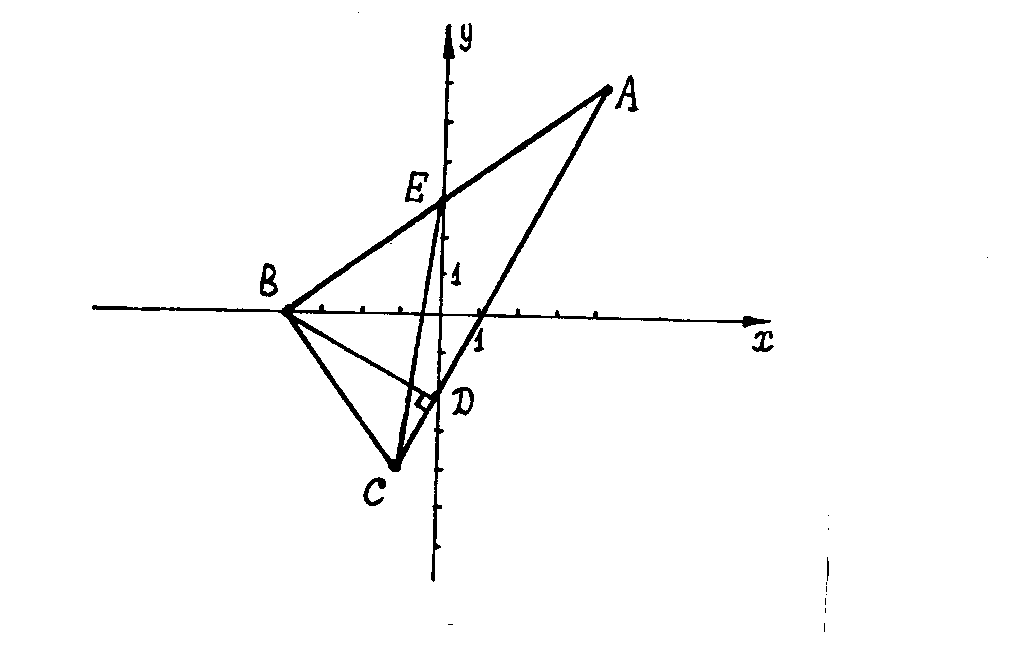
а)
Длину
стороны
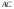 находим как
длину вектора
находим как
длину вектора
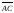 :
:
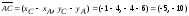 ,
,
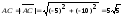 .
.
б)
Уравнение стороны
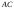 находим как уравнение прямой, проходящей
через точки
находим как уравнение прямой, проходящей
через точки
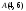 и
и
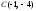 ,
и записываем его в виде общего уравнения
прямой:
,
и записываем его в виде общего уравнения
прямой:
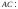
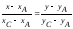
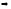
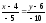
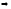
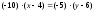
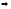
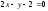 .
.
в)
Уравнение
медианы
 находим как уравнение прямой, проходящей
через точки
находим как уравнение прямой, проходящей
через точки
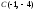 и
и
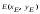 ,
и записываем его в виде общего уравнения
прямой. Неизвестные координаты точки
,
и записываем его в виде общего уравнения
прямой. Неизвестные координаты точки
 находим как координаты точки, делящей
сторону
находим как координаты точки, делящей
сторону
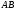 пополам:
пополам:
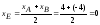 ;
;
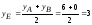 .
.
Тогда:
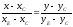
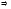
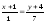
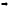
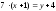

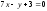 .
.
г)
Уравнение
высоты
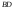 находим как уравнение прямой, проходящей
через точку
находим как уравнение прямой, проходящей
через точку
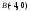 перпендикулярно вектору
перпендикулярно вектору
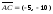 ,
который принимаем за нормальный вектор
прямой
,
который принимаем за нормальный вектор
прямой
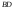 .
Тогда
.
Тогда
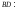
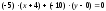
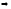

д)
Длину
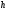 высоты
высоты
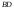 находим как расстояние от точки
находим как расстояние от точки
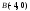 до прямой
до прямой
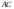 ,
заданной общим уравнением
,
заданной общим уравнением
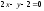 :
:
 .
.
е)
Площадь
треугольника
 находим по
формуле:
находим по
формуле:
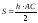 .
Откуда
.
Откуда
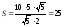 .
.
Ответ:
а)
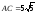 ;
б)
;
б)
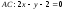 ;
в)
;
в)
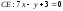 ;
;
г)
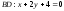 ;
д)
;
д)
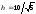 ;
е)
;
е)
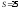 .
.
81
– 90. Даны
вершины пирамиды
 .
Требуется
найти:
.
Требуется
найти:
а)
длины ребер
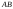 и
и
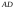 ;
б) угол
между ребрами
;
б) угол
между ребрами
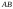 и
и
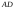 ;
;
в)
площадь
грани
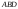 ;
г) объем
пирамиды
;
г) объем
пирамиды
 ;
;
д)
уравнение
плоскости грани
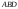 ;
;
е)
длину
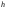 высоты
высоты
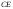 пирамиды
пирамиды
 .
.
Решение.
а)
Длины
рёбер
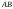 и
и
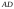 находим как
длины векторов
находим как
длины векторов
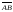 и
и
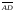 :
:
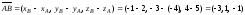 ;
;
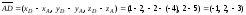 ;
;
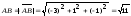 ;
;
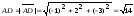 .
.
б)
Угол
 между рёбрами
между рёбрами
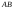 и
и
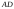 находим как
угол между векторами
находим как
угол между векторами
 и
и
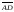 по формуле:
по формуле:
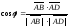 .
Учитывая, что:
.
Учитывая, что:
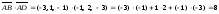 ,
,
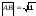 ,
,
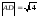 получим
получим
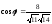 .
Откуда
.
Откуда
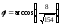
в)
Площадь
 грани
грани
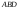 находим,
используя геометрический смысл векторного
произведения векторов, по формуле
находим,
используя геометрический смысл векторного
произведения векторов, по формуле
 .
Учитывая, что:
.
Учитывая, что:

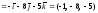 ,
,
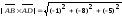 ,
получим
,
получим
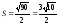 .
.
г)
Объём
 пирамиды
пирамиды
 находим,
используя геометрический смысл смешанного
произведения векторов, по формуле
находим,
используя геометрический смысл смешанного
произведения векторов, по формуле
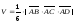 .
Учитывая, что:
.
Учитывая, что:
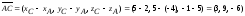 ,
,
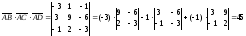 ,
,
получим
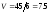 .
.
д)
Уравнение
плоскости грани
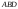 находим как уравнение плоскости,
проходящей через точки
находим как уравнение плоскости,
проходящей через точки
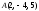 ,
,
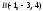 и
и
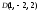 ,
и записываем его в виде общего уравнения
плоскости:
,
и записываем его в виде общего уравнения
плоскости:
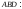
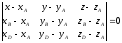
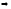
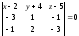
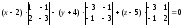
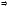
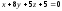
е)
Длину
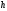 высоты
высоты
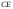 пирамиды
пирамиды
 находим как расстояние от точки
находим как расстояние от точки
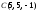 до плоскости
до плоскости
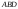 ,
заданной общим уравнением
,
заданной общим уравнением
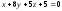 :
:
 .
.
Ответ:
а)
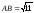 ,
,
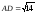 ;
б)
;
б)
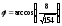 ;
в)
;
в)
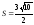 ;
;
г)
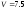 ;
д)
;
д)
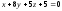 ;
е)
;
е)
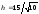 .
.
91–100. Установить, какую невырожденную кривую определяет алгебраическое уравнение второго порядка, построить её:
а)
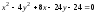 ;
б)
;
б)
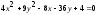 ;
;
в)
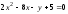 .
.
Решение:
а)
Так как
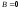 ,
,
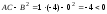 ,
то уравнение определяет гиперболу с
центром в точке
,
то уравнение определяет гиперболу с
центром в точке
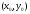 и осями симметрии, параллельными
координатным осям:
и осями симметрии, параллельными
координатным осям:
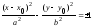 .
Вид кривой и расположение её на плоскости
известны. Выделяя полные квадраты в
левой части уравнения
.
Вид кривой и расположение её на плоскости
известны. Выделяя полные квадраты в
левой части уравнения
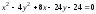 ,
преобразуем
его следующим образом:
,
преобразуем
его следующим образом:
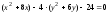
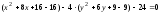

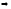
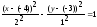 .
.
Полученное
уравнение определяет гиперболу с центром
в точке
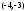 и осями симметрии параллельными
координатным осям. Для построения
гиперболы в системе координат
и осями симметрии параллельными
координатным осям. Для построения
гиперболы в системе координат
 :
1)
отмечаем центр гиперболы
:
1)
отмечаем центр гиперболы
 ;
2)
проводим через центр
;
2)
проводим через центр
 пунктиром оси симметрии гиперболы; 3)
строим пунктиром основной прямоугольник
гиперболы с центром
пунктиром оси симметрии гиперболы; 3)
строим пунктиром основной прямоугольник
гиперболы с центром
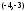 и сторонами
и сторонами
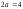 и
и
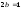 параллельными осям симметрии; 4)
проводим
через противоположные вершины основного
прямоугольника пунктиром прямые,
являющиеся асимптотами гиперболы, к
которым неограниченно близко при
бесконечном удалении от начала координат
приближаются ветви гиперболы, не
пересекая их; 5)
изображаем сплошной линией ветви
гиперболы (рис. 1).
параллельными осям симметрии; 4)
проводим
через противоположные вершины основного
прямоугольника пунктиром прямые,
являющиеся асимптотами гиперболы, к
которым неограниченно близко при
бесконечном удалении от начала координат
приближаются ветви гиперболы, не
пересекая их; 5)
изображаем сплошной линией ветви
гиперболы (рис. 1).
Ответ:
Гипербола
с центром в точке
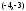 (см.
рис.1)..
(см.
рис.1)..
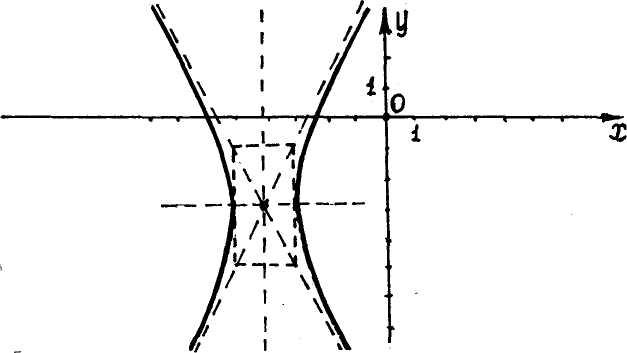
Рис.1
б)
Так как
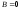 ,
,
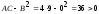 ,
,
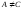 ,
то уравнение определяет эллипс с центром
в точке
,
то уравнение определяет эллипс с центром
в точке
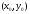 и осями симметрии, параллельными
координатным осям:
и осями симметрии, параллельными
координатным осям:
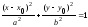 .
Вид кривой и расположение её на плоскости
известны. Выделяя полные квадраты в
левой части
.
Вид кривой и расположение её на плоскости
известны. Выделяя полные квадраты в
левой части
уравнения
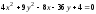 ,
преобразуем
его следующим образом:
,
преобразуем
его следующим образом:
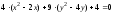
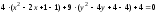
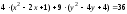
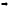
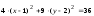
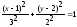 .
.
Полученное
уравнение определяет эллипс с центром
в точке
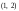 и осями симметрии параллельными осям
координат. Для построения эллипса в
системе координат
и осями симметрии параллельными осям
координат. Для построения эллипса в
системе координат
 :
1)
отмечаем центр эллипса
:
1)
отмечаем центр эллипса
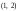 ;
2)
проводим через центр
;
2)
проводим через центр
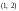 пунктиром оси симметрии эллипса; 3)
строим пунктиром основной прямоугольник
эллипса с центром
пунктиром оси симметрии эллипса; 3)
строим пунктиром основной прямоугольник
эллипса с центром
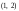 и сторонами
и сторонами
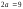 и
и
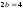 параллельными осям симметрии; 4)
изображаем сплошной линией эллипс,
вписывая его в основной прямоугольник
так, чтобы эллипс касался его сторон в
точках пересечения прямоугольника с
осями симметрии (рис.2).
параллельными осям симметрии; 4)
изображаем сплошной линией эллипс,
вписывая его в основной прямоугольник
так, чтобы эллипс касался его сторон в
точках пересечения прямоугольника с
осями симметрии (рис.2).
Ответ:
Эллипс с
центром в точке
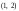 (см. рис.2).
(см. рис.2).
в)
Так как
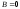 ,
,
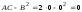 ,
,
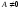 ,
то уравнение определяет параболу с
вершиной в точке
,
то уравнение определяет параболу с
вершиной в точке
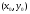 и осью симметрии, параллельной координатной
оси
и осью симметрии, параллельной координатной
оси
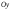 :
:
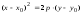 .
Вид кривой и расположение её на плоскости
известны. Выделяя полные квадраты в
левой части уравнения
.
Вид кривой и расположение её на плоскости
известны. Выделяя полные квадраты в
левой части уравнения
 ,
преобразуем
его следующим образом:
,
преобразуем
его следующим образом:
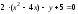
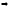
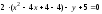
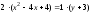
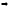
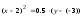
Полученное
уравнение определяет параболу с вершиной
в точке
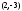 и осью симметрии параллельной оси
и осью симметрии параллельной оси
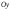 .
Для построения параболы в системе
координат
.
Для построения параболы в системе
координат
 :
1)
отмечаем вершину параболы
:
1)
отмечаем вершину параболы
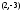 ;
2)
проводим через вершину
;
2)
проводим через вершину
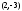 пунктиром ось симметрии параболы; 3)
изображаем сплошной линией параболу,
направляя её ветвь, с учётом того, что
параметр параболы
пунктиром ось симметрии параболы; 3)
изображаем сплошной линией параболу,
направляя её ветвь, с учётом того, что
параметр параболы
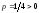 ,
в положительную сторону оси
,
в положительную сторону оси
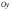 (рис.3).
(рис.3).
Ответ:
Парабола с
вершиной в точке
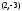 (см. рис.3).
(см. рис.3).
Рис.2. Рис.3.
101-110. Требуется: а) изобразить графически область решений системы неравенств; б) найти графическим способом решение задачи линейного программирования.
Решение.
1а)
Для построения
области решений строим в системе
координат
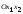 соответствующие заданным
ограничениям-неравенствам граничные
прямые:
соответствующие заданным
ограничениям-неравенствам граничные
прямые:
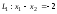 ,
,
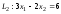 ,
,
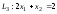 ,
,
 ,
,
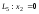 ,
,
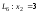 .
Прямая
.
Прямая
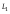 проходит через точки
проходит через точки
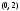 и
и
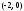 ;
;
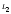 - через точки
- через точки
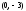 и
и
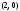 ;
;
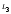 - через точки
- через точки
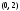 и
и
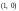 ;
;
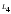 совпадает с осью
совпадает с осью
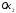 ;
;
 совпадает с осью
совпадает с осью
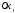 ;
;
 проходит через точку
проходит через точку
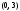 параллельно оси
параллельно оси
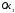 .
.
2а)
Находим
полуплоскости
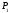 ,
,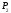 ,
,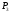 ,
,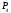 ,
,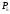 и
и
 в которых выполняются неравенства. Для
этого выбираем «пробную» точку и
проверяем, удовлетворяет ли она
ограничению-неравенству. Если
удовлетворяет, то данное неравенство
выполняется в полуплоскости, содержащей
«пробную» точку. В противном случае
берётся полуплоскость, не содержащая
«пробной» точки. В качестве «пробной»
точки выбирают любую точку, не принадлежащую
граничной прямой, например, начало
координат
в которых выполняются неравенства. Для
этого выбираем «пробную» точку и
проверяем, удовлетворяет ли она
ограничению-неравенству. Если
удовлетворяет, то данное неравенство
выполняется в полуплоскости, содержащей
«пробную» точку. В противном случае
берётся полуплоскость, не содержащая
«пробной» точки. В качестве «пробной»
точки выбирают любую точку, не принадлежащую
граничной прямой, например, начало
координат
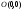 для нахождения полуплоскостей
для нахождения полуплоскостей
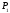 ,
,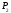 ,
,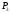 ,
,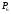 .
Полуплоскости,
в которых неравенства выполняются,
отмечаем стрелками, направленными
внутрь данной полуплоскости.
.
Полуплоскости,
в которых неравенства выполняются,
отмечаем стрелками, направленными
внутрь данной полуплоскости.
3а)
Строим
область решений
 как область, являющуюся пересечением
полуплоскостей
как область, являющуюся пересечением
полуплоскостей
 ,
отмечая её штриховкой (см. рис. 4).
,
отмечая её штриховкой (см. рис. 4).
Для
решения задачи линейного программирования
графическим способом: 1б)
Строим нормальный вектор
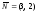 прямой
прямой
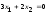 ,
являющейся линией уровня целевой функции
,
являющейся линией уровня целевой функции
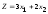 .
(вектор
.
(вектор
 показывает направление возрастания
значений целевой функции).
показывает направление возрастания
значений целевой функции).
2б)
Перпендикулярно
вектору
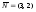 проводим пунктиром линию уровня
проводим пунктиром линию уровня
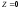 .
.
3б)
Параллельным перемещением линии уровня
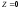 находим крайние точки области допустимых
решений
находим крайние точки области допустимых
решений
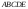 ,
в которых целевая функция достигает
минимума – точку
,
в которых целевая функция достигает
минимума – точку
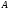 и максимума – точку
и максимума – точку
 .
.
4б)
Определяем координаты точек
 и
и
 .
Точку
.
Точку
 (точка пересечения прямых
(точка пересечения прямых
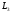 и
и
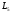 )
находим решая систему уравнений
)
находим решая систему уравнений
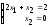 .
Откуда
.
Откуда
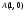 .
Точку
.
Точку
 (точка пересечения прямых
(точка пересечения прямых
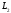 и
и
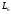 )
находим решая систему уравнений
)
находим решая систему уравнений
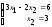 .
Откуда
.
Откуда
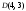 .
.
5б) Вычисляем:
 и
и
 .
.
Рис. 4
Ответ:
а) Область
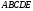 (см. рис.4)
(см. рис.4)
б)
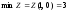 ;
;
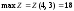 .
.
111-120.
Имеются
данные о работе трёх отраслей экономики
в отчётном периоде и план выпуска
конечной продукции
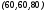 в следующем периоде (в усл. ден. ед.).
Требуется, используя модель Леонтьева
многоотраслевой экономики, найти: а)
матрицы коэффициентов прямых и полных
затрат; б)
плановые объёмы выпуска валовой продукции
каждой из отраслей, межотраслевые
поставки и объёмы выпуска чистой
продукции. В ответе записать данные
межотраслевого баланса планового
периода. (Указание:
значения коэффициентов прямых и полных
затрат вычислить с точностью до 0.01;
значения плановых объёмов выпуска
валовой и чистой продукции, межотраслевых
поставок округлить до целых значений).
в следующем периоде (в усл. ден. ед.).
Требуется, используя модель Леонтьева
многоотраслевой экономики, найти: а)
матрицы коэффициентов прямых и полных
затрат; б)
плановые объёмы выпуска валовой продукции
каждой из отраслей, межотраслевые
поставки и объёмы выпуска чистой
продукции. В ответе записать данные
межотраслевого баланса планового
периода. (Указание:
значения коэффициентов прямых и полных
затрат вычислить с точностью до 0.01;
значения плановых объёмов выпуска
валовой и чистой продукции, межотраслевых
поставок округлить до целых значений).
|
Отрасли производства |
Отрасти потребления |
Конечный продукт |
Валовой продукт |
||||
|
I |
II |
III |
|
|
|||
|
I |
20 |
25 |
105 |
50 |
200 |
||
|
II |
60 |
75 |
70 |
45 |
250 |
||
|
III |
60 |
50 |
140 |
100 |
350 |
||
|
Чистый продукт |
60 |
100 |
35 |
|
|
||
|
Валовой продукт |
200 |
250 |
350 |
|
|
||
Решение.
1)
Находим матрицу
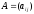 коэффициентов прямых затрат
коэффициентов прямых затрат
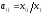 (
(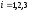 - номер отрасли производства,
- номер отрасли производства,
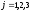 - номер отрасли потребления) и устанавливаем
её продуктивность:
- номер отрасли потребления) и устанавливаем
её продуктивность:
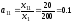 ,
,
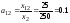 ,
,
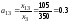
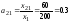 ,
,
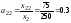 ,
,
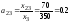
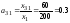 ,
,
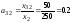 ,
,
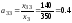 .
.
Таким
образом
 .
.
Так
как
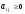 (
(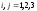 )
и
)
и
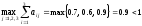 ,
то матрица
,
то матрица
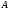 продуктивна и, следовательно, для любого
продуктивна и, следовательно, для любого
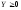 существует решение
существует решение
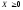 уравнения Леонтьева:
уравнения Леонтьева:
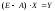 ,
записываемое в виде
,
записываемое в виде
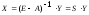 ,
где
,
где
 - единичная матрица,
- единичная матрица,
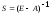 - матрица коэффициентов полных затрат,
- матрица коэффициентов полных затрат,
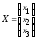 и
и
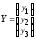 -
векторы (матрицы-столбцы) валового
выпуска и конечного продукта, соответственно
.
-
векторы (матрицы-столбцы) валового
выпуска и конечного продукта, соответственно
.
2а) Находим матрицу:
 .
.
