§8. Реалізація під-закону регулювання з не коливальною баластною ланкою.

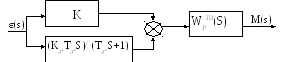
В основу такого ПІД-регулятора покладений ПІ-регулятор з не коливальною баластною ланкою, на його вхід подається сигнал розлагодження ε(s), та його похідна покажемо, що ця структура формує ПІД-закон регулювання:

Для цього запишемо еквівалентну передаточну функцію:

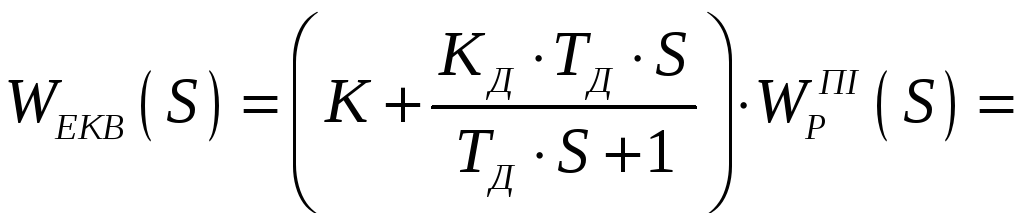замість реального ПІ-регулятора пишемо ідеальну передаточну функцію і баластну ланку

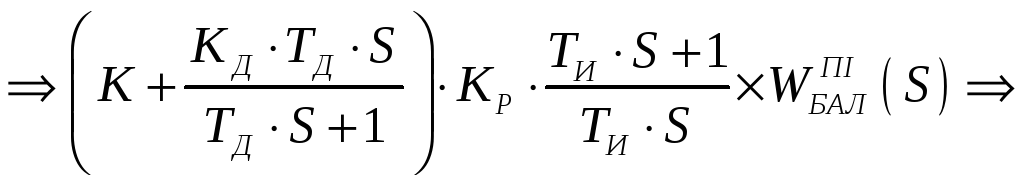
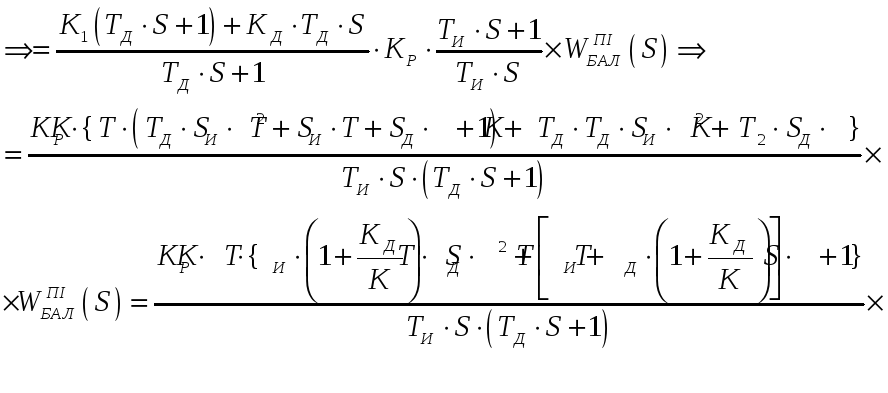
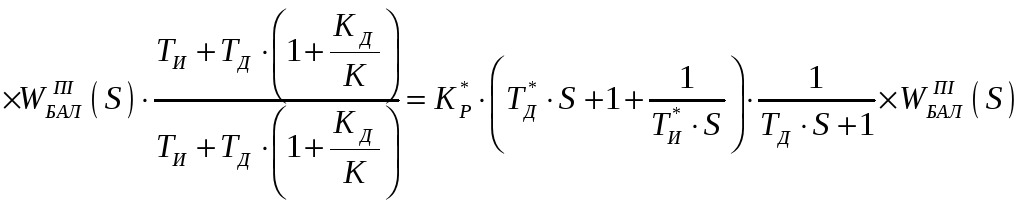
позначимо К_Р^*, Т_Д^* К_И^*, т.ч. отримаємо рівняння ПІД-регулятора.

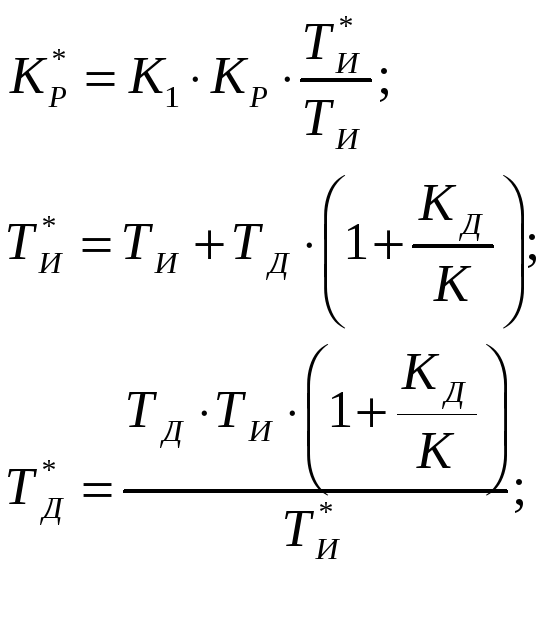
Висновок 1: і в цьому регуляторі параметри настройки взаємозв'язані.

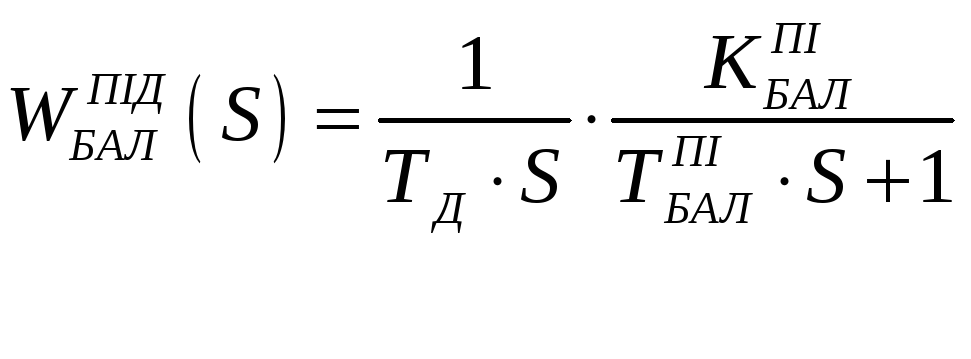
Висновок 2: передаточна функція баластної ланки має вигляд двох послідовних інерційних ланок, тобто вона є не коливальною аперіодичною, тому що корні характеристичного рівняння дійсні.

Висновок 3:відношення 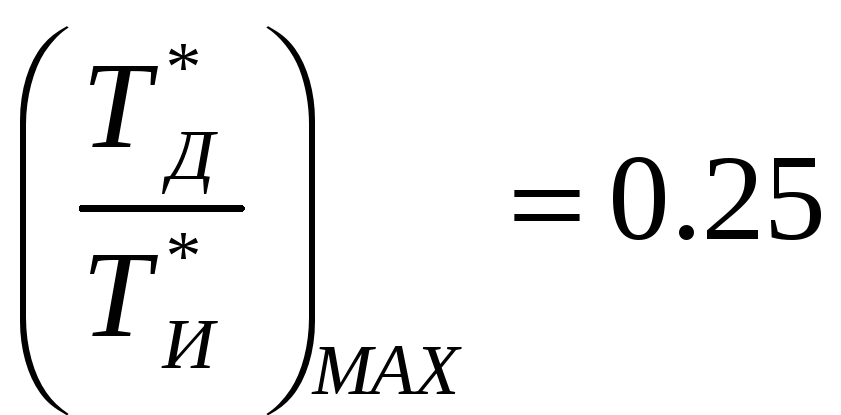при найгірших умовах .

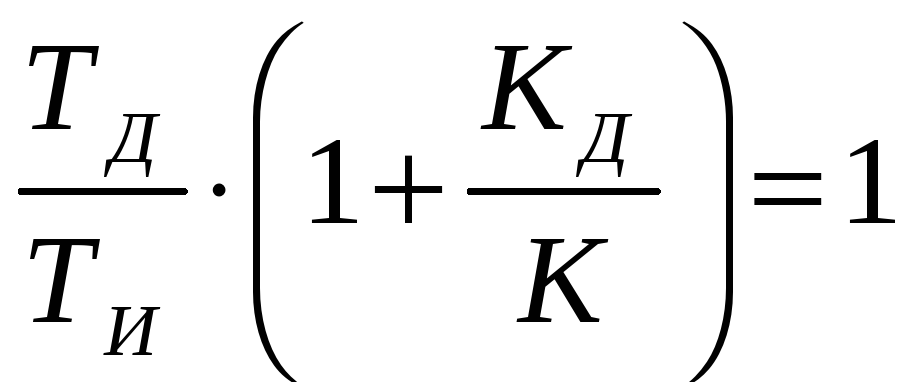Промислові ПІД-регулятори з аналоговими сигналами найчастіше будують за цією схемою.

§9.Промислові регулятори з нелінійними елементами.

В реальних умовах у складі автоматичного регулятора завжди є ланки з нелінійними характеристиками, такими типовими ланками є:

1. Нечутливість

Властива операційним підсилювачам, коли якійсь сигнал не підсилюється.

2. Обмеження – властиве вихідним сигналам підсилювача, в яких вихідний сигнал не може бути більше за напругу живлення. РО не можуть бути відкритими на 100%

0-100% – відкриття РО

3. Нечутливість з обмеженням

4. Ідеальне реле – властиве механічним реле з коефіцієнтом підсилення.

5. Люфт – властиве механічним редукторам в ВМ, в яких при реверсі шестерні деякий час переміщуються в повітрі до з’єднання з іншими шестернями.

6. Гістерезис – властиве елементам, що мають магнітні властивості (магнітні підсилювачі, соленоїди і ін.)

7. Трипозиційне реле – використовується в пускових пристроях у ВМ

Має 2 параметра: зона нечутливості ∆ та зона повернення ∆в

Загальним для цих та інших нелінійних характеристик є зміна коефіцієнта передачі в залежності від вхідного сигналу.

Коефіцієнт передачі може змінюватись від 0 до конкретного значення миттєво або скачко подібно, або з якоюсь швидкістю, залежно від амплітуди вхідного сигналу, тобто кожна з цих характеристик описується нелінійним алгебраїчним рівнянням.

Т.ч. наявність в структурі регулятора хоча б однієї нелінійної ланки робить його нелінійним.

Для таких регуляторів розглядають більш вузький діапазон роботи, що називають областю лінійної роботи.

Область лінійної роботи (ОЛР)– область у просторі амплітуди і частоти вхідного сигналу та параметрів настройки регулятора, в якій частотні характеристики нелінійного регулятора і його лінійної моделі (ідеальний регулятор) відрізняються не більше ніж на поперед задане значення.

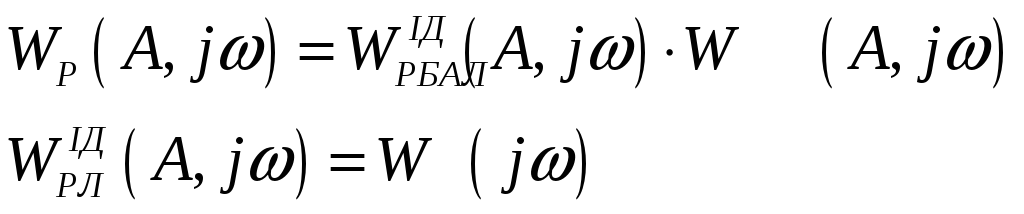
Якщо обмежити амплітуду і частоту вхідного сигналу, то в деякий області параметрів настройки такий регулятор буде працювати як звичайний ідеальний регулятор.

Властивості граничної системи дають можливість побудувати регулятори з властивостями ідеальних регуляторів у випадках охоплення і не охоплення нелінійної ланки F(x_л)

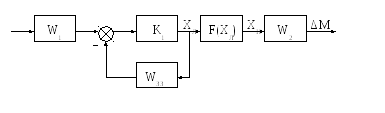
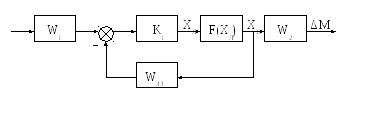
Ці всі інерційні ланки без інерційні, тобто миттєвої дії.

К₁ – коефіцієнт передачі операційного підсилювача,

∆W_ЗЗ – передаточна функція ланки зворотного зв’язку,

F(Х_Л) – розширена частотна характеристика нелінійної ланки,

Х_Л, Х_Н – сигнал з виходу, відповідно, лінійної і нелінійної ланок,

W₁ – передаточна функція нормуючого перетворювача (вона може бути і відсутня),

W₂ – передаточна функція ВМ.

Для того, щоб дослідити властивості нелінійного регулятора в граничній системі використовується гранична лінеаризація, яку розробив Попов.

В її основу покладена вібраційна теорія, яка дозволяє визначити гармонійний коефіцієнт лінеаризації нелінійного елемента.

Для цього Попов розклав рівняння нелінійного елементу в спеціальний ряд, перший елемент якого називається гармонічний коефіцієнт передачі.

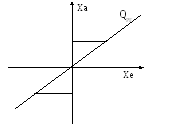
Т.ч. в ОЛР в разі виконання обмежень по амплітуді і частоті вхідного сигналу, поведінка нелінійного елемента близька до поведінки пропорційної ланки з відповідним коефіцієнтом передачі.

Для випадку а) можна записати еквівалентну передаточну функцію:

Висновок 1: в ОЛР в граничній системі властивості регулятора цілком визначаються передаточною функцією ланки зворотного зв’язку, тобто ми можемо формувати будь-який лінійний закон регулювання П, ПІ, ПІД, за рахунок підключення ланки зворотного зв’язку з потрібними властивостями.

Висновок 2: в реальному регуляторі, в якому К1 – якесь число, передаточна функція баластної ланки – інерційна ланка, тобто, якщо немає F(Х_Л), то настройки регулятора вибираються із ОНР, якщо немає ОЛР.

Висновок 3: ОЛР для регуляторів з нелінійністями значно менша, ніж ОНР, з цієї області визначаються настройки регулятора.

Для ПІД регулятора ОЛР буде мати наступні осі координат:

1. Амплітуда

2. Частота вхідного сигналу

3. Параметри нелінійного елементу (наприклад для трипозиційного реле – це зона нечутливості)

4. Зона повернення

5. Параметри настройки регулятора К_Р, Т_И, Т_Д

Або

1. А

2. Ω вхідні сигнали

3. ∆

4. ∆в нелінійні елементи

5. К_Р

6. Т_И автоматичний регулятор

7. Т_Д

Зображувати такий простір можна за допомогою перетинів фіксованих координат усіма координатами.

Промислові автоматичні регулятори мають параметри настройки нелінійного елементу і автоматичного регулятора, які градуїровані виходячи з обмежень на амплітуду і частоту. Тобто їх шкали побудовані для ОНР.