
- •§ 1. Функціональна схема системи управління.
- •§ 2. Автоматичні регулятори.
- •§ 3. Структура автоматичного регулятора.
- •§ 4. Класифікація промислових автоматичних регуляторів.
- •§5. Універсальні регулятори загально-промислового призначення.
- •§6. Розробники та виробники промислових регуляторів.
- •Глава 3
- •§1.Загальні принципи побудови регуляторів з лінійними типовими законами регулювання.
- •§2. Реалізація лінійних законів регулювання в автоматичних регуляторах з вм пропорційної дії.
- •§3. Реалізація лінійних законів регулювання в автоматичних регуляторах з вм постійної швидкості (метод послідовної корекції).
- •§4. Метод паралельної корекції при формуванні типових законів регулювання.
- •§5. Реалізація п-закону регулювання методом паралельної корекції.
- •§6. Реалізація лінійного пі-закону регулювання регулятором з вм постійної швидкості.
- •§7. Реалізація лінійного під-закону регулювання.
- •§8. Реалізація під-закону регулювання з не коливальною баластною ланкою.
- •§9.Промислові регулятори з нелінійними елементами.
- •§10 Основні режими роботи промислового автоматичного регулятора з вм постійної швидкості.
- •§11 Електричні засоби автоматичного регулювання.
- •§12. Загальні відомості про електричні системи тза.
- •§13. Функціональна схема електричних систем тза.
- •§14. Електрична уніфікована система приладів автоматичного регулювання під назвою "Каскад".
- •§15. Операційні підсилювачі системи "Каскад".
- •§16. Реалізація безпоштовхового перемикання із ручного в автоматичний режим.
- •§17 Регулюючи прилади системи "Каскад2"
§7. Реалізація лінійного під-закону регулювання.
а) з охопленням зворотнім зв’язком ВМ сталої швидкості:
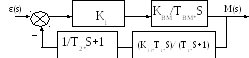
Лінійні закони регулювання використовують операції: множення, ділення, додавання, інтегрування, диференціювання.
К1 – операційний підсилювач (його наявність приводить до утворення граничної системи, якщо ЗЗ негативний).
Оскільки в прямому ланцюзі знаходиться операційний підсилювач, що охоплений негативним ЗЗ, то в граничній системі ПІД закон регулювання формується в ланці ЗЗ. Тому,
1 крок: визначимо передаточну функцію ланцюга ЗЗ, що формує ПІД закон:
Реальна диф. ланка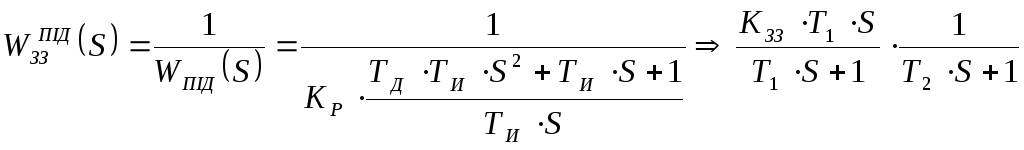




Основне рівняння
граничної системи
Інерційна ланка
Тут Т1 і Т2 – це постійні часу ЗЗ.
2 крок: для реального регулятора визначимо вигляд баластної ланки:
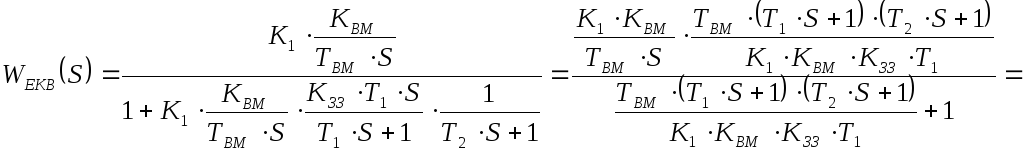
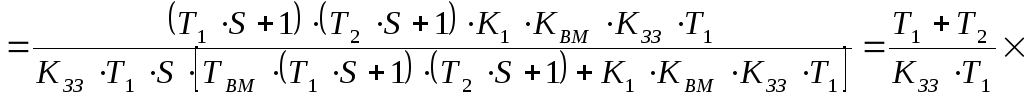
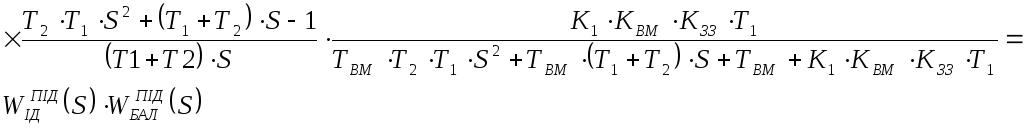
3 крок: аналіз властивостей реального ПІД-регулятора (коефіцієнт підсилення - якесь число):
1)Якщо позначити Т1+Т2 через параметр настройки ТИ, то одержимо передаточну функцію:
![]() ,
,
![]() ,
,![]() ,
,
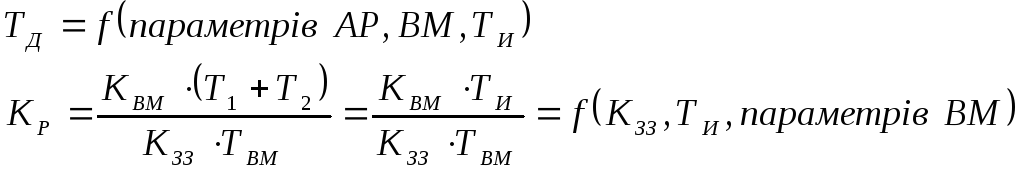
Висновок 1: параметри настройки ТД, ТИ, КР взаємозв’язані, ця залежність дуже погана, бо зміна одного з параметрів призводить до зміни інших.
Висновок 2: щоб позбутися взаємозалежності ТД, ТИ, КР потрібно використовувати операційні підсилювачі з максимальним коефіцієнтом К1.
-
Проаналізуємо властивості баластної ланки, для цього запишемо у такому вигляді (інерційної ланки другого порядку):
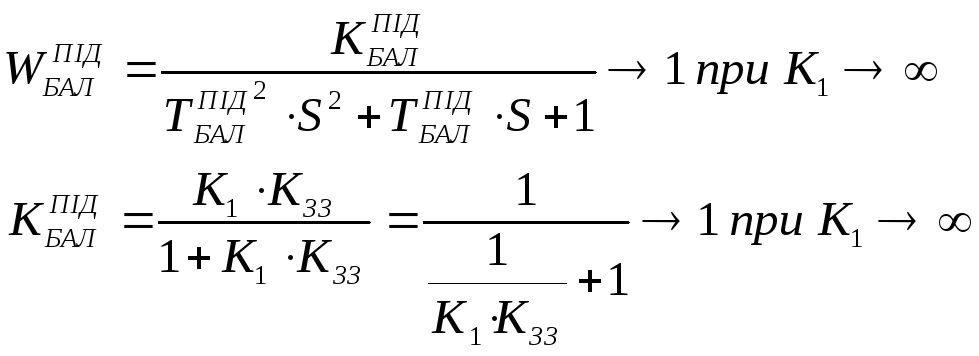
Висновок 1:
в граничній системі передаточна функція
баластної ланки наближається до
властивостей пропорційної ланки з
одиничним коефіцієнтом передачі,
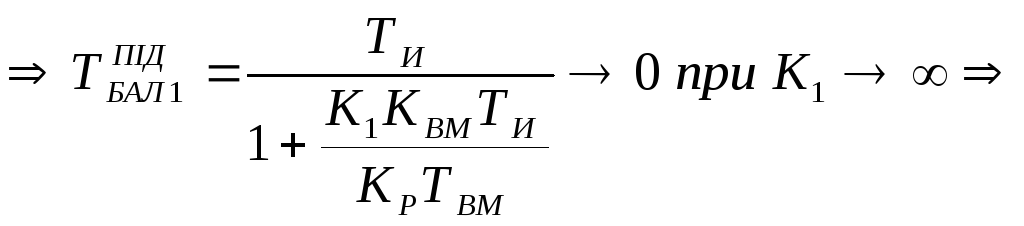 тому що коефіцієнт передачі в граничній
системі =1.
тому що коефіцієнт передачі в граничній
системі =1.
У виразі для
коефіцієнта передачі
![]() ,
К1
знаходиться і в чисельнику і в знаменнику,
це невизначеність виду
,
К1
знаходиться і в чисельнику і в знаменнику,
це невизначеність виду
![]() ,
оскільки для граничної системи можна
записати
,
оскільки для граничної системи можна
записати
![]() ,тому
використавши правило Лапіталя (для
цього і чисельник і знаменник ділимо
на К1)
ми переводимо невизначеність в чисельник.
Граничне значення К1
для
,тому
використавши правило Лапіталя (для
цього і чисельник і знаменник ділимо
на К1)
ми переводимо невизначеність в чисельник.
Граничне значення К1
для
![]() .
.
Висновок 2:
в реальному регуляторі при К1=const,
перша постійна часу
![]() ,
залежить від всіх параметрів, що в неї
входять, а саме
,
залежить від всіх параметрів, що в неї
входять, а саме
![]()
Друга постійна
часу в квадраті
![]() зв’язана з першою постійною часу
зв’язана з першою постійною часу
![]() через
вираз:
через
вираз:
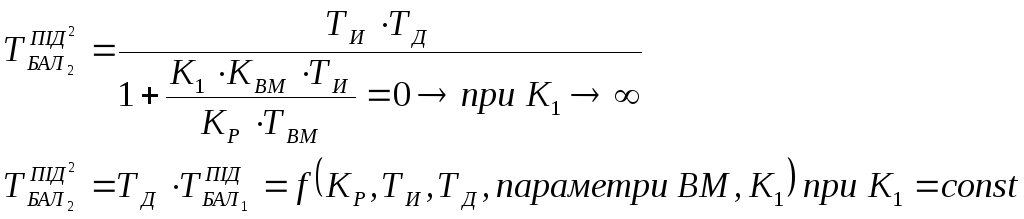
Висновок: постійні часу баластної ланки зв’язані між собою через параметр настройки регулятора ТД, тобто можливі таки ситуації, коли інерційна ланка другого порядку стає нестійкою.
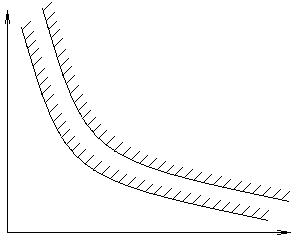
В залежності від співвідношення Т1 і ТБАЛ можливі 4 види кривих розгону інерційної ланки другого порядку:
Аперіодична (лише
дійсна)
Коливальна
затухаюча
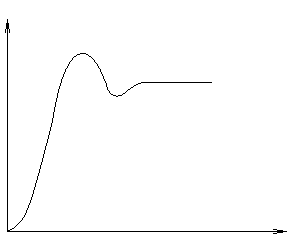
Автоколивальна
(1 дійсний корінь)
Нестійка (лише
уявна)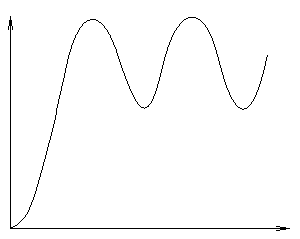
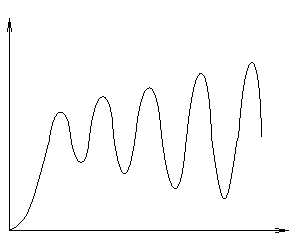
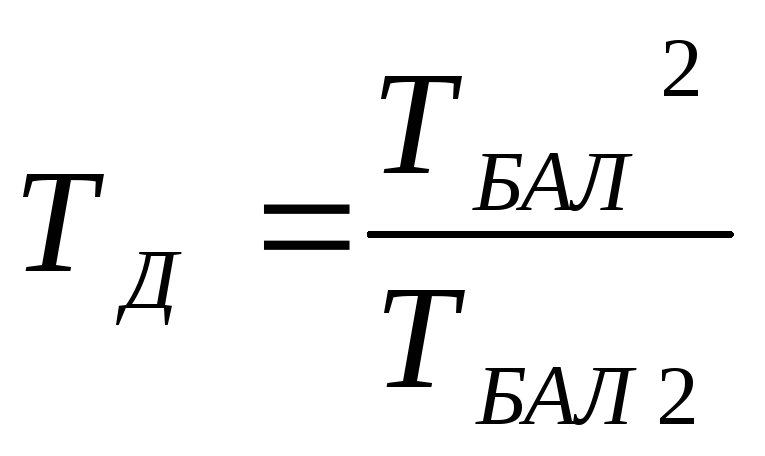
Висновок: в залежності від співвідношення ТБАЛ1 і ТБАЛ2 можливі стійкі і нестійкі перехідні процеси в баластній ланці, при чому вигляд залежить від ТД.
3)Визначимо граничне співвідношення між параметрами ТИ і ТД:
Як було показано раніше ТД і ТИ зв’язані між собою через Т1 і Т2, тому можна записати:
![]() ,оскільки
Т1
і Т2
входять і в чисельник і в знаменник,
тому визначимо найгірші умови:
,оскільки
Т1
і Т2
входять і в чисельник і в знаменник,
тому визначимо найгірші умови:
![]()
Висновок: максимальне співвідношення ТД/ТИ можливо лише при Т1=Т2, у інших випадках буде менше 0.25, тобто ТД/ТИ≤0.25.
Визначимо характеристики перехідних процесів у баластній ланці.
З дисципліни "Теорія автоматичного керування" відомо, що характер перехідного процесу залежить від коренів характеристичного рівняння.
Визначимо корені характеристичного рівняння.
Характеристичне рівняння будь-якої ланки записується шляхом дорівненя нулю знаменника передаточної функції і зміни оператора Лапласа на літеру "р":
![]()
Визначимо дискримінант квадратного рівняння, якщо корні дійсні, то ланка стійка, якщо корні уявні – ланка нестійка:
![]() Вираз у перший дужці завжди >0, тому
ми можемо проаналізувати вираз в другій
дужці :
Вираз у перший дужці завжди >0, тому
ми можемо проаналізувати вираз в другій
дужці :
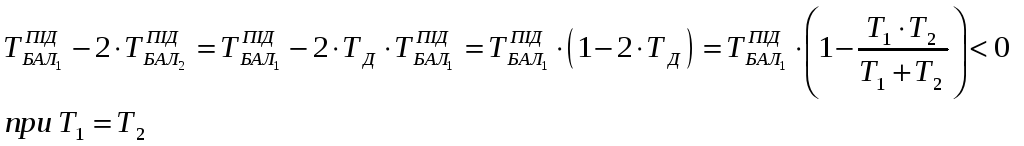
Т.ч. вираз у другій дужці завжди від’ємний при будь-яких Т1 і Т2.
Висновок: дискримінант характеристичного рівняння від’ємний, корні рівняння містять і реальну і уявну частину, тому крива розгону цієї баластної ланки – інерційна ланка з коливально-затухаючим перехідним процесом, відповідно крива розгону ідеального ПІ-регулятора буде
реальний
ідеальний
М t
КР/ТИ
КР
КД/ТИ
ОНР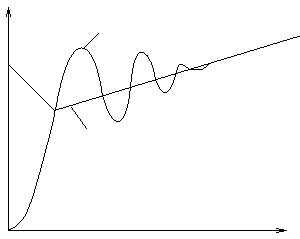
Висновок 1: при невеликих значеннях коефіцієнта К1 крива розгону ПІД-регулятора може бути коливальною, а при великих значеннях коефіцієнта К1 крива розгону буде близькою до ідеальної. Наша мета – використовувати високоякісні операційні підсилювачі.
ОНР для регулятора, у якого є три параметри настройки – це тривимірна фігура, її потрібно зображувати у трьох координатах КР, ТИ, ТД. Для того, щоб перейти до двовимірного зображення використовують накладання перерізів (перетинів) при фіксованих ТД . Для кожного значення ТД можна знайти дозволені значення КР, при яких ∆M(ω)<10%, а ∆Θ(ω)<15%
∆M(ω) – різниця між модулями КЧХ реального і ідеального ПІД-регулятора,
∆Θ(ω) – різниця між модулями фаз, а 10% і 15% - це границі.
Звідси і різниця між реальним і ідеальним регуляторами.
б) без охоплення зворотнім зв’язком ВМ сталої швидкості:
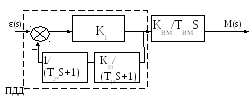
Оскільки ВМ не охоплений зворотнім зв’язком, і за своєю природою є інтегральною ланкою, то виходячи з методу послідовної корекції КПП повинен формувати ПДД2- закону (див. метод послідовної корекції).
Оскільки ми використовуємо граничну систему в КПП, то визначимо передаточну функцію ланцюга ЗЗ:
![]() якщо
винести за дужки КП
і позначити його як КЗЗ,
тоді в знаменник запишемо рівняння
другого порядку
якщо
винести за дужки КП
і позначити його як КЗЗ,
тоді в знаменник запишемо рівняння
другого порядку![]() ,
т.ч. можна стверджувати, що в ЗЗ граничної
системи потрібно встановити інерційну
ланку другого порядку, що має аперіодичну
криву розгону:
,
т.ч. можна стверджувати, що в ЗЗ граничної
системи потрібно встановити інерційну
ланку другого порядку, що має аперіодичну
криву розгону:
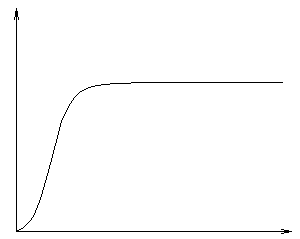
2)Визначимо властивості реального ПІД-регулятора, для цього запишемо еквівалентну передаточну функцію:

Проаналізуємо властивості одержаного ПІД-регулятора:
1)Якщо взяти вираз для ідеального ПІД-регулятора, то видно, що ТИ=Т1+Т2 –постійна часу інерційної ланки,
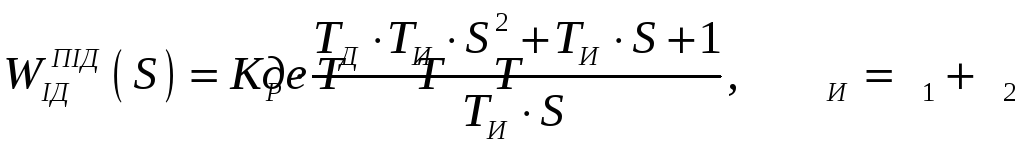
а раз це так, то КР залежить від ТИ і інших параметрів регулятора, що не є гарною рисою регулятора:
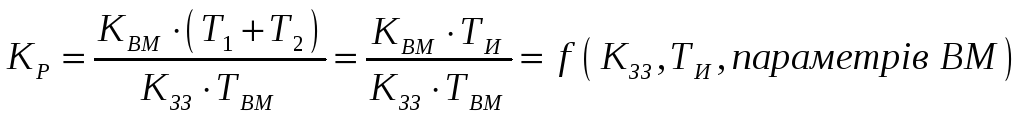
Аналогічно, параметр настройки ТД жорстко залежить від КР і ТИ:
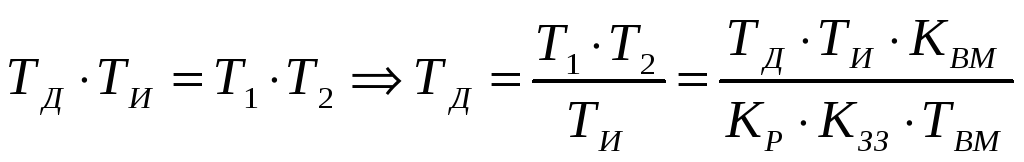
Висновок: всі параметри настройки КР , ТИ, ТД між собою пов’язані, або, змінивши один параметр, автоматично зміняться інші.
2) Проаналізуємо властивості баластної ланки (наскільки вона спотворює закон регулювання):
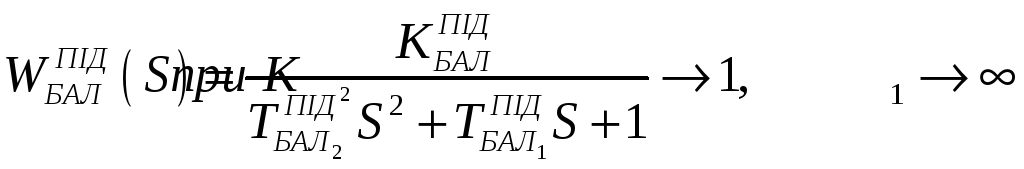
Баластна ланка – це інерційна ланка другого порядку, яка може бути аперіодичною, коливальною, нестійкою, залежно від коренів характеристичного рівняння:
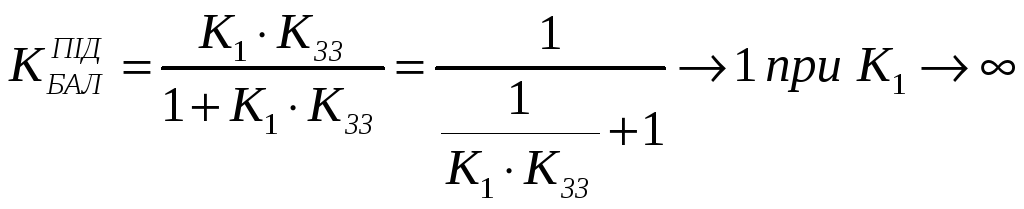
Коефіцієнт передачі баластної ланки, якщо використати правило Лапіталя, наближається до одиниці, тобто баластна ланка не змінює амплітуду регулювального сигналу. Запишемо рівняння для ТБАЛ1 і ТБАЛ2:
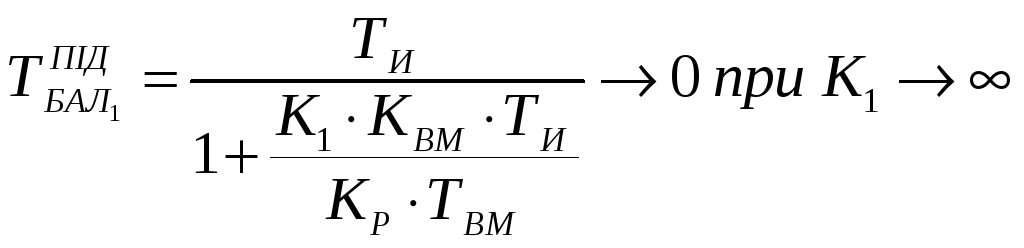
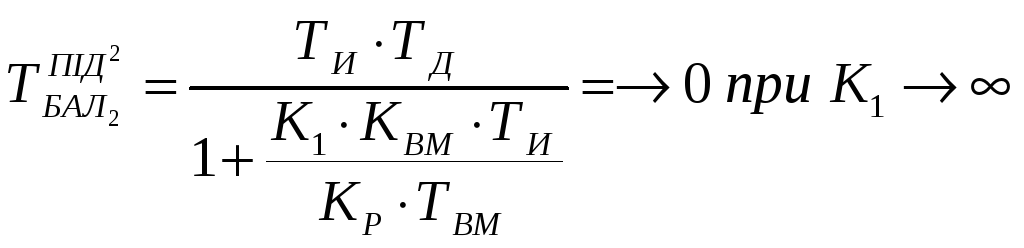 ,
вони наближаються до 0.
,
вони наближаються до 0.
![]()
Висновок: в ідеальній системі (граничній системі) в ідеальному регуляторі і ТБАЛ1 і ТБАЛ2 наближаються до 0, тобто баластна ланка в граничній системі – це пропорційна ланка з КР=1.
Чим якісніший операційний підсилювач(ОП), тим точніше формується ПІД-закон.
![]()
Т.ч. ТБАЛ1 і ТБАЛ2 пов’язані між собою через ТД, це означає, що як і в попередньому варіанті, граничне співвідношення параметрів ТИ і ТД буде:
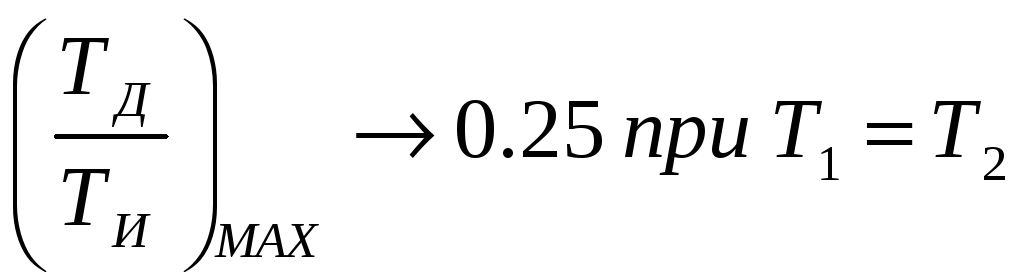 ,
,
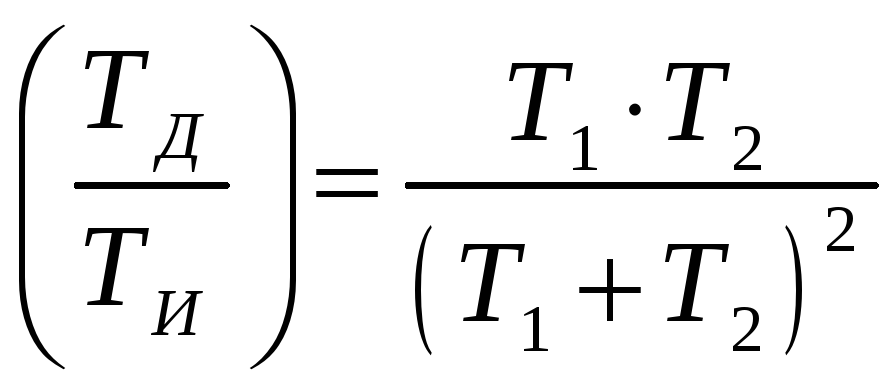
Висновок: D<0 – баластна ланка – інерційна ланка з коливальним затухаючим перехідним процесом.
Характеристичне рівняння перехідних процесів :
![]()
Якщо комплексні складові – нестійка, якщо уявні – коливальна, якщо дійсні – стійка.
![]()
