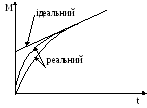§6. Реалізація лінійного пі-закону регулювання регулятором з вм постійної швидкості.

а) з охопленням зворотнім зв’язком ВМ сталої швидкості:

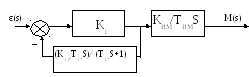
1 крок: визначимо тип ланки ЗЗ в ідеальному ПІ-регуляторі, для цього використаємо рівняння граничної системи:

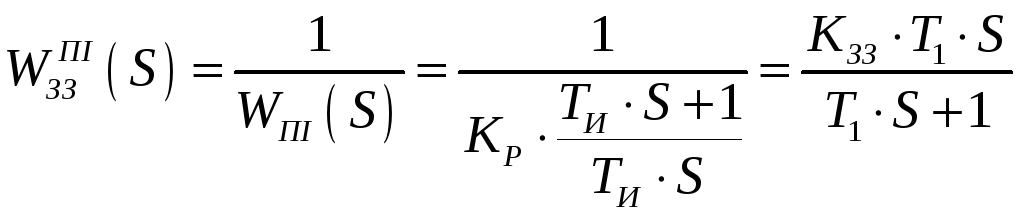
Т.ч. знаходимо, що зворотна ланка – це типова диференціальна реальна ланка. У ЗЗ для формування ПІ-закону потрібно встановити реальну диференційну ланку (із-за S в чисельнику і знаменнику).

2 крок: визначимо властивості такого реального регулятора, для чого запишемо еквівалентну передаточну функцію:

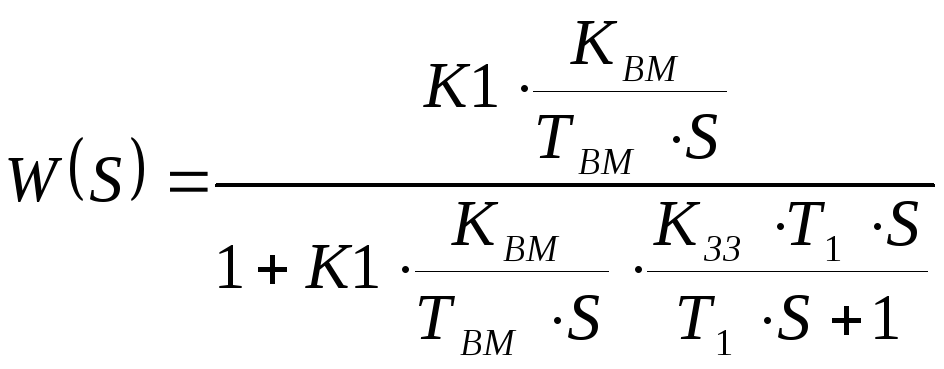
3 крок: відокремимо в останньому виразі ідеальний ПІ-регулятор і баластну ланку, помножимо чисельник і знаменник на :

,

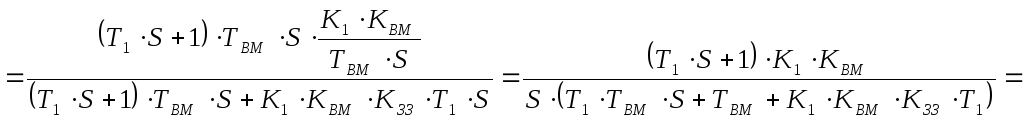
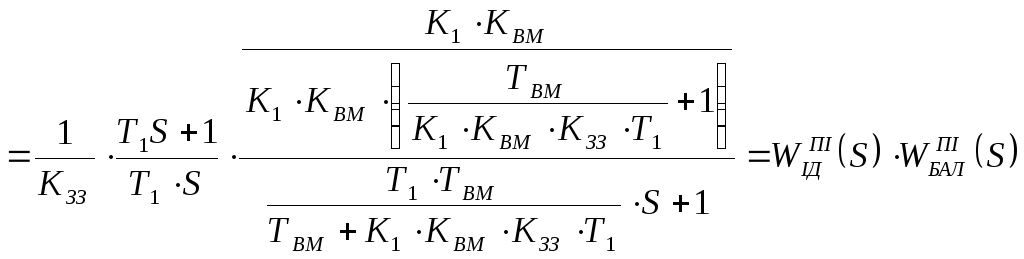Т. ч. реальний ПІ-регулятор можна представити, як послідовне з’єднання ідеального ПІ-регулятора і баластної ланки – аперіодичної ланки першого порядку, таким чином ідеальний закон може формуватися не точно.

4 крок: дослідимо властивості реального регулятора:

1). Оскільки передаточна функція ідеального ПІ-регулятора містить 2 параметри настройки К_Р і Т_И , то параметр постійної інтегрування (або час ізодрому) визначається постійною часу реальною диференційної ланки Т₁:

визначення параметрів настройки К_Р не залежить від Т_И.

2) властивості баластної ланки:

,

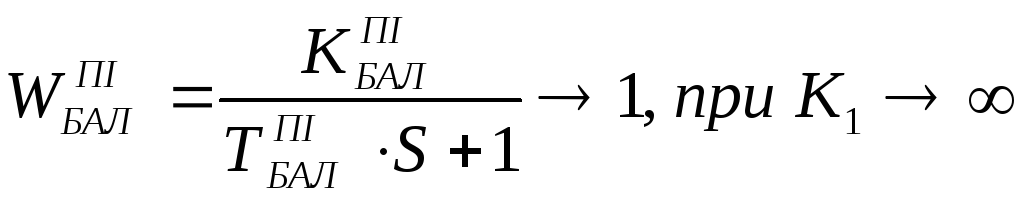Висновок: баластна ланка – це інерційна ланка першого порядку.

3) коефіцієнт передачі в граничній системі наближається до 1

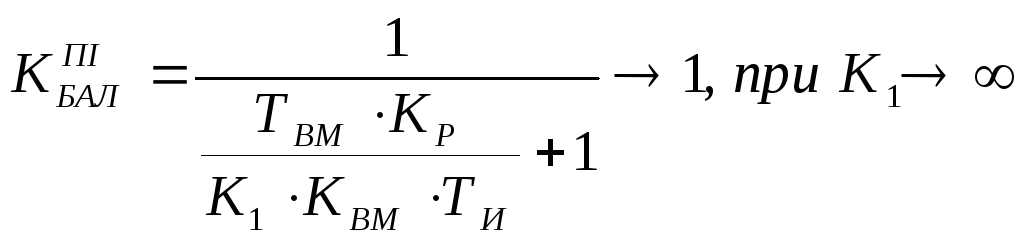. В реальному регулятори, де К₁ – якесь число,

- залежить від параметрів ВМ від якості операційного підсилювача і від параметрів автоматичного регулятора (АР):

4) постійна часу баластної ланки в граничній системі наближається до 0. приезжай

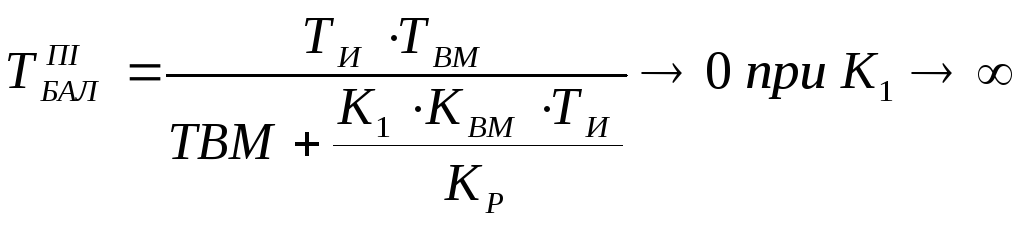, або інакше баластна ланка вироджується в пропорційну ланку з одиничним коефіцієнтом передачі.

5) в реальному регуляторі постійна часу залежить від всіх параметрів, що входять в формулу

Крива розгону ідеального і реального регуляторів:

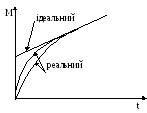
Поняття області нормальної роботи (ОНР).

Для реального автоматичного регулятора вводиться ОНР – це область у просторі стану АР (амплітуда і частота сигналу, що подається, і параметри настройки), в якій складові КЧХ реального регулятора відрізняються від КЧХ ідеального регулятора не більш на поперед задані величини.

∆

умови

М(ω)≤10% - модуль

∆Θ(ω)≤15град – фаза

Тому,

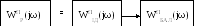
1) КЧХ ідеального П-регулятора:

Т. ч. на прикладі П-регулятора можна побачити, як визначається ОНР. Передаточна функція і КЧХ мають один і той же вираз. Точка 0≤ω≤∞ – це точка для будь-яких частот.

2) КЧХ баластної ланки реального П-регулятора – інерційна ланка:

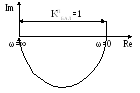Для інерційної ланки першого порядку КЧХ має вигляд напив кола з діаметром=1. При збільшені частоти сигналу, модуль КЧХ зменшується до 0. Значить, якщо ми за цими виразами побудуємо 3 графіки, то модулі перемножаться при нульовій частоті.

3. КЧХ реального П-регулятора:

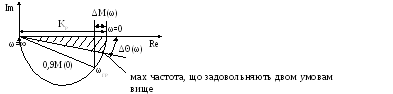
КЧХ реального регулятора має вигляд півкола з діаметром Кр, тобто промасштабовану КЧХ баластної ланки.

По цьому графіку можна визначити граничну частоту вхідного сигналу, що визначає ОНР регулятора.

ОНР – це заштрихована область на графіку.

ОНР для П-регулятора зображується, як :

ОНР для фіксованих граничних значень ω зображується у просторі настроєм.

Для ПІ-регулятора ОНР має вигляд :

Ці лінії мають різні значення Ти, тому область трохи деформується.

б) Реалізація ПІ закону регулювання без охоплення зворотнім зв’язком ВМ сталої швидкості:

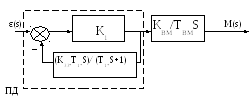
Визначимо передаточну функцію ланцюга ЗЗ.

Оскільки ВМ має властивості інтегральної ланки, а КПП включений послідовно з цим ВМ, то згідно з методом послідовної корекції, для одержання ПІ закону регулювання еквівалентною системою для формування П-складової , потрібно нейтралізувати інтеграл Д ланкою, а для формування інтегральної складової потрібно про масштабувати її П ланкою.

Т. ч. КПП повинен формувати ПД закон, виходячи з цього ми робимо 1 крок :

1 крок: визначимо передаточну функцію ланцюга ЗЗ.

В граничній системі закон регулювання визначається в ланці ЗЗ, т. ч. із рівняння граничній системи можна записати вираз :

.

2 крок: визначимо еквівалентну передаточну функцію структури для реального регулятора:

,

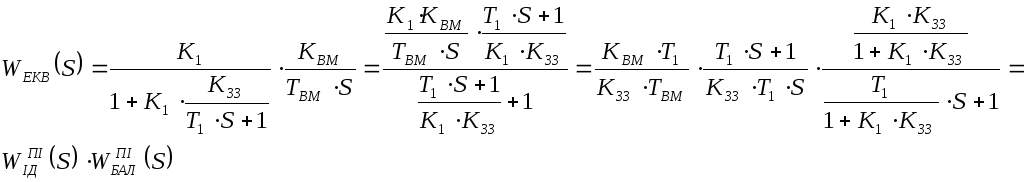
Властивості ПІ-регулятора:

Передаточна функція ідеального ПІ-регулятора:

1) , постійна часу інтегрування визначається постійною часу ЗЗ – Т_1.

Висновок: постійна часу інтегрування Т_И (ізодрому) повністю визначається величиною постійної часу ланки ЗЗ Т_1, як і в попередньому випадку, але К_Р записується, як:

, коефіцієнт передачі регулятора залежить від коефіцієнта передачі ланки ЗЗ К_ЗЗ, параметрів ВМ (К_ВМ і Т_ВМ) і параметрів настройки Т_И.

. Параметри настройки К_Р і Т_И взаємозв’язані.

2) В граничній системі передаточна функція баластної ланки наближається до 1, тому що Т_И наближається до 0:

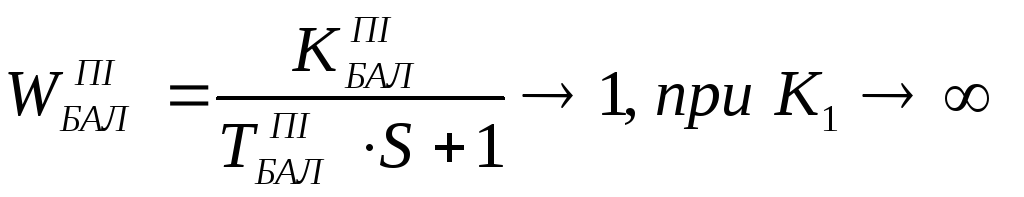, передаточна функція баластної ланки →1, тому, що

,

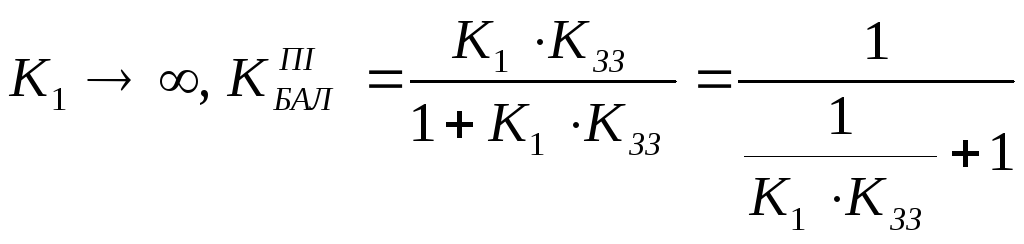Для реального регулятора вирази для :

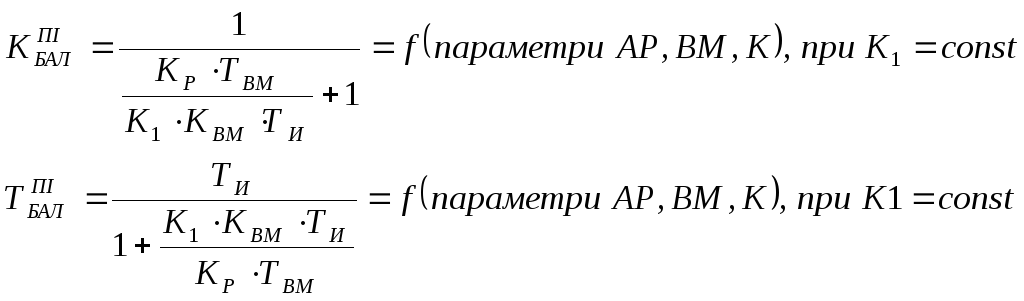
Крива розгону і ОНР аналогічні попереднім: