12. Математическая модель гидравлического демпфера.

Требуется построить структурную схему гидравлического

демпфера (амортизатора) с учетом массы подвижных частей. За

входную величину принята сила, а за выходную - перемещение

поршня (Рис.4.15).

где F - внешняя сила; г F - гидростатическая сила; и F - инерционная

сила; x - перемещение поршня; P1,P2 - давления в полостях

цилиндра; Q - расход жидкости через дроссель; S - площадь поршня;

Rг - гидравлическое сопротивление дросселя.

Здесь разность внешней силы F и внутренней гидростатической

силы Fг определяет инерционную силу Fи . Эта разность сил зависит

от разности давлений жидкости ∆P = P1 – P2 в нижней и в верхней

полостях цилиндра.

В свою очередь, инерционная сила Fи определяет ускорение

поршня x. Проинтегрировав ускорение x, получим скорость x , а

проинтегрировав скорость x , получим перемещение x . Скорость x определяет расход жидкости Q из нижней полости в верхнюю

полость, что при известном гидравлическом сопротивлении

дроссельного отверстия в поршне позволяет найти разность давлений

жидкости ∆P в нижней и в верхней полостях гидроцилиндра, а

следовательно, и гидростатическую силу Fг .

Сеть связей физических величин показывает рассмотренные

качественные зависимости физических величин (рис. 4.16).

Физические уравнения и соответствующие им передаточные

функции определяют количественные зависимости физических величин.

Структурная схема амортизатора

Структурная схема (рис.4.17) представляет собой

имитационную модель гидравлического амортизатора. Движение

этой модели легко описать с помощью системы линейных ДУ и

решить их с помощью ЭВМ.

13. Математическая модель двигатель пост. Тока.

Рассмотрим отдельно электрическую и механическую части

электрического двигателя.

Входной величиной здесь является напряжение, а выходной -

частота вращения вала двигателя w. Под влиянием напряжения, через

обмотку якоря протекает ток i, который, взаимодействуя с магнитным

полем возбуждения Ф, создает на валу электродвигателя движущий

момент (4.1)

где с - коэффициент, зависящий от конструкции двигателя.

При вращении якоря в магнитном поле в нем возникает ЭДС (4.2) Она направлена против питающего напряженияU и поэтому

вызывает уменьшение тока i. Коэффициент пропорциональности С в

формулах (4.1) и (4.2) зависит от конструкции двигателя и силы

магнитного поля Ф.

Рассмотрим схему замещения якорной цепи двигателя при

индуктивности якоря Lя =0 (рис.4.19). Внешнее напряжение U

уравновешивается суммой падения напряжения UR на омическом

сопротивлении R якоря U и ЭДС e.

Следовательно, можно записать:

Зная величину R U , можно определить ток i, а ток i определяет

момент M на валу двигателя, последний, в свою очередь, связан с

частотой вращения уравнением движения:

Определив w - найдем ЭДС е. Рассмотренную причинно-

следственную связь физических величин представим сетью связей

(рис.4.20).

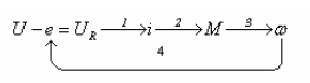
В соответствии с сетью связей, запишем физические

зависимости и следующие из них передаточные функции

Сопоставив полученные выражения для передаточных функций

с сетью связей, легко построить структурную схему двигателя

(рис.21).