17. Обобщённые алгоритмы имитационного моделирования. Алгоритм моделирования по принципу особых состояний.
В качестве событий выделены: -поступление заявки в систему; -освобождение элемента после обслуживания заявки; -завершения моделирования;(-возникновение отказа устройств; -завершение восстановления устройств-другие типы событий).
Процесс имитации
развивался с исп-ем управляющих посл-тей,
определяемых по функциям распр-я
вероятностей исх данных путём проведения
случ испытаний. В кач-е управляющих
посл-тей исп-лись в примере -ти значений
периодов следования заявок по каждому
i-ому потоку {
}
и длительности обслуживания заявок
i-ого потока устр-вом {
}.
Моменты наступления будущих событий
опр-лись по простым рекуррентным
соотношениям. Эта особ-ть даёт возм-ть
построить простой циклический алгоритм
моделир-я, кот сводится к след действиям:
1)опр-ся событие с мин-ым временем —
наиб раннее событие; 2)модельному времени
присваивается значение времени
наступления наиб раннего собы-тия;
3)опр-ся тип события; 4)в зав-ти от типа
события предпринимаются действия,
напр-ные на загрузку устр-тв и продвижение
заявок в соответствии с алгоритмом их
обработки, и выч-ся моменты наступления
будущих событий; эти действия наз-т
реакцией модели на события; 5)перечисленные
действия повт-ся до истечения времени
моделир-я. В процессе моделир-я произв-ся
измерение и стат обработка значений
вых-х харак-к. Обобщённая схема алгоритма
моделирования по принципу особых
состояний.
18. Обобщённые алгоритмы имитационного моделирования. Алгоритм моделирования по принципу t.
Укрупнённая схема моделирующего алгоритма, который реализует принцип постоянного приращения модельного времени (принципа дельта t)
В начале
инициализируется прога, в частности
вводятся значения
(
),
i=1,2,…k. Кот характ-т состояние системы
в k-мерном фазовом пр-ве состояний в нач
момент времени
.
Модельное время уст-ся t =
=
0. Осн операции по имитации системы
осуще-ся в цикле. Функционир-е системы
отслеживается по послед-ной схеме
состояний
(t).
Для этого модельному времени даётся
некот приращение dt. Затем по вектору
текущих состояний опр-ся новые состояния
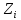(t
+ dt), кот становятся текущими. Для опр-я
новых состояний по текущим в формализованном
описании системы должны сущ-ть необх
мат завис-ти. По ходу имитации измеряются,
вычисляются, фиксируются необх выходные
хар-ки. При моделировании стохастических
систем вместо новых состояний выч-ся
распределения вероятностей для возможных
состояний. Конкретные значения вектора
текущих состояний опр-ся по рез-там
случайных испытаний. В рез-те проведения
имитац-го эксперимента получается одна
из возм-х реализаций случ-го многомерного
процесса в заданном интервале времени
(
,
).
Моделирующий алгоритм, основанный на применении dt применим для более широкого круга систем, чем алгоритм, построенный по принципу особых состояний. Однако при его реализации возникают проблемы опр-я величины dt. Для моделир-я ВС на системном уровне в основном исп-ся принцип особых состояний.