7. Классификация видов моделирования

Детерминированное – процесс, в котором предполагается отсутствие всяких случайных воздействий. Стохастическое – вероятностные процессы и события. Статическое – объект в какой-то момент времени. Динамическое – поведение объекта во времени. Мысленное – объекты, нереализуемые в заданном интервале времени, не поддающиеся физическому эксперименту. Наглядное - создаются наглядные модели. При гипотетическом закладывается некоторая гипотеза о закономерностях протекания процессов в реальном объекте. Аналоговое – основуется на применении аналогий различных уровней. Символическое – процесс создания логического объекта, замещающего реальный и выражающего основные его свойства с помощью знаков и символов. Математическое – процесс установления соответствия реальному объекту некоторого математического объекта. Аналитическое – процессы функционирования элементов системы в виде функциональных соотношений. Имитационное –модель, алгоритм которой воспроизводит процесс функционирования системы.

8. Универсальный способ получения случайных чисел

базируется на кусочной аппроксимации функции плотности. Пусть требуется получить последовательность случайных чисел {у_i} с функцией плотности f_n(y), возможные значения которой лежат в интервале (а, b). Разобьем интервал (а, b) на m интервалов. Тогда случайную величину  можно представить в виде , гдеak — абсцисса левой границы k-гo интервала; — случайная величина, возможные значения которой располагаются равномерно внутриk-го интервала.

Для вычисления ak воспользуемся следующим соотношением:

Алгоритм машинной реализации этого: 1) генерируется случайное равномерно распределенное число x_i из интервала (0, 1); 2) с помощью этого числа случайным образом выбирается интервал ; 3) генерируется числоx_i+1 и масштабируется с целью приведения его к интервалу , т. е. домножается на коэффициент; 4) вычисляется случайное число с требуемым законом распределения.

Достоинства способа: При реализации на ЭВМ требуется небольшое количество операций для получения каждого случайного числа, так как операция масштабирования выполняется только один раз перед моделированием.

9. Схема процесса моделирования

Модель объекта моделир-я – множ-во величин, опис. процесс функционир-я реальной системы и образующих подмножества входных воздействий на систему 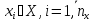, внутренних собств. параметров системы, выходные хар-ки системыи воздействие внеш. среды.и– непрересек. подмнож-ва, независ. переменные,– завис. переменные.

Математическая

модель

Процесс функционир-я системы S во времени описывается

–выходная траектория, совокупность зависимостей для всех.

As – алгоритм функионир-я – метод получ-я вых. хар-к с учетом и. Один и тот же законфунк-я системы може быть реализован различными алгоритмамиAs. Ф-ла явл. динамич. моделью системы. - статич. модель. Их соотношение получают через св-ва системы в конкр. моменты времени, наз. соответствиями.

Будем рассм. процесс функ-я системы как послед. смену состояний 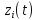, кот. могут быть интерпретированы как координаты точки вk-мерном пространстве: . Совокупность всех возможных значений состоянийназ-ся пространством состояний объекта моделир-яZ.