
- •1.Предмет, цели и задачи моделирования. Классификация и свойства моделей.
- •2.Этапы моделирования. Система и внешнее окружение. Методы создания моделей.
- •3.Основные понятия системного анализа. Типы систем управления. Построение моделей систем управления са.
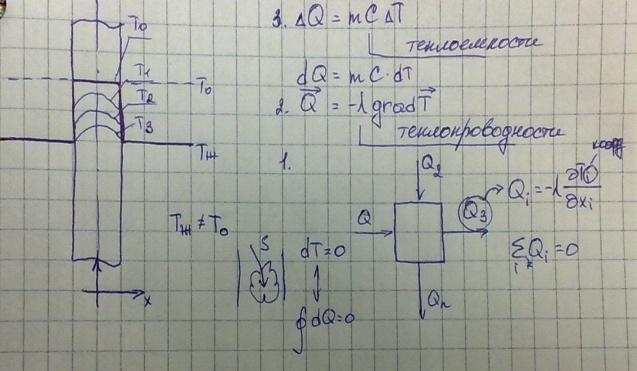
- •4.Модели на основе фундаментальных физических законов (на примере уравнения теплопроводности). Дискретизация и решение уравнений частных производных.
- •5.Регрессионный анализ и модели на основе регрессий.
- •8.Системы массового обслуживания. Цели, задачи и определение путем имитационного моделирования характеристик систем. Средства моделирования.
- •10.Планирование эксперимента. Полнофактроный и дробнофакторный эксперимент.
1.Предмет, цели и задачи моделирования. Классификация и свойства моделей.
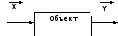
Эксперимент («натурный»): var (xi)yi
 ={x1,x2,…,xn}
={x1,x2,…,xn}
Недостатки:
Необходимость воздействия на объект
Не обладает повторяемостью
Высокая стоимость ($↑)
Продолжительные (∆ τ ↑)
Недостатки натурного эксперимента убрали и получили «вычислительный эксперимент», но не все.
Для вычислительного эксперимента необходимо наличие модели – это заменитель объекта для проведения с ним эксперимента.
Моделирование
- это исследование свойств объекта при
помощи эксперимента на модели.
Система – целостное подмножество элементов и связей между ними.
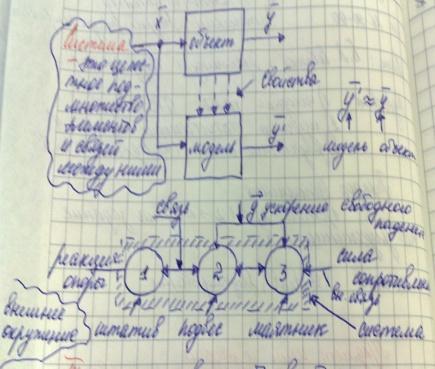
Топологией называется совокупность связей передающее взаимодействие между элементами системы.
Эмерджентность – это свойство системы отсутствующее у отдельных элементов.
Модели:
1. Натурная (реальная) – это замена одного
объекта другим
2. Знаковые - некоторое описание объекта
Вербальные (описательные) Пример: уголовный кодекс
3. Формализованные (Примеры: ноты)
аналитическая (получение конечной формулы)
-алгоритмическая
-(программная) – реализация алгоритмической на ЯП
-имитационная
Задачами моделирования являются:
Разделение системы и внешнего окружения
Формализация системы (ведет к построению аналитической модели)
- алгебраическая y=f(x)
-
обыкновенные дифференциальные уравнения

-
дифференциальные уравнения частных
производных
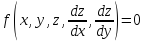
-
Интегральные дифференциальные уравнения

Принятие допущений, которые упрощают модель.
Оснащение модели – постановка уравнения состояния, const, свойств объекта
Задания граничных (дифференциальные уравнения частных производных) и начальных (дифференциальные уравнения) условий.
Метод решения
Переход к алгоритмической модели
Программная модель
Расчет по модели (получить y’)
Проверка адекватности (погрешности) – проводиться на основании тестового примера, который имеет легко получаемое аналитическое решение.
Если модель не адекватна, то происходит возврат 1-9.
Классификация моделей
Статической (независим от времени y=f(x)) и динамической (зависит от времени y=f(x,τ))
Непрерывные ({y,x}принадлежит R)и дискретные (каждая величина это набор каких-то возможных значений y=<y1,y2,..,yn> n не стремится к∞)
Детерминированные (y=(M[y],D[y]) при x1=3+/-1) и стохастические
Точечные (сосредоточенные y=f(τ) y:x принадлежит X) и распределенные (параметрическими y=f(x1,x2,τ) (x1,x2 принадлежит X))
Линейные (
 ),
нелинейные (y=exp(a*x))
),
нелинейные (y=exp(a*x))
Линеаризация
модели

2.Этапы моделирования. Система и внешнее окружение. Методы создания моделей.
Методы создания моделей
Функциональный метод – сводиться к решению обратной задачи моделирования
y=f(x)
«прямая» «обратная»
«идентификации»

<xi,yi>, i=1,N
xc{x1,x2,…,xn} регрессия
yc{y1,y2,…,yn} f(x):/y(xi)-yi/min
Структурный метод – построение иерархических моделей.
Принципы:
По уровню абстрагирования (параметры и характеристики важные на нижнем уровне перестают быть важными на верхнем).
Уровень сложности принимаемых решений
Уровень организационной структуры

Построение структурных моделей производятся методом системного анализа, который позволяет свести сложную задачу к последовательности решения простых задач.
