шпоргалка / 0450128_ADADE_shpargalki_k_ekzamenu_po_modelirovaniya_sistem
.docx
|
На практике часто ставят задачу найти коэффициенты модели заранее заданной структуры. Обычно берут ДУ первого порядка. В этом случае из кривой разгона предварительно выделяют транспортное запаздываение.
К – коэф. усиления. К находят по установившемуся значению. Для нахождения а1 находят точку перегиба. В этой точке вторая производная равна нулю.
|
Для определения а2 есть 2 подхода: *Рассматриваем кривую разгона при очень малых интервалах времени, когда первая производная равна 0 и ей можно пренебречь. *Интегрируем уравнение 2 порядка до точки перегиба. |
29.ОСНОВЫ ПАССИВНЫХ МЕТОДОВ ПОСТРОЕНИЯ МОДЕЛЕЙ СТАТИКИ Данные методы не предполагают активного воздействия на процесс с целью определения влияния входных величин, используется наблюдение за нормальным ходом процесса. При естественном ходе есть колебания входных и выходных переменных. В результате обработки длительных интервалов наблюдений можно получить статическую или динамическую модель. Статическую модель получают через коэффициент корреляции.
|
|
r- коэффициент линейной корреляции. Основная проблема состоит в трудности получения статических режимов. Для построения моделей динамики в основном использ-ся методы спектрального анализа. Для этого вычисл-ся характеристики входного и выходного случайного сигнала. При вычислении получ-ся в виде какого-то графика и их надо аппроксимировать подходящим выражением. Если спектральные характ-ки показывают наличие спектральных составляющих, то это не мешает получение математич-й модели. В ряде случаев удобно использ-ть взаимные спектральные характ-ки, что лучше сделать взаимной корреляционной функцией. Построение динамич. Моделей пассивынми методами осложнено трудностями: |
1. оказывает автокореляционная функция. Надо убедиться, что коэффиц-т автокорел-и близок к нулю. 2.Эти методы работают для оргодических функций. 3. Существенное влияние оказывает временная дискретизация случайных процессов. 4. Плохо формализуем, поэтому надёжность пассивных методов невысокая, хотя когда случ. Процесс существенен, то такие эффективны. 5. Требуется достаточно большое число экспериментальных данных, как минимум несколько сотен. 30.АНАЛИТИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ. ЭТАПЫ ПОСТРОЕНИЯ МОДЕЛИ. При построении модели химико-технологического процесса используются в качестве основополагающих балансовые соотношения: балансы расходов, балансы энергии, количества движения и другие. |
Необходимо иметь ввиду, что в объекте возможно накопление вещества, зарядов, энергии, а также возможно существование внутренних источников энергии. Основные допущения определяются условиями работы объекта и их справедливость должна обосновываться, иначе модель будет неадекватной. Допущения можно объединить: 1) Допущения о постоянстве или об известном законе изменения физических свойств участвующих в процессе объектов. Хотя свойства и зависят от большого числа факторов, но если диапазон их изменения в области применения модели невелик (5-10%), тогда их принимаем постоянными. Если модель будет применяться в широком диапазоне изменения режимов, тогда принятие допущения необходимо обосновать. |
|
2) Допущения о неизменном или известном характере изменения геометрических размеров аппарата. Необходимо помнить о форме аппарата, если одни параметры зависят от других (например зависимость площади сечения в коническом аппарате от высоты). В случае проектирования новых процессов или аппаратов требуется получить оптимальные зависимости от требуемых условий, но это уже задача оптимизации она вариационная и решается достаточно сложно. 3) Допущения о характере потоков веществ и энергий. Поток вещества – распределение какого-либо параметра в пространстве. Чаще всего имеет место реальная распределенность параметров процесса в пространстве по сечению аппарата. Принятие допущений о постоянстве параметров существенно упрощает модель, т.е. можно |
обычных производных или обычным ДУ. Только необходимо учесть влияние распределения параметров на конечный результат моделирования. 4) Допущения о значимости отдельных явлений и о необходимости их учёта в модели. Это самый сложный и субъективный вид допущений. Часто все элементарные процессы не известны или не изучены, тогда опираемся на свой опыт или опыт других исследователей.. Часто сознательно пренебрегаем многими явлениями или описываем дискретные процессы будто они имеют непрерывную структуру – потоки жидкостей, эмульсии и т.д. 5)Допущения о потерях вещества и энергии. Потери, особенно тепловые присутствуют всегда, т.е. об их отсутствии говорить нельзя, а только можно говорить о малости их изменения при смене режимов работы объекта. Однозначных рекомендаций на этот счёт нет, т.к. задач много и исследователи разные:) |
В общем случае модель химико-технологического процесса может включать в себя следующие данные: - модели потоков - модели массообмена - модели хим реакций - модели тепловых эффектов - связующие уравнения Порядок построения модели 1) Анализируем объект и определяем задачу моделирования, выбираем входные и выходные переменные и каналы, по которым будем строить модель. 2) Принимаем основные допущения. Во время построения модели допущения могут дополняться. 3) Записываем балансовые соотношения для статики (балансы веществ, энергии, количества движения и др) 4) Рассматриваем приращение входных воздействий по выбранным каналам |
|
5)Записываем модель динамики в приращениях с учётом накопления вещества и энергии 6) Переходим к пределу при Δt->0 6+) При достаточном опыте можно сразу записать ДУ вместо 5 и 6 с учётом формулировки: «Скорость изменения вещества или энергии пропорциональна разности притока и утока вещества или энергии». 7) Раскрываем соотношения между переменными в объекте 8) Если необходимо, то линеаризуем 9) При необходимости производим нормировку переменных, т.е. приводим к безразмерному виду с учётом технологических требований. 10) Если выполнены 8 и 9, то при возможности преобразуем по Лапласу и получаем передаточную функцию |
28.ПРИБЛИЖЕННЫЕ МЕТОДЫ ПОСТРОЕНИЯ МОДЕЛЕЙ ДИНАМИКИ Записываем соотв. ДУ
Прямыми методами подбираются коэф. Следует помнить, что при поборе а модет меняться структура решения, т.е. хвых расчетная. В . хвых расч. Коэф. а входят не долько как сомножители, но и в показатели степени. R(а) будет овражной, что существенно усложняет поиск минимумов. |
Задачу поиска модно несколько упростить если в качестве меры близости использовать не близость между расчетными и экспериментальными значениями, а близость между правой и левой частями уравнения.
Такой подход сравнительно легко применяется при построении модели 2 порядка и рассматривают близость в отдельный момент времени.
|
|
На практике часто ставят задачу найти коэффициенты модели заранее заданной структуры. Обычно берут ДУ первого порядка. В этом случае из кривой разгона предварительно выделяют транспортное запаздываение.
К – коэф. усиления. К – коэф. усиления. К находят по установившемуся значению. Для нахождения а1 находят точку перегиба. В этой точке вторая производная равна нулю. |
Для определения а2 есть 2 подхода: *Рассматриваем кривую разгона при очень малых интервалах времени, когда первая производная равна 0 и ей можно пренебречь. *Интегрируем уравнение 2 порядка до точки перегиба. |
31.ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ НАПОРНОГО БАКА Порядок построения модели 1) Анализируем объект и определяем задачу моделирования, выбираем входные и выходные переменные и каналы, по которым будем строить модель. 2) Принимаем основные допущения. Во время построения модели допущения могут дополняться. 3) Записываем балансовые соотношения для статики (балансы веществ, энергии, количества движения и др) 4) Рассматриваем приращение входных воздействий по выбранным каналам |
|
5)Записываем модель динамики в приращениях с учётом накопления вещества и энергии 6) Переходим к пределу при Δt->0 7) Раскрываем соотношения между переменными в объекте 8) Если необходимо, то линеаризуем 9) При необходимости производим нормировку переменных, т.е. приводим к безразмерному виду с учётом технологических требований. 10) Если выполнены 8 и 9, то при возможности преобразуем по Лапласу и получаем передаточную функцию
|
1) Входная величина – расход жидкости, выходная - уровень 2) Допущения: плотность, температура и сечение бака постоянны
|
Материальный баланс в приращениях в динамике. Приток не равен стоку и разница пойдет на накопление.
|
|
|
|
|
|
Данное разложение в ряд справедливо, когда не меняется фазовое состояние потока. В случае ограничения в ряде только линейными членами:
В итоге получаем обычный апериодический объект:
|
Если сток из резервуара осуществляется не под давлением столба жидкости, а под действием насоса постоянной производительности, то свойства объекта радикально изменяются. 32.ПРОСТЕЙШАЯ МОДЕЛЬ НАГРЕВА ТЕЛА
|
Рассматриваем нагрев твердого тела в потоке, т.е. общий случай теплообмена тела со средой. Допущения: 1)Имеет место конвективный теплообмен с граничными условиями 3 рода, т.е. когда количество тепла пропорционально разности температур и площади поверхности.
)Линейный закон теплообмена с постоянным α 3)Подвод тепла осуществляем с очень высокой скоростью, т.е. большое α и температура самого потока меняется несущественно. 4)Теплофизические характеристики объекта изменяются несущественно с изменением температуры, поэтому считаем их постоянными
|
|
Все тепло тратится на нагрев тела:
Делим Δq на Δt и берем предел при Δt->0
33.МОДЕЛЬ СМЕСИТЕЛЯ
|
Входными воздействиями могут быть входные расходы и входные температуры. Принимаем допущения о небольшой разнице входных и выходных температур и о несущественном изменении свойств. Эти допущения можно обосновать сопутствующими технологическими процессами, посему считаем плотности и теплоёмкости потоков постоянными. При построении модели данного объекта придётся учитывать материальные и тепловые балансы, т.к. возможно накопление вещества и энергии. Материальный баланс в статике:
Тепловой баланс в статике:
К-коэффиц-т теплопередачи |
Отсюда находим Т30 Запишем теплвоой баланс в приращениях, для простоты расм. только два входа, напр, Т1 и Q2:
Будет считать, что в аппарате имеется эффективное перемешивание и темпер-ра в аппарате равна во всех точках по обмену и след-но равна темпер-ре воды на выходе: Тап=Т3 Раскрываем скобки. Приращения ∆q и ∆t явл-ся малыми, поэтому произвед-е 2-х малых явл-ся величиной 2-го порядка малости и можно пренебречь.
|
|
Коэф-т при первой производной по темпер-ре явл-ся переменной величиной, т.е. модель явл-ся нелинейной. В частноти это может привести к след. последствиям. При создании системы автоматич-го регулирования по темпер-ре, настроечные параметры регул-ра зависят от коэф-та при производной. Поэтому при регулировании темпер-ры в случае малого уровня настройки регул-ра должны быть одни, а при регулировании темпер-ры при большом уровне, настройки другие. Получ-ся должна быть аддитивная система регулирования подстраивающаяся под уровень. |
Т.о. модель будет представлять систему уравнений, причём входные потоки Q1 и Q2 влияют как на материальный так и тепловой баланс. (темпер-ры не влияют) На практике в подобных системах применяется 2 контура регулирования по температуре и по уровню разными потоками. Если уровень в аппарате по технологии может изменяться в широких пределах, то разделение систем невозможно. 34.МОДЕЛЬ ГАЗОВОГО РЕСИВЕРА (АППАРАТА С ГАЗОМ ПОД ДАВЛЕНИЕМ)
|
Газовые потоки при изменении давления меняют свою плотность, поэтому рассматриваем не объёмные, а массовые расходы потоков газа. Материальный баланс:
Уравнение балансов в динамике имеют вид:
Если изменяется расход на притоке или на стоке, то в аппарате будет происходить накопление газа:
|
|
Накопление массы приведет к изменению давления. Для связи используем уравнение Менделеева- Клайперона:
Принимаем дополнительное допущение о том что газ идеальный, объём аппарата постоянен, расширение и сжатие газа происходит достаточно медленно, аппарат имеет высокий коэффициент теплоотдачи с окружающей средой следовательно изменением температуры газа пренебрегаем.
|
Получили апериодическое звено 1 порядка.
35.МОДЕЛЬ ПЕРЕМЕЩЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ P1> P1
Q1 Q2 ξ ρ ρ Условно всё гидравлическое сопротивление линии сосредоточено в регулирующем органе, хотя сама труба вызывает гидравлические сопротивления, изгибы. В данном случае балансовым соотношением явл-ся баланс количества движения, получим такую модель при допущении: |
Q1= Q2 Рассм. вывод такого уравнения при допущении, что трубопровод заполнен: изменение количества движения равняется разности сил
Движение происходит гориз-но, силы тяжести не оказывают влияния.
|
|
Сопротивление в регулирующем органе влияет на расход через изменение скорости, сущ-т 3 течения режима: 1. очень маленькие скорости
2. очень большие скорости
3. скорость обратно пропорциональна сопротивлению
|
Линейный апериодический объект 1-го порядка. После линеаризации можно привести к типовому апериодическому звену, у которого будет маленькая постоянная времени, т.е. этот объект по каналу ξ-Q малоинерционный. Это накладывает отпечаток на управление расходом, на системы стабилизации расхода. Системы должны быть высокого быстродействия. Поэтому нередко лучшим регулир-м бывает П-регулятор, если не предъявляется особых требований к статической ошибке.
|
36.МОДЕЛИ ГИДРОДИНАМИКИ ПОТОКОВ. ОБЩИЕ СВОЙСТВА И ОСОБЕННОСТИ Поток – движение любой субстанции, жидкости, газа, энергии, температуры, концентрации. Большинство технологических процессов осуществляется в потоке, поэтому характер потока определяет процесс и он должен быть учтён при построении модели. Рассмотрим движение жидкости в потоке. Каждая частица имеет конвективную (вдоль потока) и диффузионную (поперёк потока) составляющие, т.е. в общем случае она движется в произвольном направлении.
|
|
Диффузионная составляющая определяется диффузией одного вещества в другом за счёт диффузии молекул, описываемых законом Фика:
cV - плотность потока [кг/м2с] I=I1+I2 – потоки вещества Надо знать характер потока для того, чтобы понять тот путь, который проходит частица в процессе. Диффузионная составляющая описывается соответствующими законами деффузии I=-Dgradc Закон теплопроводности Е=-λgradT |
Если движение потока ламинарное, то в нем нет равномерного распределения скорости. При ламинарном движении отсутствует диффузионная составляющая как для частицы жидкости. Для учёта пристеночных явлений – неравномерного распределения скоростей возможно ввести фиктивную диффузионную составляющую Для турбулентных потоков нередко вводят дополнительный коэффициент турбулентности с помощью которого можно учесть неравномерность потока:
Существует несколько подходов к описанию потоков: |
- аналитический - экспериментальный - использование типовых моделей потоков Аналитический Основан не теоретическом анализе характера потока в аппарате – очень сложен. Необходим учёт конфигурации аппарата, режимов течения, внешних воздействий и т.д. Применяется при проектировании процессов на стадии создания. Экспериментальный Тоже достаточно сложен, т.к. необходимы сложные эксперименты: а) измеряют в различных точках реальную скорость изменения параметров. При этом нужно не нарушать имеющиеся скорости средством измерения. б) оценка потока с помощью трассёров. |
|
Трассер (импульсно добавляемое в поток вещество, не взаимодействующее с веществом потока и не влияющее на технологический процесс, его концентрацию легко измерить), на основании анализа концентрации его в выходном потоке строятся кривые вымывания. Они показывают какое время та или иная доля частиц пребывала в аппарате. По полученному графику и определяют параметры моделей. Модельный Существует ряд простейших типовых моделей, путём комбинации которых возможно составить модель любой сложности. - модель идеального перемешивания - модель идеального вытеснения - ячеечная модель |
- диффузионная модель 37. ТИПОВЫЕ МОДЕЛИ ГИДРОДИНАМИКИ. МОДЕЛЬ ИДЕАЛЬНОГО ПЕРЕМЕШИВАНИЯ. Существует набор типовых моделей гидродинамики, с помощью которого возможно описать любой сложный технологический процесс: - модель идеального перемешивания - модель идеального вытеснения - ячеечная модель - диффузионная модель Модель идеального перемешивания
|
Рассм. в качестве входного потока раствор вещества раствор вещ-ва А в воде. Допущение: В общем случае концентрация на входе невелика и меняется не очень существенно, поэтому ρ=const.
|
|
Температ-ру будем считать потсоянной и потока и окр. среды. В данном случае можель будет включать в себя два материальных баланса: -
общий
-
покомпонентный Исходя из общего уравнения материального баланса возможно получить изменение уровня при изменении входного расхода или изменении сопротивления регулирующих органов. Рассмотрим изменение концентрации в аппарате при изменении входной концентрации.
|
При этом общий материальный баланс не изменится, а изменится только для компонента А. Для записи по комп. А в динамике примем допущение, что конвективной составляющей изменения концентрации можно пренебречь, а учитывать только диффузионную. Это главное и основное допущение модели идеального перемешивания. Следствием этого допущения явл-ся равенство по объему концентрации и след-но концентрация на выходе равна концентрации в аппарате. Для иллюстрации этого допущения в аппаратах изображают мешалку.
|
Изменение концентрации потока вещества на входе приведёт к накоплению вещ-ва А в аппарате и след. к измене-ю его концентрации. Если изменяется входная концентрация, то в аппарате будет накапливаться вещество:
Получается апериодическое звено 1 порядка, где V/Q – время пребывания вещества в аппарате. Такие аппараты примен-ся для пассивного сглаживания пульсации. Чем больше ёмкость, тем эффективнее. |
|
38.ТИПОВЫЕ МОДЕЛИ ГИДРОДИНАМИКИ. МОДЕЛЬ ИДЕАЛЬНОГО ВЫТЕСНЕНИЯ Существует набор типовых моделей гидродинамики, с помощью которого возможно описать любой сложный технологический процесс: - модель идеального перемешивания - модель идеального вытеснения - ячеечная модель - диффузионная модель Модель идеального вытеснения Модель основана на поршневом представлении движения жидкости, т.е. скорость движения частиц в любой точке сечения одинакова, т.е. в модели присутствует только конвективная составляющая. |
В статике и в динамике расходы равны, т.к. накопление энергии или массы невозможно. Изменение концентрации описывается:
Рассмотрим концентрацию в приращениях, т.е. при нулевых начальных условиях. Входное воздействие – изменение концентрации на входе. |
Если х=0, то k=C(0,р).
|
|
Таким образом получили звено чистого транспортного запаздывания. |
39.ТИПОВЫЕ МОДЕЛИ ГИДРОДИНАМИКИ. ЯЧЕЕЧНАЯ МОДЕЛЬ Существует набор типовых моделей гидродинамики, с помощью которого возможно описать любой сложный технологический процесс: - модель идеального перемешивания - модель идеального вытеснения - ячеечная модель - диффузионная модель Ячеечная модель |
представляется в виде последовательного соединения одинаковых объектов идеального перемешивания и только их! Передаточная
функция объекта:
Особенностью является то, что необходимо производить подбор 2 параметров T, n <=5. Данная модель занимает промежуточное положение между моделями идеального смешения(n→∞) и идеального перемешивания(n=1). Есть несколько модификаций ячеечной модели: *модель с обратными потоками Если все потоки есть и все к различны, то передаточная функция будет иметь вид: |
|
При большом числе зон получим модель идеального вытеснения, а при 1 зоне модель идеального перемешивания. В оригинальных моделях можно учитывать: - наличие застойных и «мертвых» зон - байпасные потоки - рециркуляция Застойной зоной назыв. такие участки аппарата, в кот-х время пребывания вещ-ва более чем в 3 раза отличается от среднего времени пребывания. Соответств-но выделяют застойные |
зоны с определённой кратностью обмена, т.е. с определён. долей потока, кот-я с единицей времени потока уходит. Могут существ-ть мёртвые застойные зоны, в кот-х вообще никогда не меняется вещество. 40.ДИФФУЗИОННЫЕ МОДЕЛИ Эти потоки предназначены для учёта диффузионных потоков в различных направлениях пространства. Есть три модели: Однопараметрические модели Данная модель учитывает конвективную и диффузионную составляющие и описывает распределение по 1 координате:
|
D-коэф-т диффузии, который в общем случае позволяет описывать источники разной природы, напр, в чистом виде молекулярная диффузия, турбулентность потока. Двухпараметрическая модель Учитывает распределение по 2 координатам, например по длине и по высоте сечения, например процесс осаждения в потоке:
Такая модель предназначена для описания распределения параметра потока, напр, в направлении перпендикулярном оси движения потока Трехпараметрическая модель
|






 Такой
алгоритм применяется чаще, потому что
определить экспер. значения производных
по кривой разгона сравнительно не
сложно. Наиболее хорошим методом для
этого является сплайновая аппроксимация
и интерполяция.
Такой
алгоритм применяется чаще, потому что
определить экспер. значения производных
по кривой разгона сравнительно не
сложно. Наиболее хорошим методом для
этого является сплайновая аппроксимация
и интерполяция.



 потерь вещества
нет
потерь вещества
нет


 ;
;
 ;
;

























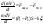






 Т.о. с помощью
введения конвективной диффузионной
составляющей возможно учесть различную
природу непостоянства по сечению
скорости потока.
Т.о. с помощью
введения конвективной диффузионной
составляющей возможно учесть различную
природу непостоянства по сечению
скорости потока.