Дискретно - детерминированные модели (f-схемы).

Дискретно - детерминированные модели в своей основе содержат теорию автоматов. На основе этой теории система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свое внутреннее состояние лишь в допустимые моменты времени. Автомат можно представить в виде черного ящика, на который подаются входные воздействия и снимаются выходные и который может иметь множество внутренних состояний.

Автомат, у которого множество входных переменных и множество внутренних состояний, а следовательно и множество выходных состояний конечно называется конечным автоматом.

Автомат F можно описать множеством входных, выходных, внутренних состояний, начальным значением z₀, функцией переходов  и функцией выходов : F = < X, Y, Z, z₀, ,  >.

Функция перехода  определяет состояние z’, в которое перейдёт система, если она находилась в состоянии Z и на ее вход поступило входное воздействие X. z' = (z, x) ;

Функция выхода  определяет выходное значение Y, которое принимает система, если она находилась в состоянии Z и на ее вход поступил сигнал X: y = (z, x).

Для задания автомата используется табличный или графический способ. При табличном способе в строках записываются входные воздействия автомата X, а в столбцах – состояния Z. На пересечении i-той строки и j-того столбца ставится значение функции перехода.

Так для системы, которая может находиться в трех различных состояниях и содержащей 3 входа F-автомат можно задать следующим образом:

Таблица переходов:

x\z	z0 = 0	z1 = 1	z2 =2	z3 =3
x1	1	2	3	0
x2	2	3	0	0
x3	3	0	0	0

Таблица выходов

x\z	z0 = 0	z1 = 1	z2 =2	z3 =3
x1	0	0	0	1
x2	0	0	1	1
x3	0	1	1	1

При графической форме записи каждому состоянию соответствует отдельная вершина. Каждому переходу соответствует дуга, вес которой совпадает со значением входного сигнала. В скобках ставится значение выходного сигнала.

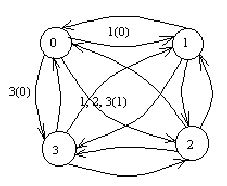
Дискретно-стохастические модели ( р-схемы)

Дискретно-стохастические модели рассматриваются на основе вероятностных автоматов. Вероятностный автомат – это дискретный потактовый преобразователь информации с памятью, функционирование которого обусловлено лишь состоянием памяти в такте и может быть описано в нем статистически. Пусть задано некоторое множество G пар вида (x_i, z_к), где x_i – элементы входного множества X, z_к – элементы множества состояний системы Z. Пусть задано некоторые множество F пар вида (z_к, y_j), где y_j – элементы выходного подмножества Y. Пусть любые элементы множества G индуцируют на множестве F некоторый закон распределения:

Элементы из F (z₁, y₁),(z₁, y₂),...(z₁, y_J),... (z_к, y_J-1), (z_к, y_J) (1)

Элементы из G b₁₁ b₁₂ b_1J b_KJ-1 b_KJ

,

где b_кj– вероятность перехода автомата в состояние z_к и появления на его выходе сигнала y_J, если он был в состоянии z_s и на его вход поступил сигнал x_i.

Если множество таблиц типа (1) обозначить через В, то вероятностный автомат можно описать в виде четырех множеств < X, Y, Z, B >.

Если выходной сигнал Р_авт определяется детерминированно, то такой автомат называется Y-детерминированным автоматом.

Если выбор нового состояния является детерминированным, то такой автомат называется z-детерминированным.

Способы задания вероятностных автоматов.

1. С помощью таблиц

Рассмотрим Y-детерминированный автомат. В столбцы и строки записываются состояния автомата. На пересечении i-ой строки и j-го столбца в таблице переходов – вероятность перехода автомата из состояния z_i в состояние z_j. В j-м столбце таблицы выходов – значение выходной функции при условии, что автомат находился в состоянии z_j.

Таблица переходов:

Zк	z1	z2	...	zK
z1	p11	p12	...	p1к
z2	р21	р22	...	p2к
...	...	...	...	...
zK	рк1	рк2	...	рКК

Таблица выходов:

Z	z1	z2	z3	...	zк
Y	yi1	yi2	yi3	...	yiк