
- •1.Моделирование как метод научного познания. Понятие модели. Классификация моделей. Цели и задачи моделирования. [1/1]
- •2. Требования к математической модели. Основные этапы построения модели. Иерархия моделей. [1/1]
- •3. Построения общесистемной модели функционирования. [1/2]
- •4. Основные системные свойства: линейность, непрерывность, стационарность, детерминированность. Классификация математических моделей. Системные и конструктивные модели. [1/2]
- •5. Непрерывно-детерминированные модели (d-схемы). Уравнения вход-выход. Уравнения в пространстве состояний. [1/3]
- •6. Разностные уравнения. Пример построения конструктивной и машинной модели системы. [1/1]
- •7. Дискретно – детерминированные модели (f- схемы). Автоматы Милли и Мура. Разновидности детерминированных автоматов. [1/2]
- •8. Дискретно стохастические модели. (p- схемы). [1/1]
- •9. Z – детерминированные и y – детерминированные вероятностные автоматы. [1/2]
- •10. Марковские случайные процессы. Простейший поток отказов. [1/1]
- •11. Уравнения Колмогорова для определения вероятностей состояний системы. Пример. [1/3]
- •12. Непрерывно-стохастические модели (q-схемы). Основные понятия и определения. [1/3]
- •13. Обобщенные модели (а - схемы). Понятие агрегата. [1/1]
- •14. Структура агрегативной системы. Особенности функционирования. [1/3]
- •15. Построение и реализация моделирующего алгоритмов
- •16. Построение детерминированного и циклического моделирующего алгоритмов q-схем. [1/1]
- •17. Построение циклического моделирующего алгоритма
- •18. Построение синхронного моделирующего алгоритма
- •19. Построение спорадического моделирующего алгоритма
- •20.Цели и задачи имитационного моделирования. Имитационная модель, имитационная система. Архитектура имитационной системы. [1/2]
- •21. Общая характеристика метода статического моделирования. Пример построения моделирующего алгоритма. [1/2]
- •23. Метод получения псевдослучайных чисел с равномерным законом распределения. Методы середины квадрата и середины произведения. [1/1]
- •24. Конгруэнтные процедуры генерации псч. Мультипликативный и смешанный методы. [1/1]
- •25. Тесты проверки случайности последовательности псч с равномерным законом распределения. [1/1]
- •26. Тест проверки равномерности закона распределения.[1/1]
- •27. Тест проверки независимости последовательности псч[1/1]
- •28. Моделирование случайных событий. [1/2]
- •29. Моделирование Марковских цепей. [1/1]
- •30. Моделирование дискретных и непрерывных случайных величин с заданным законом распределения. [1/2]
- •31. Приближенные способы преобразования случайных чисел. [1/2]
- •32. Моделирование непрерывных случайных векторов. [1/1]
- •33. Моделирование дискретных случайных векторов
- •34. Сети Петри (n - схемы). [1/2]
- •35.Языки моделирования. Типовая схема архитектуры языка имитационного моделирования. Способы управления временем в модели системы. [1/2]
- •36.Сравнительный анализ языков имитационного моделирования. [1/2]
- •40. Моделирование процессов функционирования систем на базе n-схем. Структурный подход. [1/2]
6. Разностные уравнения. Пример построения конструктивной и машинной модели системы. [1/1]

В
уравнениях (1) заменим![]() на выражение :
на выражение :
![]()

Разностные уравнения описывают поведение системы в дискретном времени t=0, h, 2h,…
Процесс вычисления по методу Эйлера сводиться к следующему :
x(0),
z(0)
![]() z(h),
y(h)
z(h),
y(h)
x(h)
![]() z(2h),
y(2h)
и т.д.
z(2h),
y(2h)
и т.д.
Существует h(h<<1) погрешность вычислений близка к h2 на каждом шаге
Пример:
![]()

Требуется: записать уравнение в нормальной форме Коши. Пользуясь методом Эйлера перейти к разностным уравнениям : z1=x; z2=x’; z3=x”;
![]() 1=z2;
1=z2;
![]() 2=z3;
2=z3;
![]() 3=
-a3*
z1-a2*
z2-a1*
z3+b0*u
3=
-a3*
z1-a2*
z2-a1*
z3+b0*u
![]() ;
;
![]() ;
;![]()
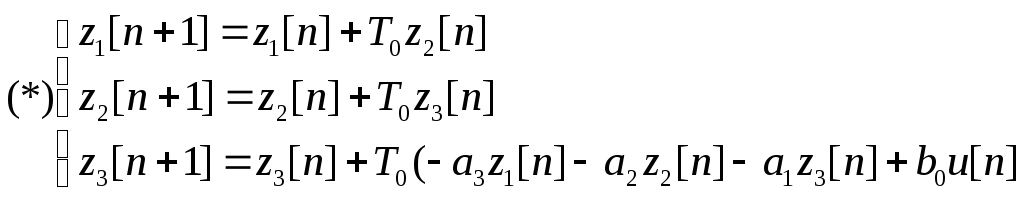
n=1, 2, 3,…
(*) – разностные уравнения.
10
7. Дискретно – детерминированные модели (f- схемы). Автоматы Милли и Мура. Разновидности детерминированных автоматов. [1/2]
В общесистемной модели интервал
функционирования является дискретным,
т.е.t=nh,
где n=
0,1,2.. . X,
Z
,Y
– являются конечными, т.е. содержат
конечное число элементов.
общесистемной модели интервал
функционирования является дискретным,
т.е.t=nh,
где n=
0,1,2.. . X,
Z
,Y
– являются конечными, т.е. содержат
конечное число элементов.
h – шаг дискретизации.
Конечный
автомат
представляет собой объект, который
функционирует в моменты автоматного
времени t0=0,
t1=h,
t2=2h
и т.д. Причем в каждый момент ti
![]() T,
автомат может находиться в одном из
конечного числа состояний zj
T,
автомат может находиться в одном из
конечного числа состояний zj![]() Z.
Z.
В
ответ на поступление входного сигнала
xj
![]() X,
автомат реагирует следующим образом:
X,
автомат реагирует следующим образом:
1) Его составляющие изменяются в соответствии с его функцией состояния
![]() ,т.е.
z(t+h)=
,т.е.
z(t+h)=![]() [z(t),x(t)]
[z(t),x(t)]
2) в каждый момент автоматного времени на выходе появляется сигнал
y(t)
![]() Y,
который определяется функцией выходов
f,т.е
y(t)=f[z(t),x(t)]
Y,
который определяется функцией выходов
f,т.е
y(t)=f[z(t),x(t)]
На множестве состояний автомата, состояние z(t0) определяется как начальное состояние. Автомат с несколькими входами и несколькими выходами удобно представить как автомат с одним входом и одним выходом.
Существует 3 способа задания конечных автоматов : 1.Табличный. 2.Графический. 3.Матричный
Пример 1 .Задана таблица переходов и таблица выходов.
|
X |
Z | ||||
|
z0 |
z1 |
z2 | |||
|
x1 |
z2 |
z0 |
z0 | ||
|
x2 |
z0 |
z2 |
z1 | ||
|
Таблица переходов | |||||
|
|
|
| |||
|
| |||||
|
| |||||
|
| |||||
|
x |
Z | ||
|
z0 |
z1 |
z2 | |
|
x1 |
y1 |
y1 |
y2 |
|
x2 |
y1 |
y2 |
y1 |
|
Таблица выходов | |||

X={x1,x2}
Z={z1,z2,z3}
Y={y1,y2}
Автомат Мили y(t)=f[z(t),x(t)]
Пример 2. Задана «отмеченная» таблица переходов
|
Выходной сигнал |
Y1 |
Y1 |
Y2 |
Y2 |
|
Состояние |
Z1 |
Z2 |
Z3 |
Z4 |
|
X1 |
Z2 |
Z3 |
Z1 |
Z2 |
|
X2 |
Z1 |
Z1 |
Z4 |
Z4 |
|
X3 |
Z2 |
Z3 |
Z2 |
Z1 |
11

 Автомат
Мура y(t)=f[z(t)]
Автомат
Мура y(t)=f[z(t)]
Матричное задание конечных автоматов
Матрица
соединений С=
![]() - есть квадратная матрица строки, которой
соответствуют исходным состояниям, а
столбцы состояниям перехода.
- есть квадратная матрица строки, которой
соответствуют исходным состояниям, а
столбцы состояниям перехода.
Для автомата Мили Сij=xk/ys, где xk - входной сигнал, вызывающий переход из состояния zi в zj, а ys- это выходной сигнал, выдаваемый на этом переходе
Пример 1(продолжение):
м атрица
соединений (входной сигнал в каждой
строке должен повторяться только один
раз!)
атрица
соединений (входной сигнал в каждой
строке должен повторяться только один
раз!)
Для автомата Мура элемент Сij равен множеству входных сигналов на переходе (zi , zj),а выходной сигнал определяется вектором выхода:
П ример
2(продолжение):
ример
2(продолжение):

Для конечных автоматов выполняется условие однозначности переходов. Автомат, который находиться в некотором состоянии под действием любого входного сигнала не может перейти более чем в 1 состояние.
При графическом способе задания это означает, что в графе автомата из любой вершины не может выходить 2 и более ребра, помеченных одним и тем же входным сигналом.
В матрице соединений в каждой строке входной сигнал не может повторяться более одного раза.
Частные случаи конечных автоматов.
1) Автомат без памяти Z= z : y(t)=f[x(t)]
2)
Автомат без входов X=Ǿ:
![]() z(t+h)=
z(t+h)=![]() [z(t)],
y(t)=f[z(t)]
[z(t)],
y(t)=f[z(t)]
3)
Автомат без выходов Y=Ǿ:
z(t+h)=![]() [z(t),x(t)]
[z(t),x(t)]
![]()
12
