28. Моделирование случайных событий. [1/2]

Для формализации случайных факторов и воздействий внешней среды используют случайные события, непрерывные и дискретные случайные величины, векторы и процессы. Простейшими случайными объектами прим моделировании являются случайные события.

1) Пусть имеются случайные числа , т.е. возможные реализации случайной величины, равномерно распределенной в интервале (0,1). Необходимо

реализовать событие А, которое наступает с заданной вероятностью р.

Определим А, как событие, состоящее в том , что выбранное значение (1) Тогда:,.

Процедура моделирования состоит в выборе значений и сравнение их ср.

Если неравенство (1) выполняется, то исходом испытания является событие А.

2) Пусть имеется полная группа событий , которые наступают с вероятностями. Определим- как событие, состоящее в том, что(2);.

Процедура моделирования состоит в последовательности сравнении случайных чисел со значением. Исходом испытания является событие, если выполняется неравенство (2). Эту процедуру называютопределение исхода испытания по жребию в соответствии с вероятностью .

3) Пусть имеется 2 зависимых события A, B, которые наступают с вероятностями P(A) и P(B). Условная вероятность наступления B: P(B/A) задана. Из последовательности {} выбирается, событие А- исход испытания. При выполнении неравенства.исходом испытания будетAB или . Если, не выполняется, исходом испытания является событие.

, - исходы испытания.

Схема моделирующего алгоритма:

46

РА=P_A;

РB=P_B;

XM=x_i;

XM1=x_i+1;

РBА=P(B/A);

;

KA=A;

;

KAB=AB;

47

29. Моделирование Марковских цепей. [1/1]

Простая однородная Марковская цепь задается матрицей переходов.

Она имеет вид: - вероятность из состоянияв состояние;;

Обозначим через вероятность того, что система будет находиться в состояниипослеn переходов . Пусть возможными исходами испытаний являются события. Вероятность- это условная вероятность наступления в данном испытании событияпри условии, что исходом предыдущего испытания было. Моделирование в цепи Маркова состоит в последовательном выборе событийпо жребию с вероятностями. Сначала определяется начальное состояние, задается начальными вероятностями. Для этого из последовательности чисел {} выбирается числои сравнивается с, где в качествевыступает. Выбирается номер, для которого справедливо неравенство(2). Тогда начальным событием реализации цепи будет событие. Выбирается следующие число из-и сравнивается с,где в качествебудут. Определяется номер,для которого справедливо неравенство (2), и следующее событиереализации цепей Маркова. Для эргодических Марковских цепей влияние начальных вероятностей быстро уменьшается, с ростом числа испытаний.

Эргодическим называют Марковский процесс, для которого предельное распределение вероятностей не зависит от начальных условий

.

48

30. Моделирование дискретных и непрерывных случайных величин с заданным законом распределения. [1/2]

Дискретная случайная величина принимает значение

с вероятностями , составляющими дифференциальное распределение вероятностей.

Интегральная функция распределения: .

Для получения дискретных случайных величин используют метод обратной функции. Искомое случайная величина ,где-функция обратная .-случайная величина равномерного распределения на (0,1).

Алгоритм вычисления:

- если , то, иначе

- если , то, иначе

…………………………………………………

- если , то, иначе…

Непрерывная случайная величина задана интегральной функцией распределения., где-плотность вероятности.

Для нахождения непрерывных случайных величин можно также использовать метод обратной функции. Чтобы получить число из последовательности

{}, которая имеет функцию плотности ,необходимо решитьотносительно уравнение :

Пример: Получить случайные числа с показательным (экспоненциальным) законом распределения :,;

- имеет равномерное распределение в интервале (0;1), следовательно .

49

Пример: Получить случайные числа равномерно распределенных на интервале (a,b).

; .

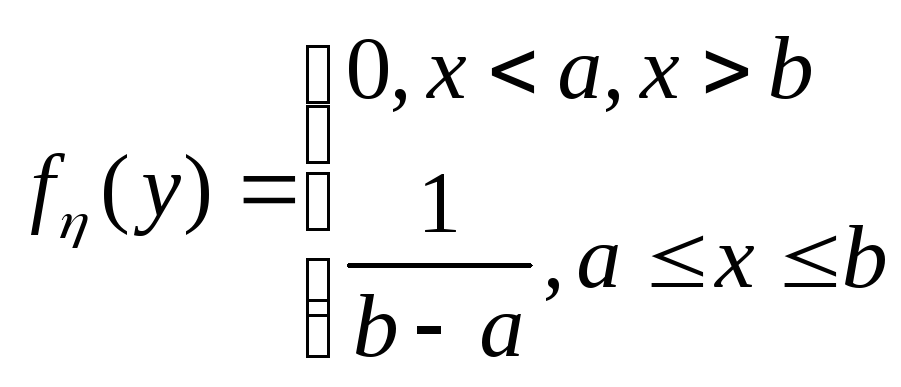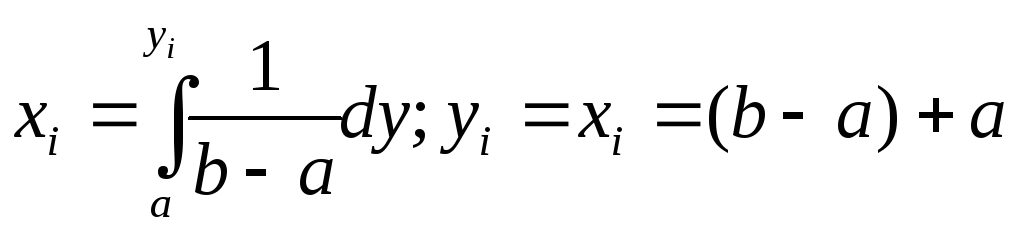Недостатки:

Этот способ получения случайных чисел с заданным законом распределения редко используется в силу двух недостатков:

1)интеграл (*) не всегда берется в конечном виде, приходиться прибегать к численным методам, что увеличивает затраты машинного времени.

2)даже если интеграл (*) берется в конечном виде, получается действие логарифмирования, извлечение квадратного корня, что также увеличивает затраты машинного времени.

50