Министерство образования и науки Российской Федерации

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

Расчет статической характеристики индуктивных датчиков линейных перемещений

Методические указания к расчетно-практическим работам

по курсу «Расчет элементов и устройств систем управления»

и для выполнения соответствующих разделов

дипломного проектирования для студентов специальности 210100

		Одобрено
		редакционно-издательским советом
		Балаковского института техники, технологии и управления

Балаково 2005

Цель методических указаний: ознакомление с конструкцией, принципом действия индуктивных датчиков линейных и угловых перемещений, основами расчета статической характеристики индуктивных датчиков.

Конструкция и принцип действия

В данной группе датчиков изменяющимся параметром управляемой цепи является индуктивное сопротивление X =L_x, где —частота переменного тока; L_x — индуктивность датчика, изменяющаяся при перемещении подвижной системы датчика.

Эти системы применяются лишь на переменном токе, величина которого будет изменяться при изменении Х=L_x.

Простейшим датчиком данной группы является дроссель с изменяющимся воздушным зазором (δ_B = var) или изменяющейся площадью его поперечного сечения (S_В = var)

Индуктивность дросселя при ненасыщенном магнитопроводе может быть выражена следующей формулой:

w - число витков обмотки дросселя;

R_m∑ — магнитное сопротивление сердечника и якоря;

δ_В —длина воздушного зазора, м;

S_B — площадь поперечного сечения воздушного зазора, м².

Для тока и тангенса угла сдвига фаз в цепи нагрузки имеем:

где R— активное сопротивление обмотки дросселя; Z_H=R_H+jL_Н — полное (комплексное) сопротивление нагрузки.

Таким образом, при изменении длины δ_в или площади поперечного сечения S_B воздушного зазора будет изменяться величина тока и угол сдвига фаз между векторами напряжения и тока.

Для определения пределов изменения тока в цепи нагрузки для магнитных систем при различных положениях якоря поступают следующим образом. Амплитуда тока в цепи нагрузки z_н, включенной последовательно с обмоткой датчика, равна

С другой стороны, , где значение магнитного потока Ф может быть выражено через магнитную индукцию В как Ф_m=B_mS; таким образом, или

.

Подставляя значение I_m и умножая на , находим

Из выражения

где

l_с—средняя длина магнитной силовой линии в сердечнике, м; S_c — площадь поперечного сечения сердечника, м², l_як — длина пути магнитного потока в якоре, м; S_як—площадь поперечного сечения якоря, м²; μ₀ — магнитщая проницаемость для материала сердечника при значении магнитной индукции В_m1; μ_як – то же для якоря при значении магнитной индукции в якоре В_m2.

Значения μ₀ и μ_як находят используя зависимость В_m = f(H_m), которая задается при помощи графиков или таблиц по формуле:

Далее имеем

Задаваясь значениями L_x, определяют величину B_m и соответствующие ей значения μ₀ и μ_як, затем рассчитывается величина , откуда определяется либо δ_вх, либо S_вх в зависимости от того, какая из них изменяется при Работе датчика.

При ненасыщенных системах

и расчет можно производить непосредственно по формуле

Кроме силы, обусловленной весом подвижной части, необходимо преодолевать силы притяжения, имеющие место в воздушном промежутке:

где G_в=—магнитная проводимость воздушного зазора.

Для случая, когда δ_в=var и имеют место плоские полюсные наконечники, т. е. тяговые усилия остаются неизменными при перемещении подвижных частей датчика:

С целью устранения отмеченного недостатка, а также для получения реверсивной характеристики датчика обычно применяют дифференциальную или мостовую схемы включения датчика.

Дифференциальная схема включения подобной системы с двумя дросселями показана на рис. 4-28,а, а мостовая — на рис. 4-28,6.

При любом значении воздушного зазора δ_В силы притяжения (которые не зависят в нашем случае от δ_в) будут почти полностью взаимно уравновешиваться. При передвижении подвижной части магнитной системы в этом случае приходится преодолевать лишь ее вес и силы трения, обусловливаемые весом.

В случае дифференциальной схемы токи для каждой из ветвей:

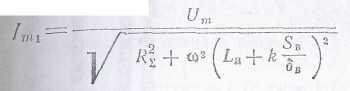
и

В зависимости от типа исполнительного устройства Z_H будет использоваться либо разность токов ΔI =I_m1-I_m2, либо их отношение I_m1/I_m2. На рис. 4-28, в показано изменение токов I_mi и I_m2 и величины ΔI в функции от длины воздушного промежутка δ_В.

В некоторых случаях может быть использован и угол сдвига фаз между векторами токов Ì_m1 и Ì_m2. Этот угол равен:

Применяются также исполнительные системы в виде одного (или двух) дросселей с воздушным зазором, в который вдвигается или выдвигается при действии датчика стальная пластинка. Происходящее при этом изменение L (или Z дросселя) и используется для управления электрической цепью переменного тока.

Показанный на рис. 4-29,б датчик может быть включен как индуктивный при использовании обмоток w₂. Если датчик питать через обмотку w₁,то при этом будет иметь место дифференциальная схема трансформаторного датчика.

Другим типом индуктивных датчиков является датчик, использующий изменение индуктивности соленоида вследствие изменения магнитной проницаемости или под влиянием изменения уровня ферромагнитных сыпучих тел:

где μ_x=f (μ, х, размеров зерен), S в м², l в м.

Пример. Определим индуктивность датчика, эскиз магнитной системы которого показан на рис. 4-30, а. Индуктивность датчика равна:

Где

1_С — средняя длина магнитных силовых линий в сердечнике:

-поперечное сечение сердечника:

-средняя длина магнитных линии в якоре:

- поперечное сечение якоря:

Значение μ₁ - магнитной проницаемости в магнитопроводе —

зависит от величины индукции В. Выбирая в качестве материала магнитной системы электротехническую сталь Э42,- а значение В=В_ml = [0,3 — 0,5] [тл], находим:

Индукция в якоре равна:

Индукции в якоре В_{т як} = 0,6 тл соответствует

Таким образом,

Следовательно, при δ = 0,05 см= 0,0005 м

Если площадь окна намотки равна Q = b*c=1*1,5= 1,5 с²,

Число витков

где q – площадь поперечного сечения провода:

f_о — коэффициент заполнения (определяемый из таблиц для

разных q).

Следовательно,

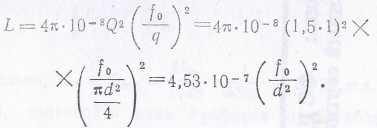
Из таблиц находим для провода ПЭ для d₁ = 0,1 мм = 0,01 см, что f₀ = 0,42 — 0,43 при дикой намотке и, следовательно

Для получения зависимости L = f (δ) (рис. 4-30, б), т. е. зависимости индуктивности датчика от величины воздушного зазора, может быть использовано следующее выражение для L:

Подставив различные значения δ_х, получим: при δ = 0.05 см = 0,05*10^-2 м; L_Х = 8 Гн; при δ _x = 0,03 см=0,03 *10^-2м имеем L_x = 14,2 Гн; при δ_x =0,07 см = 0,07*10^-2 м, имеем L_x =0,7 Гн и т. д.

Пример. Необходимо рассчитать характеристику управления (статическую характеристику) индуктивного датчика I_m = f(δ), т.е. определить зависимость между значением тока в цепи датчика и перемещением его якоря. Размеры магнитной системы датчика те же, что и в предыдущем случае. Напряжение U_m=36 В, сопротивление нагрузки R_H= 100 Ом.

Ток в цепи определится как

С другой стороны,

Наконец,

Зададим значение ωL_макс»R_∑, тогда и, следовательно, U_m = wωB_mS. Выбирая B_m = 1 тл, получаем, что

Для провода ПЭ получим число витков на 1 см² окна

Выберем d=0,29 мм, при котором w_о = 825.

Сопротивление обмотки датчика равно:

где

Расчет характеристики управления I_m =f(δ) можно провести в следующем порядке: задавая L_x = L, можно найти: и B_m, зная которое можно определить μ_с и μ_як , следовательно, отвечающее заданному L_x значение δ_Х

Так, при L_x ==0,5 Гн имеем, что

и, следовательно, В_m =B_{m c} = По кривой B_m = f(H_m), заданной в виде графиков или таблиц, находим Н_тс = 175 aв/м и .

Индукция в якоре при этом будет равна:

которой соответствует Н_{т як}=3 850 ав/м и, следовательно, μ_як= 320.

Значение

или

Тогда амплитуда тока при данном положении якоря, когда δ_х =0,1 мм, будет:

Аналогично, задаваясь другими значениями L_x, можно найти соответствующие им величины δ_х и I_m.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Конструкция и принцип действия. Типы датчиков.

2. Этапы расчета датчика.

3. Статическая характеристика датчика.

4. Расчет тяговой характеристики.

7. Способы получения реверсивной статической характеристики.

ОСНОВНАЯ ЛИТЕРАТУРА

1. Коновалов Л.И., Петелин. Элементы и системы электроавтоматики. М.: Высшая школа.1980.-192с.

2. Сотсков Б.С. Основы расчета и проектирование электромеханических элементов автоматики и телемеханических устройств. М.: Энергия, 1975.

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. Немцов М.В. Справочник по расчету параметров катушек индуктивности. М.:Энергоатомиздат,1989,192с.

ВРЕМЯ, ОТВЕДЕННОЕ НА ВЫПОЛНЕНИЕ РАБОТЫ

Подготовка к работе - 0,5 акад. час.

Выполнение работы – 1,0 акад. час.

Оформление отчета – 0,5 акад. час.