2.4. Плавание тел

По закону Архимеда на тело, погруженное в жидкость, действует выталкивающая сила, направленная вертикально вверх,

где W — объем погруженной части тела.

Вес воды, вытесняемой телом, полностью или частично погру­женным в воду, называется водоизмещением.

Центр тяжести вытесненного объема жидкости называется цент­ром водоизмещения или центром давления. При наклоне (крене) плавающего тела центр водо­измещения изменяет свое положение.

Линия, проходящая через центр тяжести тела и центр водоизмеще­ния в положении равновесия пер­пендикулярно свободной поверхности воды (плоскости плавания), явля­ется осью плавания. В положении рав­новесия ось плавания вертикальна, при крене она наклонена к вертикали под углом крена.

Точку пересечения подъемной силы Р при наклонном положении тела с осью плавания принято называть ме­тацентром. Расстояние между цент­ром тяжести тела и метацентром M обозначается через h_м (метацентрическая высота). Чем выше расположен метацентр над центром тяжести тела, т. е. чем больше метацентрическая высота , тем больше остойчивость тела (способность из крена переходить в положение равновесия), так как момент пары сил , стремящийся восстановить равновесие тела, прямо пропорционален метацентрической высоте. Величина метацентрической высоты может быть определена по формуле

где — момент инерции площади плоскости плавания относительно продольной оси ;

W — водоизмещение тела;

е — расстояние между центром тяжести и центром

водоизме­щения.

Если метацентр лежит ниже центра тяжести тела, т. е. метацентрическая высота отрицательна, то тело неостойчиво.

Примеры

2.30. Определить вес груза, установленного на круглом в плане металлическом понтоне диаметром , если после установки груза осадка понтона увеличилась на .

Решение. Вес груза равен дополнительной силе вытеснения воды. В соответствии с законом Архимеда дополнительная сила вытеснения воды определяется по формуле:

.

Следовательно, вес груза

.

Ответ: .

2.31. Простейший ареометр (прибор для определения плотности жидкостей), выполненный из круглого карандаша диаметром и прикреплённого к его основанию металлического шарика диаметром , имеет вес . Определить плотность жидкости , если ареометр цилиндрической частью погружается в неё на глубину .

Решение. Вес ареометра уравновешивается силой вытеснения (архимедовой силой).

Следовательно,

,

откуда найдем плотность жидкости

.

Ответ: .

2.32. Объём части ледяной горы, возвышающейся над поверхностью моря, равен . Определить общий объём ледяной горы и глубину её погружённой части, если в плане она имеет форму прямоугольника размером .

Решение. Общий вес ледяной горы

,

где - объём подводной части ледяной горы;

- плотность льда.

Сила вытеснения (подъёмная сила) по закону Архимеда

,

где - плотность морской воды.

При плавании ледяной горы соблюдается условие

;

,

отсюда

,

где ;

(табл. П-3).

Подставляя цифровые значения в предыдущую формулу, получим:

.

Общий объём ледяной горы

.

Глубина погружённой части ледяной горы

.

Ответ: ; .

2.33. Запорно-поплавковый клапан бака водонапорной башни имеет следующие размеры: d=100мм; l=68мм; мм; D=325мм. Если уровень воды не достигает полушара 2 , то клапан 1 открыт, и вода поступает в бак. По мере подъёма уровня воды и погружения в неё полушара на рычаг 3 начинает действовать сила , равная выталкивающей силе воды (по закону Архимеда). Через рычаг усилие передаётся на клапан. Если величина этого усилия превысит силу давления воды p на клапан, то он закроется и вода перестанет поступать в бак. Определить, до какого предельного давления p клапан будет закрыт, если допускается погружение в воду только полушара поплавка (до линии а – а).

Решение. Сила суммарного давления воды на клапан

,

где p – гидростатическое давление в корпусе клапана;

ω – площадь клапана.

Выталкивающая сила воды, действующая на поплавок, в соответствии с законом Архимеда

,

где - объём шара.

Составим сумму моментов сил относительно шарнира О

.

С учётом ранее полученных зависимостей запишем уравнение моментов

.

Отсюда находим предельное давление

Ответ: .

2.34. Автомобиль весом установлен на паром с размерами ; ; . Проверить остой­чивость парома, если его вес приложен на поло­вине его высоты, а центр тяжести автомобиля находится на высоте от верхней плоскости парома. Установить, как изменится метацентрическая высота , если на автомобиль будет уложен груз , центр тяжести которого расположен на высоте от верхней плоскости парома.

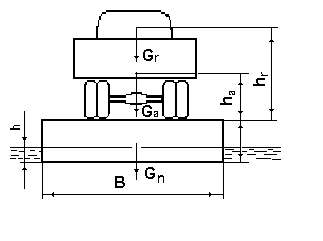
Решение. 1) Найдем положение центра тяжести парома с автомобилем (без груза) относительно нижней плоскости парома

2) Водоизмещение парома с автомобилем (объем воды, вытесненный паромом)

3) Осадка парома

4) Расстояние центра водоизмещения от нижней плоскости парома

5. Расстояние между центром тяжести и центром водоизмещения

5. Момент инерции площади плоскости плавания

5. Метацентрическая высота

Так как метацентрическая высота положительная, то паром остойчив. Для случая

нагруженного автомобиля аналогично находим:

Следовательно, при наличии груза на автомобиле метацентрическая высота уменьшается на

Но паром и при наличии груза будет остойчив.

Ответ: .