Ответ: Каноническое уравнение гиперболы .

Задача 3. Определить точки пересечения прямой и параболы .

Решение. Выразим y в уравнении прямой через х и подставим в уравнение параболы:

,

.

По теореме Виета , откуда Находим ординаты

Точки пересечения имеют координаты

.

Ответ: Точки пересечения прямой и параболы .

Задача 4. Установить, является ли линия 2-го порядка центральной и найти координаты ее центра.

Решение. Вычислим определитель матрицы квадратичной формы:

Так как , линия является центральной. Найдем координаты центра .

,

.

Ответ: Кривая второго порядка является центральной, центр С(3, -2).

Задача 5. Установить, приведением к каноническому виду какую кривую 2-го порядка определяет следующее уравнение: . Найти координаты центра (вершины), полуоси, эксцентриситет.

Решение. Выделим полные квадраты по х и у, так как член ху отсутствует в уравнении:

,

.

Делим обе части на свободный член:

.

Получим каноническое уравнение эллипса:

Центр С(3,-1), полуоси .

Ответ: Кривая центральная С(3,-1), .

Задача 6. Следующее уравнение привести к каноническому виду, определить его тип, изобразить на чертеже оси первоначальной и новой системы координат и построить кривую, соответствующую этому уравнению:

.

. Откуда следует, что кривая не является центральной.

Найдем собственные значения этой матрицы:

,

,

.

Найдем собственные векторы, соответствующие найденным собственным значениям.

1. .

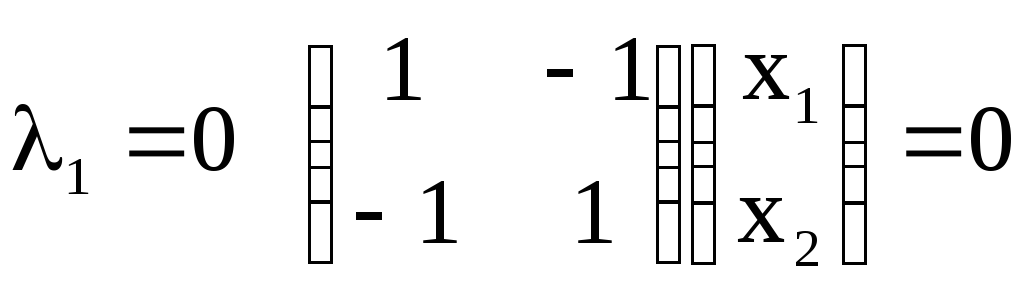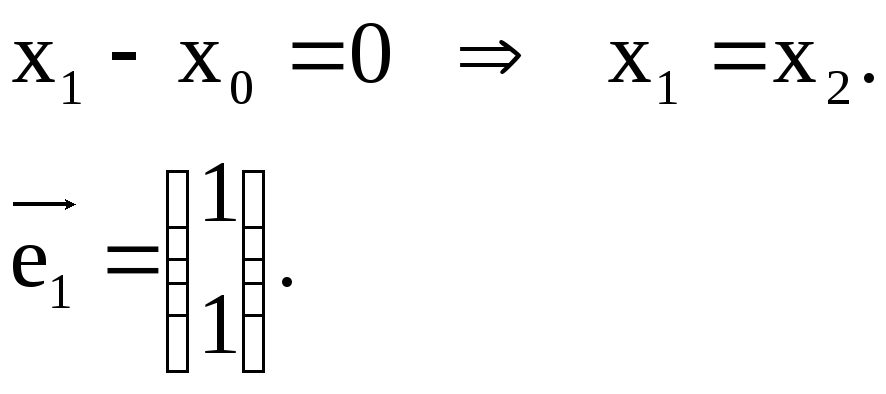
2.

Проверим что означает: ориентация правильная, совпадает с исходным базисом.

Нормируем векторы и вычислим базисные векторы новой системы координат:

Уравнение в новом базисе имеет вид

.

Системы координат ХОУ с базисом и с базисом связаны формулами

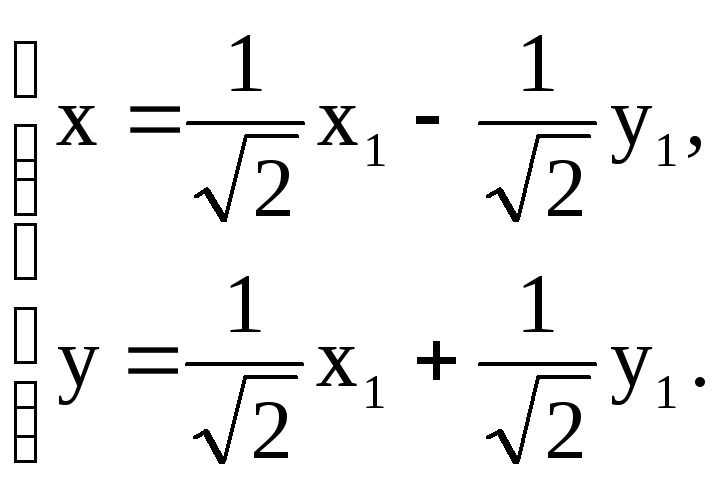
Подставляя в исходное уравнение вместо х и у их выражения, получим

или

.

Выделяя полный квадрат по у, получим

Эта парабола симметрична относительно оси (рис.12), О₁ – вершина, находящаяся в точке . В новой системе координат уравнение примет вид

.

Y

O₁

О Х

Рис. 12