16 Координатная форма скалярного произведения

ТЕОРЕМА 16.1. Пусть в пространстве выбран ортонормированный базис , в котором . Тогда

Доказательство. По определению координат вектора в базисе имеем  и , поэтому Используя доказанные свойства скалярного произведения, получаем Поскольку базис  ортонормированный, то  и , значит, окончательно получим Теорема доказана. Замечание 16.1. Если рассматривается множество векторов, параллельных некоторой плоскости (т.е. двумерное векторное подпространство пространства ), то формула  принимает вид

где  в ортонормированном базисе двумерного подпространства .

17 Задачи, решаемые с помощью скалярного произведения

Задача 17.1. Пусть даны координаты вектора  в ортонормированном базисе. Найти длину вектора . Решение. Согласно свойству 4. скалярного произведения длина вектора находится по формуле , т.е. . Но скалярное произведение векторов в ортонормированном базисе вычисляется по формуле . Поэтому получаем следующую формулу для нахождения длины вектора, заданного своими координатами в ортонормированном базисе

Задача 17.2. Пусть даны координаты векторов  и  в ортонормированном базисе. Найти угол между векторами  и . Решение. Из определения скалярного произведения получаем следующую формулу для нахождения косинуса угла между векторами:

С учетом формул  и  приходим к следующей формуле для нахождения угла между векторами, заданных своими координатами в ортонормированном базисе

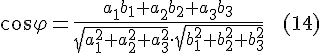
Ортогональная проекция вектора на ось.

Задача 17.3. Пусть даны два вектора  и . Найти ортогональную проекцию вектора  на ось вектора . Решение. По формуле  имеем 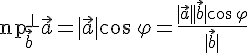Следовательно, получаем формулу для нахождения ортогональной проекции вектора  на ось вектора 

Ортогональная проекция вектора на плоскость.

Определение 17.1. Пусть дан вектор  и некоторая плоскость . Обозначим через  ортогональные проекции точек  на плоскость . Вектор  называется ортогональной проекцией вектора  на плоскость  и обозначается . Задача 17.3. Найти ортогональную проекцию данного вектора  на плоскость , перпендикулярную данному вектору . Решение. Пусть данный вектор . По определению ортогональной проекции вектора на плоскость имеем  (см рисунок). По правилу многоугольника для сложения векторов, получаем равенство Заметим, что  и , поэтому . По признаку коллинеарности векторов получаем равенство . Кроме того, , поэтому Умножим обе части этого равенства скалярно на вектор . Имеем числовое равенство  Учитывая, что   Из последнего равенства находим, что  Поэтому для нахождения ортогональной проекции вектора на плоскость, перпендикулярную заданному вектору имеем 

18 Геометрический смысл координат вектора в ортонормированном базисе

Пусть в пространстве выбран ортонормированный базис , в котором . Тогда . Умножим обе части этого равенства скалярно сначала на вектор , потом на  и . Получаем Поскольку базис ортонормированный, то , а поэтому имеем равенства С учетом формулы  имеем Из равенств  получаем геометрический смысл координат вектора в ортонормированном базисе: координаты вектора в ортонормированном базисе равны ортогональным проекциям данного вектора на оси соответствующих базисных векторов. Обозначим через . Тогда, используя формулу , равенства  примут вид

Числа  называются направляющими косинусами вектора  в ОНБ . Подставим  в  получаем

или

Таким образом, сумма квадратов направляющих косинусов любого ненулевого вектора равна единице.

Заметим, что если  --- единичный, то его координаты в ОНБ равны направляющим косинусам этого вектора или, иначе, направляющие косинусы данного вектора  равны координатам единичного вектора  того же направления.