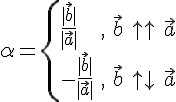
6 Признак коллинеарности векторов.

ТЕОРЕМА 6.1. Пусть . Тогда Доказательство необходимости. Существование докажем конструктивно, т.е. укажем число удовлетворяющее условиям теоремы. Положим Легко проверить, что векторы  и  имеют одинаковые длины и направления. Следовательно, . Докажем теперь единственность. Пусть существует еще число  такое, что . Тогда имеем равенство   так как . Доказательство достаточности. Непосредственно следует из определения произведения вектора на число.

7 Компланарные векторы. Признак компланарности векторов.

Определение 7.1. Вектор  называется параллельным плоскости , если прямая  либо параллельна плоскости , либо лежит в ней. Нулевой вектор параллелен любой плоскости. Определение 7.2. Векторы  называются компланарными, если существует плоскость, которой они параллельны. ТЕОРЕМА 7.1. Пусть векторы  такие, что  неколлинеарен . Векторы  компланарны тогда и только тогда, когда существуют и определены однозначно числа  и  такие, что выполняется равенство . Доказательство необходимости. Существование. От произвольной точки  отложим векторы  и . Так как векторы  компланарны, то точки  лежат в одной плоскости, а точки  не лежат на одной прямой ( неколлинеарен ). Рассмотрим возможные случаи расположения точки . 1.  не лежит на прямых  и .Через точку  проведем прямые  параллельные прямым  и  соответственно, где .  По правилу параллелограмма сложения двух неколлинеарных векторов имеем . Но точки , значит . По теореме 6.1. получаем, что , т.е. . 2. . В этом случае  и по теореме 6.1. получаем, что . Полагая , снова приходим к требуемому равенству. 3. . Этот случай рассматривается аналогично случаю 2. Итак, существование чисел  и  доказано. Переходим к доказательству их единственности. Предположим, что существуют еще числа  и , удовлетворяющие условию теоремы. Тогда имеем равенство Если бы , то имело бы место равенство из которого следовало бы по теореме 6.1., что . Но это противоречит условию. Следовательно, . Аналогично можно доказать, что . Необходимость доказана. Доказательство достаточности. Пусть имеет место равенство . Отложим от некоторой точки  вектор , затем от точки  вектор . Тогда . Рассмотрим плоскость, содержащую три точки , обозначим ее через . Тогда получаем, что векторы параллельны этой плоскости. Но тогда плоскости  параллельны также векторы , т.е. они компланарны по определению. Теорема доказана полностью. Для дальнейшего изложения нам потребуется еще одна теорема, доказательство которой предлагаем провести самостоятельно в полной аналогии с доказательством теоремы 7.1. ТЕОРЕМА 7.2. Если векторы  некомпланарны, то для любого вектора  имеет место равенство

8 Линейная зависимость и независимость системы векторов.

В этом параграфе рассматривается произвольное векторное пространство (см. Замечание 5.1.) Определение 8.1. Пусть дана система векторов

 

Говорят, что вектор  является линейной комбинацией векторов системы  с коэффициентами , если справедливо равенство

Говорят еще, что вектор  линейно выражается через векторы системы . Определение 8.2. Векторы системы  называются линейно независимыми, если равенство

выполняется тогда и только тогда, когда все  равны нулю. Отметим, что набор чисел  является нулевым тогда и только тогда, когда все числа этого набора равны нулю. В противном случае, набор чисел считается ненулевым. Определение 8.3. Векторы системы  называются линейно зависимыми, если существует хотя бы один ненулевой набор  такой, что имеет место равенство . Свойства линейной зависимости. 1. Система векторов, содержащая , линейно зависима. Действительно, справедливо равенство  2. При  система векторов  линейно зависима тогда и только тогда, когда хотя бы один из них является линейной комбинацией остальных. В самом деле, пусть система векторов  линейно зависима. Тогда по определению выполнено равенство , причем, например, . Перепишем это равенство в виде . Получаем, что  является линейной комбинацией векторов . Обратно, пусть, например,  является линейной комбинацией векторов . По определению это означает, что имеем равенство , которое равносильно равенству . Заметим, что набор чисел  --- ненулевой, поэтому система векторов  линейно зависима. 3. Если подсистема системы векторов  линейно зависима, то и вся система  линейно зависима. Пусть дана система векторов  и пусть для определенности первые  векторов линейно зависимы. Тогда по определению существует ненулевой набор чисел  такой, что имеет место равенство . Но тогда, очевидно, имеет место и равенство . Для завершения доказательства осталось заметить, что набор чисел  также ненулевой. 4. Если система векторов  линейно независима, то и любая ее подсистема линейно независима. Доказательство сразу получается методом от противного из доказанного свойства 3.