25 Площадь ориентированного параллелограмма. Вычисление площадей.
Определение
25.1. Пусть 
и 
два
вектора, параллельные некоторой
ориентированной плоскости
(ориентация
определяется некоторым
базисом 
).
Площадью
ориентированного параллелограмма 
,
построенного на векторах 
и 
называется
число 
,
определяемое следующим образом:
1. 
,
если базис 
положительно
ориентирован;
2. 
,
если базис 
отрицательно
ориентирован;
3. 
,
если векторы 
и 
коллинеарны.
Очевидно,
что 
.
Пусть 
будет
единичный вектор, перпендикулярный
нашей плоскости и направленный в ту
сторону, с которой мы смотрим на нее;
тогда 
.
Если тройка векторов 
правая,
то 
и
параллелограмм 
ориентирован
положительно, т.е 
.
Если тройка векторов 
левая,
то 
и
параллелограмм 
ориентирован
отрицательно, т.е 
.
В том и другом случае
Из этого легко усмотреть следующие свойства ориентированной площади
1. 
.
2. 
.
3. 
.
4. 
.
Зададим
теперь векторы 
и 
их
координатами относительно базиса 
:
Тогда
В силу свойств ориентированной площади получаем
Учитывая,
что 
и 
,
получим
Обозначим
через 
,
т.е. площадь параллелограмма, построенного
на базисных векторах. Тогда получаем,
что
Пусть
теперь на плоскости задана аффинная
система координат 
.
ТЕОРЕМА
25.1. Площадь 
треугольника 
,
заданного своими вершинами 
относительно
аффинной системы координат 
на
плоскости вычисляется по формуле
(
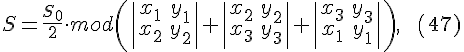
--- знак
модуля или абсолютной величины)
Доказательство. Из
предыдущих рассуждений следует, что 
.
Поскольку 
(см.
формулу 
),
то с учетом 
получаем
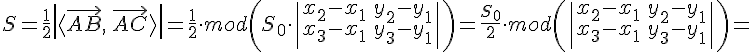
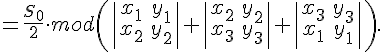
ТЕОРЕМА
25.2. Для
того чтобы три точки 
относительно
аффинной системы координат 
,
принадлежали одной прямой, необходимо
и достаточно, чтобы выполнялось равенство
или
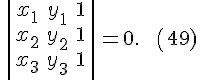
Замечание
25.1. Если
заданы метрические коэффициенты 
базиса 
,
входящего в систему координат 
,
то площадь 
,
как легко видеть, вычисляется по
формуле 
,
где 
.
Поэтому формулу 
можно
записать в виде
