22 Векторное произведение векторов.
Пусть
векторное пространство 
ориентировано
правой тройкой (см. определение 21.3).
Определение
22.1. Векторным
произведением двух неколлинеарных
векторов 
и 
,
взятых в данном порядке,
называется
вектор 
,
удовлетворяющий следующим трем условиям:
1. 
,
где 
---
угол между векторами 
и 
;
2. 
;
3. 
---
правая тройка
Векторное произведение коллинеарных векторов считается равным нулевому вектору.
Дадим
еще конструктивное определение векторного
произведения, то есть укажем способ
построения по данным векторам 
и 
вектора
их векторного произведения 
.
Предположим,
что данные вектора 
и 
отложены
от некоторой точки 
.
Выполним следующие построения:
1. Через
точку 
проводим
плоскость 
;
2. Ортогонально
проектируем вектор 
на
плоскость 
и
получаем вектор 
;
3. Строим
вектор 
;
4. В
плоскости 
поворачиваем
вектор 
по
часовой стрелке (если смотреть из конца
вектора 
)
на 
и
получаем вектор 
Нетрудно
видеть, что 
.
Свойства векторного произведения.
1. Векторное произведение векторов антикоммутативно, т.е.
Доказательство. Непосредственно следует из определения векторного произведения.
2. Числовой множитель можно выносить за знак векторного произведения (векторное произведение однородно по каждому аргументу), т.е.
Доказательство. Введем следующие обозначения:
Пусть 
---
угол между векторами 
и 
.
Отметим, что 
.
Нам необходимо доказать, 
.
Сначала покажем, что векторы 
и 
сонаправлены.
Рассмотрим возможные случаи:
(a) Если 
или
хотя бы один из векторов 
и 
нулевой,
то доказываемое свойство очевидно.
(b) Пусть 
.
Тогда 
и
так как 
,
то 
.
Следовательно, 
.
(c) Пусть 
.
Тогда 
и
так как 
,
то
.
Следовательно, 
.
Покажем,
что 
.
Действительно,
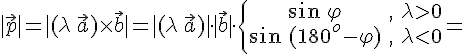
3. Векторное произведение линейно по каждому аргументу, т.е.
Доказательство.
Легко усматривается из рисунка, используя
конструктивное определение векторного
произведения. Действительно, отложим
векторы 
и 
от
одной точки 
и
обозначим через 
(диагональ
параллелограмма, построенного на
векторах 
и 
как
на сторонах и выходящая из точки 
.
Далее проектируем параллелограмм,
построенный на векторах 
и 
,
как на сторонах на плоскость 
,
проходящую через точку 
и
перпендикулярную вектору 
.
Получаем параллелограмм со сторонами 
и 
,
причем вектор 
проектируется
в вектор 
,
являющийся диагональю последнего. Затем
"растягиваем" этот параллелограмм
в 
раз
и получаем параллелограмм со
сторонами 
и 
и
диагональю 
.
Наконец, поворачиваем последний в
плоскости 
на 
по
часовой стрелке и получаем параллелограмм
со сторонами 
и 
и
диагональю 
.
Согласно
конструктивному определению векторного
произведения имеем:
С
другой стороны, по правилу сложения
векторов имеем 
Осталось
вспомнить, что 
.
4. Векторное произведение двух векторов равно нулевому вектору тогда и только тогда, когда данные векторы коллинеарны, т.е.
Доказательство. Действительно, пусть
5. Длина
вектора векторного произведения двух
неколлинеарных векторов 
и 
равна
площади параллелограмма, построенного
на этих векторах как на сторонах.
Доказательство. Следует из условия 1. определения векторного произведения векторов.