20 Скалярное произведение на плоскости в аффинных координатах.

Пусть на плоскости введен произвольный аффинный базис . Введем следующие обозначения для скалярных квадратов базисных векторов и самого скалярного произведения данных векторов: Из свойств скалярного произведения следует, что . Совокупность чисел  будем называть метрическими коэффициентами базиса .

Наряду с базисом  рассмотрим еще базис .

Определение 20.1. Базисы  и  называются взаимными, если

В случае двумерного векторного подпространства (множества векторов параллельных некоторой плоскости) взаимные базисы допускают простую геометрическую интерпретацию. Другими словами, можно указать способ построения взаимного базиса к заданному. Действительно, пусть  --- данный базис. Тогда вектор  перпендикулярен вектору  и образует острый угол с вектором  , и, аналогично,  перпендикулярен вектору  и образует острый угол с вектором . Длины векторов  определятся условием .

Точно так же определим метрические коэффициенты  базиса .

Рассмотрим произвольный вектор  плоскости и разложим его по векторам  и . Получим

Определение 20.2. Коэффициенты  называются контравариантными координатами , а  --- ковариантными координатами вектора  в базисе .

Рассмотрим теперь два вектора  и  , разложим их по векторам , а также по векторам :

Используя данные представления векторов  и , вычислим их скалярное произведение четырьмя способами:

Мы видим, что удобнее всего находить скалярное произведение двух векторов, если один вектор задан ковариантными, а другой контравариантными координатами. Установим связь контравариантных координат  с ковариантными координатами  одного и того же вектора . Из соотношения  находим

или

или короче

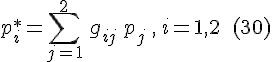
Аналогично находим

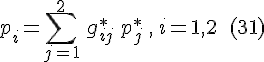
Установим связь между взаимными базисами. Для этого разложим базисные векторы  по векторам :

Умножая скалярно обе части первого из этих соотношений на  и , получим

и аналогично из второго соотношения

Мы приходим к формулам:

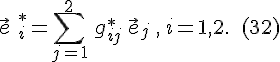
Подобным образом выводится соотношение

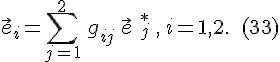
Найдем теперь формулы для вычисления метрических коэффициентов взаимного базиса, по известным метрическим коэффициентам исходного базиса. Для этого распишем формулы  подробно. Получаем:

Умножая скалярно обе части каждого из этих соотношений на  и , получим

Используя ранее введенные обозначения и определение взаимных базисов, приходим к следующей системе линейных уравнений относительно неизвестных 

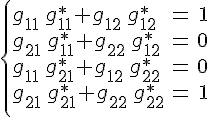
Решая эту систему приходим к следующим выражениям для метрических коэффициентов взаимного базиса с учетом, что  и 

где  .

21 Ориентация плоскости и пространства.

Для простоты вычислений рассмотрим подробно как определяется ориентация плоскости. Пусть  --- множество всех векторов, параллельных плоскости, т.е. двумерное подпространство пространства . Как известно, любые два неколлинеарных вектора из , взятые в определенном порядке, образуют базис . Поэтому в  существует бесконечное множество базисов. Рассмотрим два из них:  и . Разложим векторы базиса  по векторам базиса :

Из координат векторов  и  можно составить матрицу второго порядка:

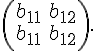
Координаты вектора  образуют первый столбец этой матрицы, а координаты вектора  --- второй столбец. Эту матрицу назовем матрицей перехода от базиса  к базису .

Определение 21.1. Число  называется определителем матрицы перехода от базиса  к базису  и обозначается так:

Так как векторы  и  линейно независимы, то из следствия о координатах коллинеарных векторов получаем, что . Рассмотрим некоторые свойства определителей матрицы перехода от одного базиса к другому. 1. Для любого базиса  имеем .

В самом деле,  поэтому

2. Для любых трех базисов  справедливо равенство

Пусть . Подставив в правые части этих формул вместо  и  их разложения по формулам , будем иметь:

Отсюда получаем определитель матрицы перехода от базиса  к базису :

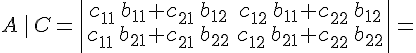
поскольку определитель матрицы перехода от базиса  к базису  имеет вид:

3. Для любых базисов  справедливо равенство

Действительно, если в равенстве  положить  и воспользоваться свойством 1., то получим требуемое.

Обозначим через  множество всех базисов подпространства . Будем говорить, что базисы  находятся в отношении  ( одинаково ориентированы), если , записываем так . Докажем, что отношение  является отношением эквивалентности на множестве  всех базисов подпространства . Для этого необходимо проверить, что отношение  удовлетворяет свойствам рефлексивности, симметричности и транзитивности.

1.рефлексивность. Для произвольного базиса  по свойству 1 имеем:

2.симметричность. Пусть . Но из свойства 3 следует, что 

3. транзитивность. Непосредственно следует из свойства 2.

Докажем, что фактор-множество  состоит лишь из двух элементов. Для этого рассмотрим базисы  и $\bar A=\{\vec a_2;\vec a_1\}$ . Так как  то классы эквивалентности  и  различны. Легко убедиться, что любой базис  принадлежит либо классу , либо классу . В самом деле, по свойству 2 . Но , поэтому , отсюда либо , либо .

Каждый из элементов фактор-множества  называется ориентацией векторного подпространства . Выделим одну из этих ориентаций, назовем ее положительной ( а другую - отрицательной). Векторное подпространство, в котором выбрана положительная ориентация, называется ориентированным. Базисы положительной ориентации называют правыми базисами, а базисы отрицательной ориентации - левыми.

Аналогичным образом определяется ориентация векторного пространства . А именно,как известно, любые три некомпланарных вектора из , взятые в определенном порядке, образуют базис . Поэтому в  существует бесконечное множество базисов. Рассмотрим два из них:  и . Разложим векторы базиса  по векторам базиса :

Из координат векторов  и  можно составить матрицу третьего порядка:

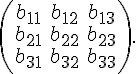
Координаты вектора  образуют первый столбец этой матрицы, координаты вектора  --- второй столбец, а координаты вектора  --- третий столбец. Эту матрицу назовем матрицей перехода от базиса  к базису . Определение 21.2. Число 

называется определителем матрицы перехода от базиса  к базису  и обозначается так:

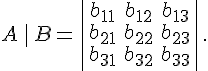
Так как векторы  и  линейно независимы, то можно показать, что .

Точно так же проверяются свойства определителей матриц перехода и доказывается, что существуют всего две различные ориентации векторного пространства . В дальнейшем будем считать, что векторное пространство ориентировано и положительную ориентацию определяет правая тройка векторов.

Определение 21.3. Тройка некомпланарных векторов, взятых в данном порядке, называется правой (левой), если кратчайший поворот от первого вектора ко второму виден из конца третьего совершающимся против (по) часовой стрелке, при условии, что векторы приведены к общему началу.