19 Системы координат на плоскости и в пространстве. Основные задачи на метод координат

Определение 19.1. Пусть  --- произвольная точка и  --- произвольный базис в пространстве. Четверка  называется аффинной системой координат в пространстве или аффинным репером. Четверка  называется прямоугольной декартовой системой координат (сокращенно ПДСК ).

Определение 19.2. Направленные прямые, проходящие через точку  и параллельные координатным векторам, на которых положительные направления определяются этими векторами называются координатными осями.

Координатная ось параллельная первому базисному вектору называется осью абсцисс и обозначается , координатная ось параллельная второму базисному вектору называется осью ординат и обозначается , координатная ось параллельная третьему базисному вектору называется осью апликат и обозначается .

Плоскости, определяемые парами координатных осей называются координатными плоскостями.

Замечание 19.1. На плоскости также имеем две системы координат:

1.  --- аффинная система координат (сокращенно А.С.К).

2.  --- прямоугольная декартова система координат.

Определение 19.3. Пусть  --- А.С.К,  --- произвольная точка пространства. Вектор  называется радиус-вектором точки .

Определение 19.4. Координаты радиус-вектора  в базисе  называются координатами точки  в системе координат .

Кратко:  в системе  по определению означает выполнение равенства

. Аналогично на плоскости: любая точка  имеет пару координат в репере, которые есть координаты ее радиус-вектора в соответствующем базисе.

Нетрудно показать, что между точками пространства (плоскости) и упорядоченными тройками (парами) чисел существует взаимно однозначное соответствие. Решим несколько задач.

Задача 19.1. В аффинной системе координат  даны координаты точек  и . Найти координаты вектора.

Решение. По правилу вычитания векторов получаем . Откуда получаем, что каждая координата вектора равна разности соответствующих координат конца и начала вектора, т.е.

Задача 19.2. В прямоугольной декартовой системе координат  даны координаты точек  и . Найти расстояние между точками  и .

Решение. Очевидно, что расстояние между данными точками  и  равно длине вектора . Поэтому по формуле  имеем . С учетом формул  и , окончательно получаем

Деление отрезка в данном отношении.

Определение 19.5. Пусть  --- две точки, а  --- некоторое действительное число . Говорят, что точка  делит направленный отрезок  в отношении , если

Из  следует, что , то есть , причем:

если ;

если  лежит вне отрезка .

Задача 19.3. В аффинной системе координат , точка  делит направленный отрезок  в отношении . Найти координаты точки .

Решение. Пусть  тогда переписав  в координатах, с учетом  получим равенства:

или после очевидных преобразований

В частности, если  --- середина отрезка, то есть , то формулы  приобретают вид:

Задача 19.4. В аффинной системе координат  даны координаты вершин треугольника . Найти координаты точки  --- точки пересечения его медиан (центр тяжести треугольника).

Решение. Пусть  --- середина отрезка . Тогда точка  делит направленный отрезок  в отношении . Последовательно, применяя формулы  и  получим:

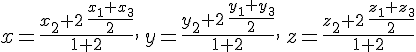 и  Окончательно имеем формулы нахождения координат центра тяжести треугольника по известным координатам его вершин: