
- •3. Матрицы
- •3.22. Решите матричное уравнение:
- •4. Системы линейных уравнений
- •5. Задачи на отыскание собственных значений и собственных векторов матриц
- •5.5. При каком значении параметра матрица имеет собственный вектор , соответствующий собственному значению ?
- •5.8. Проверьте, что вектор является собственным вектором матрицы и найдите соответствующее ему собственное значение .: , .
- •6. Предел последовательности.
- •7. Предел функции.
- •8. Производная функции
- •10. Графики функций
- •11. Интеграл
- •13. Частные производные. Градиент. Производная по направлению.
- •14. Первый и второй дифференциал. Касательная плоскость.
- •16. Локальный экстремум функции нескольких переменных.
- •17. Локальный условный экстремум функции нескольких переменных.
3. Матрицы
3.9. Найдите ранг системы векторов и укажите какой-нибудь базис в этой системе векторов
а)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
б)
![]() ,
,
![]() ,
,
![]() ,
,
![]()
в)
![]() ,
,
![]() ,
,
![]() ,
,
![]()
г)
![]() ,
,
![]() ,
,
![]() ,
,
![]()
3.21. Найдите
значения параметров
![]() ,
,
![]() и
и
![]() ,
при которых матрицы
,
при которых матрицы
![]() и
и
![]() являются
обратными:
являются
обратными:
а)
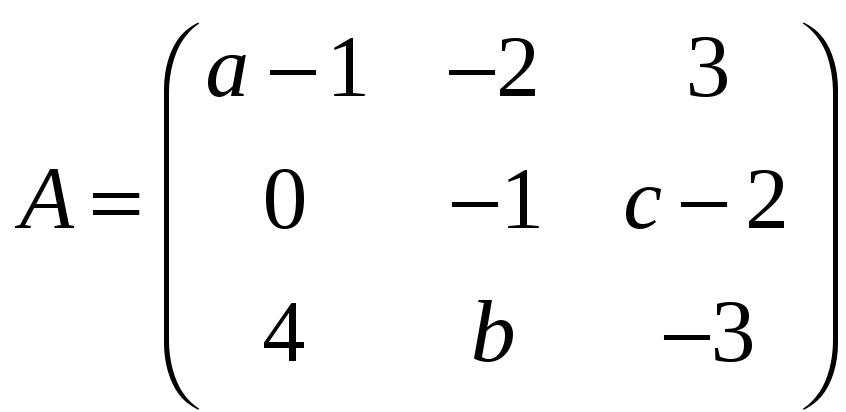 ,
,
 ;
;
б)
 ,
,
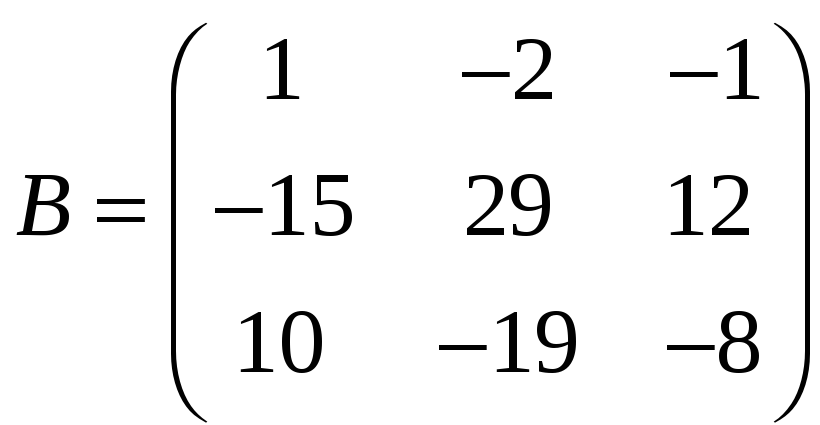 ;
;
в)
 ,
,
 ;
;
г)
 ,
,
 .
.
3.22. Решите матричное уравнение:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
 ;
;
д)
 ;
е)
;
е)
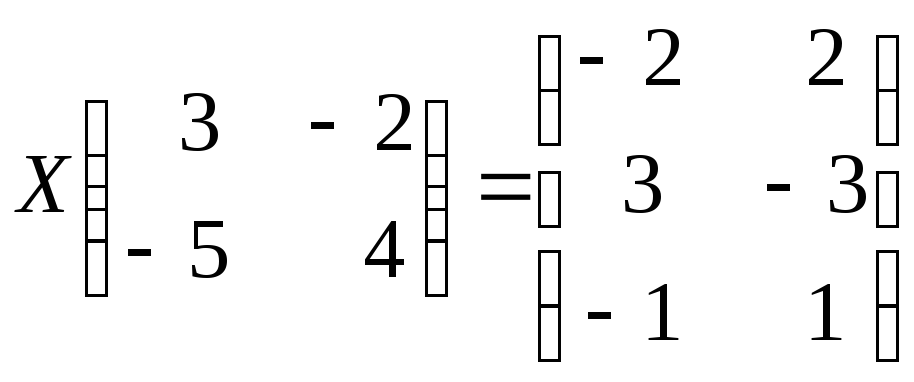 ;
ж)
;
ж) ;
з)
;
з)
и)
![]() ;
к)
;
к)
![]()
Ответы: 3.21. а)
![]() ,
,
![]() ,
,
![]() ;
б)
;
б)
![]() ,
,
![]() ,
,
![]() ;
в)
;
в)
![]() ,
,
![]() ,
,
![]() ;
г)
;
г)
![]() ,
,
![]() ,
,
![]() .
3.22. а)
.
3.22. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
 ;
д)
;
д)
 ;
;
е)
 ;
ж)
;
ж)
 - ???; з)
- ???; з)
![]() ;
и)
;
и)
![]() ;
к)
;
к)
![]() .
.
4. Системы линейных уравнений
4.1. Решите систему уравнений:
а)
 ;
б)
;
б)
 ;
в)
;
в)
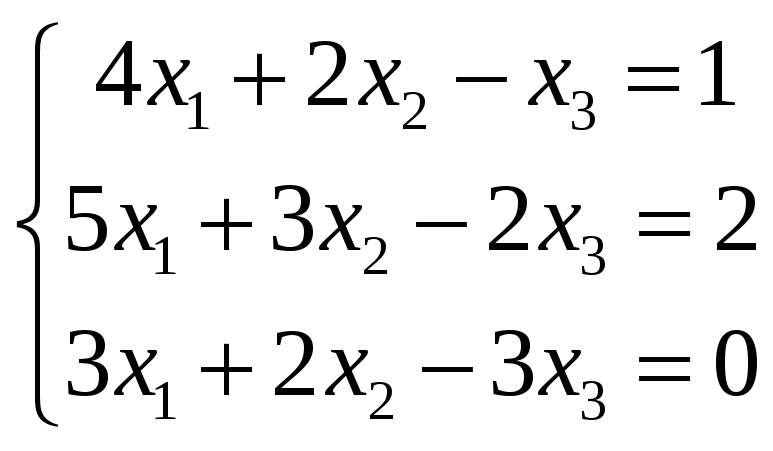 ;
г)
;
г)
 .
.
4.2. Найдите фундаментальную систему решений:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)

4.3.
Найдите фундаментальную систему решений
однородной системы линейных уравнений.
Запишите ответ в векторном виде. а)
 ;
;
б)
 ;
в)
;
в)
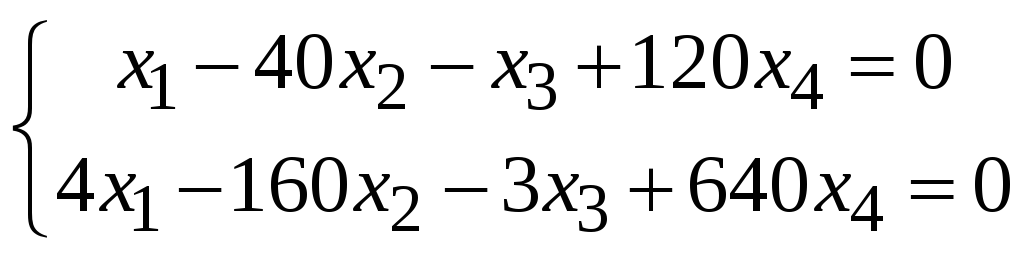 ;
;
г)
 ;
д)
;
д)
 ;
е)
;
е)
 ;
;
ж)
 ;
з)
;
з)
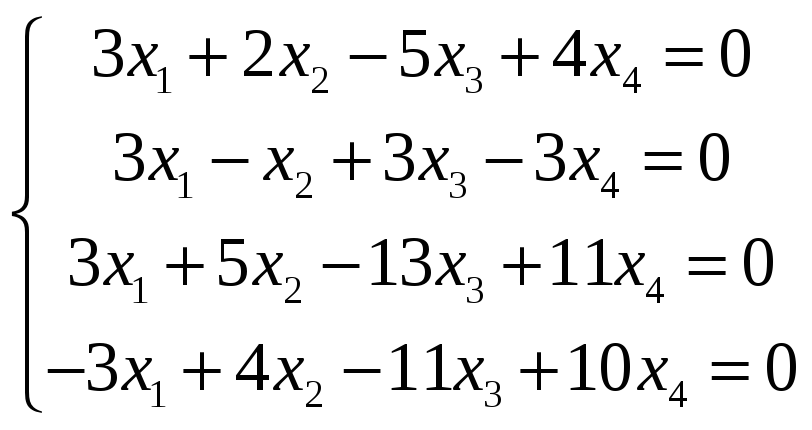 .
.
4.6. Представьте общее решение в виде суммы частного решения и общего решения соответствующей однородной системы
а)
 ;
б)
;
б)
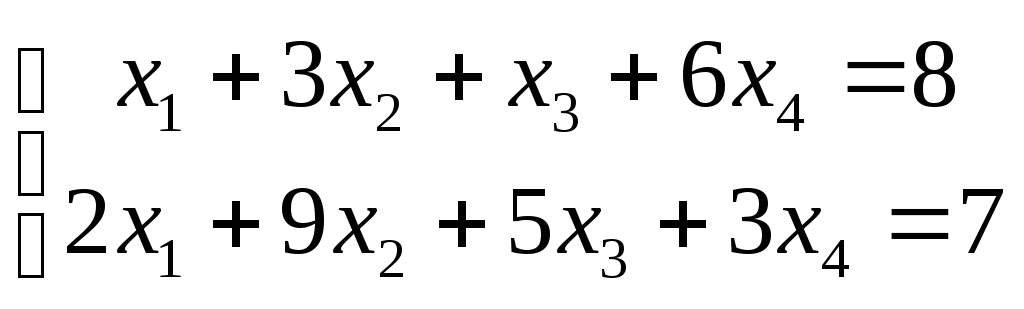 ;
в)
;
в)
 ;
;
г)
 ;
д)
;
д)
 ;
е)
;
е)
 ;
;
ж)
 ;
з)
;
з)
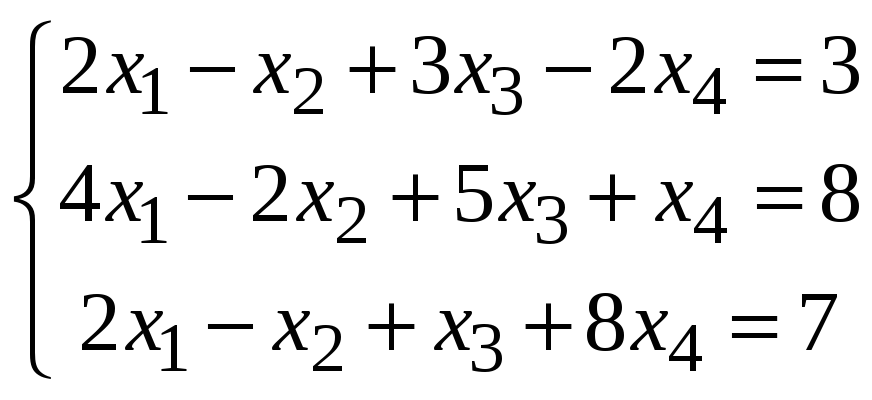 ;
и)
;
и)

4.7.
При каких значениях параметра a
однородная
система линейных уравнений, заданных
матрицей
 ,
имеет ненулевое решение?
,
имеет ненулевое решение?
Ответы: 4.1.
а)
![]() ,
,
![]() ,
,
![]() ;
б)
;
б)
![]() ,
,
![]() ,
,
![]() ;
в)
;
в)
![]() ,
,
![]() ,
,
![]() ;
;
г)
![]() ,
,
![]() ,
,
![]() ;
4.2.
а)
;
4.2.
а)
![]() ;
г)
;
г)
![]() .
.
4.3.
а)
 ;
з)
;
з)
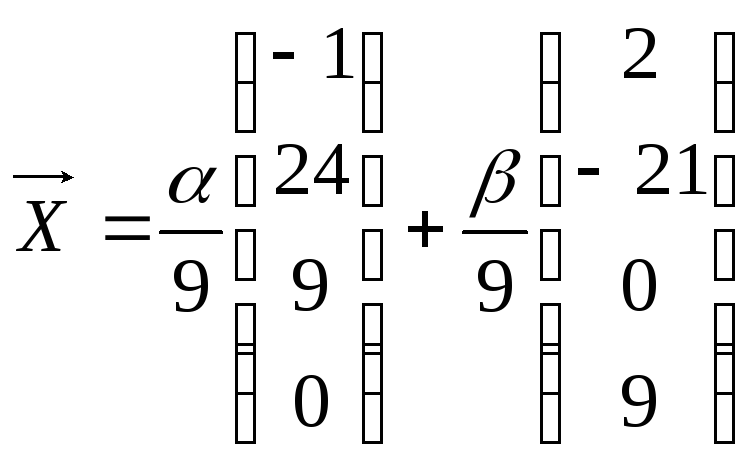 .
.
4.6.
а)
 ;
и)
;
и)
 .
4.7.
.
4.7.
![]() .
.
5. Задачи на отыскание собственных значений и собственных векторов матриц
5.2. Найдите
![]() ,
где
,
где
![]() -
угол между собственными векторами,
соответствующими различным собственным
значениям: а)
-
угол между собственными векторами,
соответствующими различным собственным
значениям: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
5.3. Найдите собственные векторы и собственные значения матрицы:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
.
5.4. При
каком значении параметра
![]() матрица
матрица
 имеет собственный вектор
имеет собственный вектор
![]() ,
соответствующий собственному значению
,
соответствующий собственному значению
![]() ?
?
5.5. При каком значении параметра матрица имеет собственный вектор , соответствующий собственному значению ?
5.7.
Проверьте,
что вектор
![]() является собственным вектором матрицы
является собственным вектором матрицы
![]() и найдите соответствующее ему собственное
значение
и найдите соответствующее ему собственное
значение
![]() :
:
 ,
,
 .
.
5.8. Проверьте, что вектор является собственным вектором матрицы и найдите соответствующее ему собственное значение .: , .
Ответы: 5.2. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
5.3. а)
.
5.3. а)
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ;
б)
;
б)
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
в)
;
в)
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
г)
;
г)
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
5.4.
![]() .
5.5.
.
5.5.
![]() .
5.7.
.
5.7.
![]() .5.8.
.5.8.
![]() .
.
6. Предел последовательности.
Вычислите пределы:
6.1
 ;
6.2
;
6.2
 ;
;
6.22
![]() ;
6.23
;
6.23
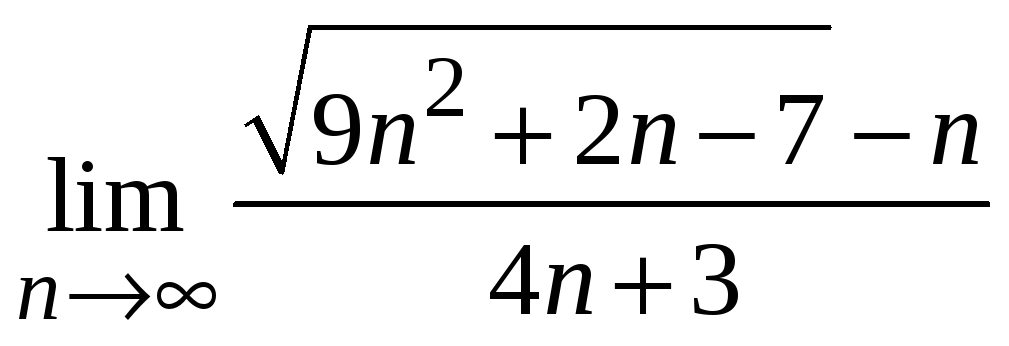 ;
;
6.27
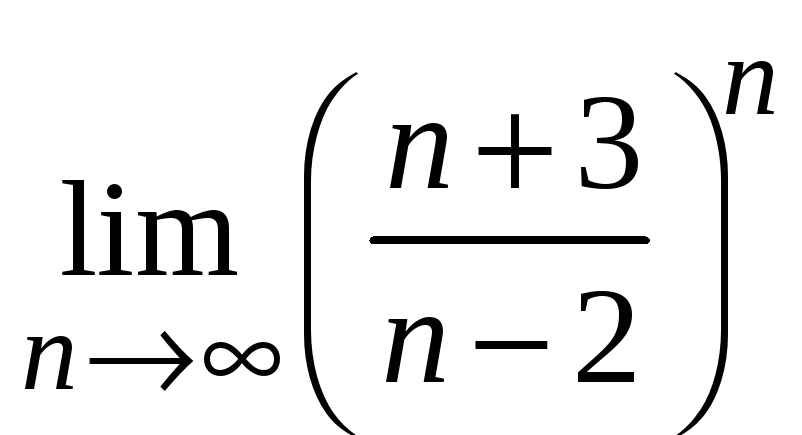 ;
6.28
;
6.28
 ;
6.29
;
6.29
![]() ;
;
Ответы: 6.1
![]() ;
6.2
;
6.2
![]() ;
6.22
;
6.22
![]() ;
6.23
;
6.23
![]() ;
6.27
;
6.27
![]() ;6.28
;6.28
![]() ;
6.29
;
6.29
![]() ;
;
7. Предел функции.
7.1 Вычислите пределы
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
 ;
з)
;
з)
 ;
;
7.3 Вычислите пределы, используя замены на эквивалентные
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
 ;
г)
;
г)
![]() ;
;
д)
 ;
е)
;
е)
 ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() ;
;
и)
 ;
к)
;
к)
 ;
л)
;
л)
![]() ;
м)
;
м)
![]() ;
н)
;
н)
![]() ;
;
о)
 ;
п)
;
п)
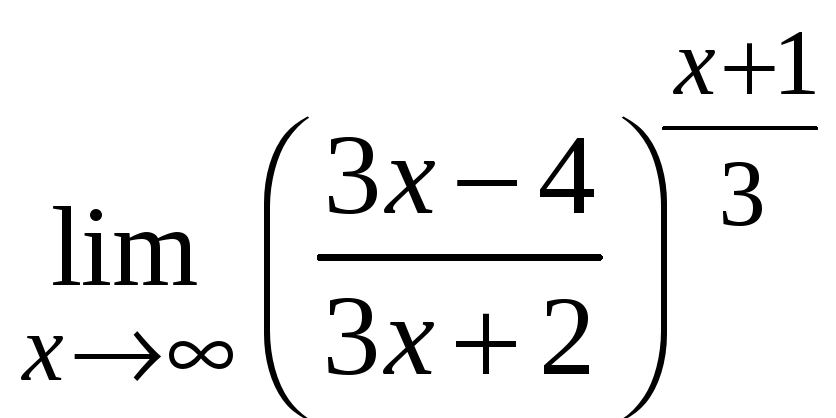 ;
р)
;
р)
 ;
с)
;
с)
 ;
;
т)
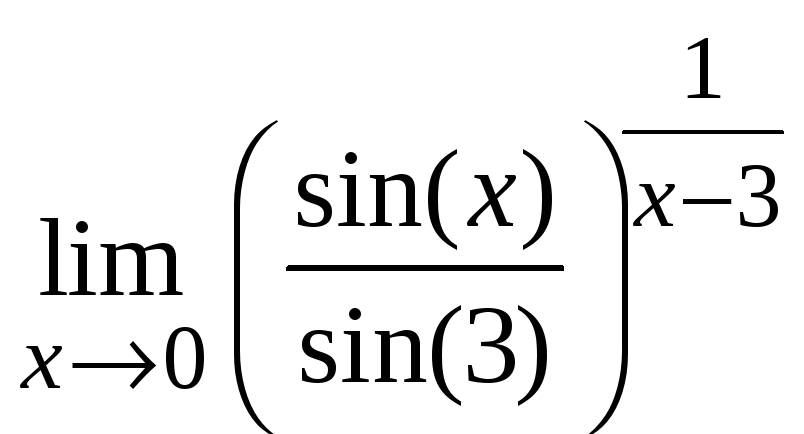 ;
у)
;
у)
 ;
ф)
;
ф)
 ;
;
x)
 ;
ц)
;
ц)
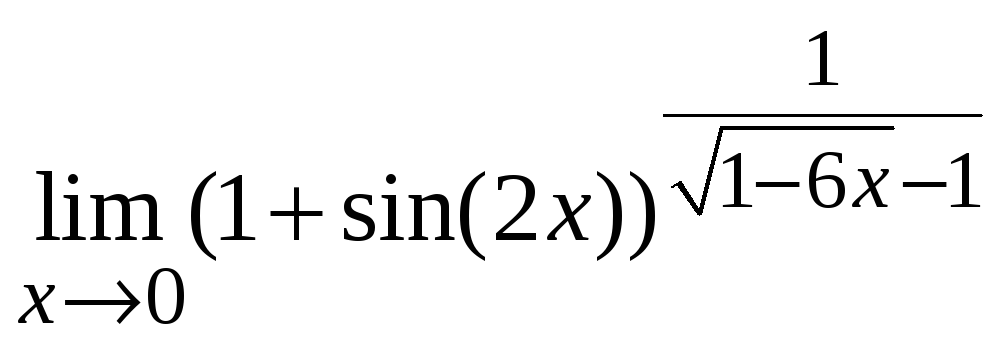 .
.
Ответы: 7.1 а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() :
г)
:
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() ;
и)
;
и)
![]() ;
к)
;
к)
![]() ;
л)
;
л)
![]() ;
м)
;
м)
![]() .
7.3 а)
.
7.3 а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;е)
;е)
![]() ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() ;
и)
;
и)
![]() ;
к)
;
к)
![]() ;
л)
;
л)
![]() ;
м)
;
м)
![]() ;
н)
;
н)
![]() ;
о)
;
о)
![]() ;
п)
;
п)
![]() ;
р)
;
р)
![]() ;
с)
;
с)
![]() ;
т)
;
т)
![]() ;
у)
;
у)
![]() ;
ф)
;
ф)
![]() ;
х)
;
х)
![]() ;
ц)
;
ц)
![]() .
.
8. Производная функции
Напишите уравнение
касательной к графику функции, заданной
параметрически, в точке, соответствующей
![]() :
:
8.22
![]() ,
,
![]() ,
,
![]() ;
8.23
;
8.23
![]() ,
,
![]() ,
,
![]() ;
;
8.30 Напишите
уравнение касательной, проведенной в
точке (1;1) к графику функции
![]() ,
заданной неявно
,
заданной неявно
![]() .
.
8.31 Напишите
уравнение касательной, проведенной в
точке (2;1) к графику функции
![]() ,
заданной неявно
,
заданной неявно
![]() .
.
8.33 Напишите
уравнение нормали, проведенной в точке
M(2;1)
к графику функции
![]() ,
заданной неявно
,
заданной неявно
![]() .
.
8.35 Напишите
уравнение нормали, проведенной в точке
M(1;1)
к графику функции
![]() ,
заданной неявно
,
заданной неявно
![]() .
.
Ответы: 8.22
![]() ;
8.23
;
8.23
![]() ;
8.30
;
8.30
![]() ;
8.31
;
8.31
![]() ;
;
8.33
![]() ;
8.35
;
8.35
![]() ;
;
