7. Метод вариации произвольных постоянных. Уравнение эйлера. Линейные дифференциальные уравнения с переменными коэффициентами

Метод вариации постоянныx применим для любого вида неодно-родных линейныx уравнений независимо от вида правой части и позволяет найти общее решение неоднородного уравнения во всех случаях, когда известно общее решение соответствующего однородного уравнения.

Пусть дифференциальное уравнение имеет вид:

, (7.1)

а общее решение соответствующего однородного уравнения:

где ФСР (7.1).

Общее решение неоднородного уравнения (7.1) будем искать в виде

(7.2)

где - неизвестные функции, которые определя-ются из следующей системы уравнений:

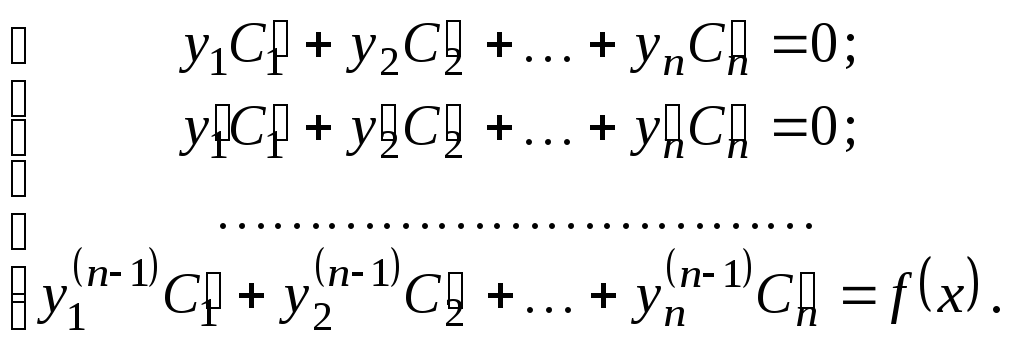
Система уравнений имеет единственное решение, так как её определитель (определитель Вронского)

.

Решая систему относительно , , получаем

,

откуда

, ,

где - произвольные постоянные.

Подставив найденные функции в уравнение (7.2), получим общее решение исходного неоднородного уравнения (7.1).

Для уравнения второго порядка

(7.3)

система уравнений имеет вид:

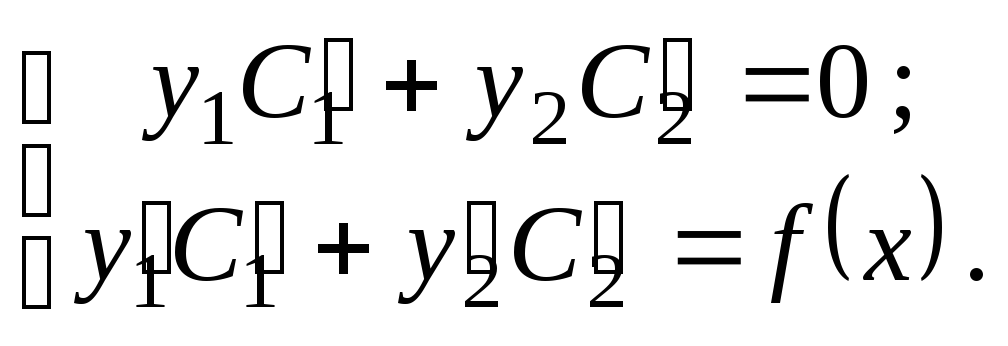
Решая её относительно неизвестных и , получим

, ,

откуда находим

,

подставив которые в уравнение , получим общее реше-ние уравнения (7.3).

Пример 7.1. .

Решение. Имеем однородное уравнение - , его характе-ристическое уравнение , корни , общее решение однородного уравнения:

Общее решение исходного неоднородного уравнения ищем в виде

, (7.4)

где и - неизвестные функции.

Система уравнений для их нахождения имеет вид:

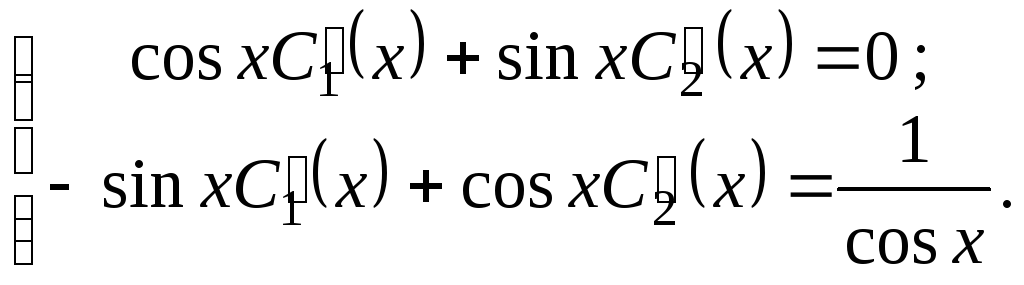
Определитель системы .

Система уравнений имеет единственное решение Интегрированием находим

Подставив последние выражения в уравнение (7.4), получаем общее решение исходного неоднородного уравнения:

причем - частное решение исходного урав-нения, .

Уравнение Эйлера. Уравнение вида

, (7.5)

где - постоянные, называется уравнением Эйлера. Оно приводится к линейному уравнению с постоянными коэффициентами подстановкой . Считая промежуточным аргументом, найдем производные:

и т.д.

Подстановка производных в уравнение Эйлера превращает его в уравнение с постоянными коэффициентами.

Пример 7.2. .

Решение. Полагая и подставив найденные выше выражения для производных, получим

или

.

Его характеристическое уравнение , корни .

Общее решение

,

или

.

Заметим, что вид решений уравнения Эйлера , или в исходных переменных . Поэтому можно искать решения в виде , не производя предварительно замену переменной .

Пример 7.3. .

Решение ищем в виде . Подставив это в уравнение, получим

,

или . Корни уравнения Общее реше-ние:

.

Здесь очевидно, что корню кратности соответствуют решений

а паре комплексно-сопряженных корней - пара решений

и .

Неоднородное уравнение Эйлера может быть проинтегрировано методом вариации произвольных постоянных. Для некоторых типов правых частей возможно применение метода неопределенных коэффи-циентов.

Линейные уравнения с переменными коэффициентами. Если известно частное решение линейного однородного уравнения вида

,(7.6)

то его порядок можно понизить на единицу при помощи подстановки

(7.7)

где - новая искомая функция. Полученное в результате уравнение также будет линейным.

Пример 7.4. Доказать, что если - частное решение линейного однородного уравнения второго порядка

, (7.8)

то второе его решение, линейно независимое с первым, находится по формуле:

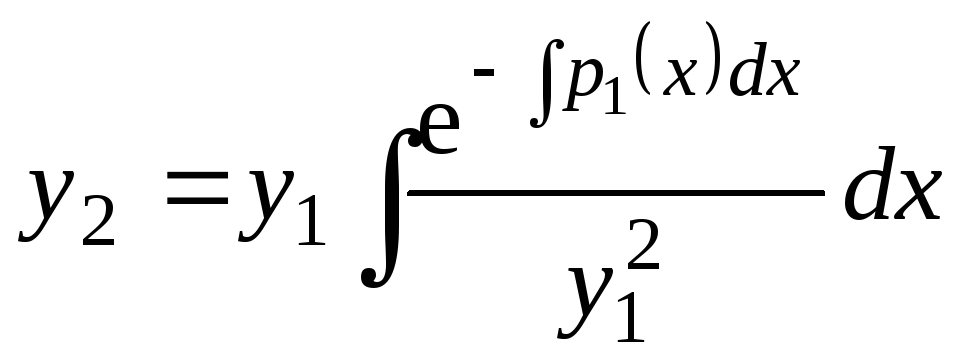. (7.9)

Решение. Подставим выражение (7.7) в уравнение (7.8), имея в виду, что . Получим

Подставив в уравнение (7.8), найдем

Выражение, стоящее в первых квадратных скобках, есть результат подста-новки решения в исходное уравнение, следовательно, равно нулю. Полученное уравнение

(7.10)

есть линейное однородное первого порядка.

Разделяя переменные, получим

.

Проинтегрируем

.

Откуда

Это - решение уравнения (7.10). Подставив в формулу (7.7), найдем второе решение уравнения (7.8)

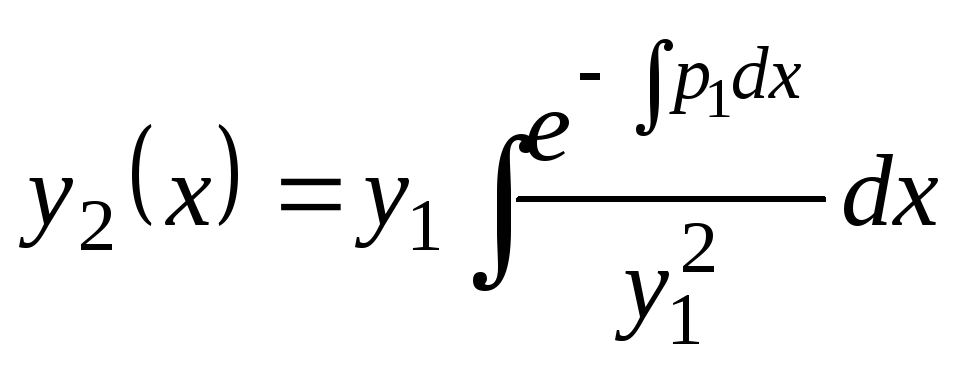. (7.11)

Это - формула Остроградского - Лиувилля для уравнения (7.8).

Пример 7.5.

Найти общее решение уравнения, если известно его частное решение

Решение. Здесь Вычислим входящий в формулу (7.11) интеграл

Далее

.

Подставив все в формулу (7.11), получим решение .

Общее решение уравнения:

Б. 4281.

.

Решение. Для нахождения общего решения этого неоднородного уравнения применим метод вариации произвольных постоянных.

Общее решение однородного уравнения имеет вид

Решение неоднородного уравнения будем искать в виде

. (7.12)

Неизвестные функции и определим из системы уравнений:

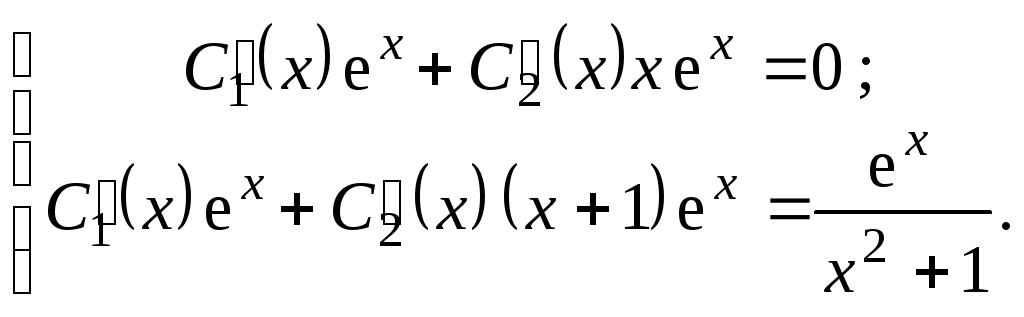
Вычитая первое уравнение из второго, находим

откуда

Подставив в первое уравнение, получим

Подставив и в выражение (7.12), получим общее решение неоднородного уравнения

где .

Б. 4289.

.

Решение. Это - уравнение Эйлера. Решение ищем в виде . Подставив в уравнение, получим откуда - характеристическое уравнение. Корни его , Общее решение

Б. 4242.

Решение. Однородное уравнение имеет решение , в чем легко убедиться, подставив его в уравнение. Решение найдем по формуле Остроградского - Лиувилля (7.11), учитывая, что

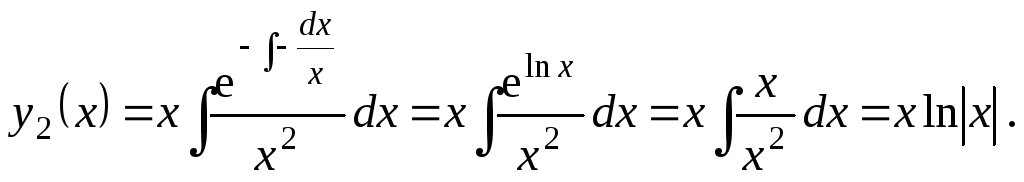
Общее решение однородного уравнения:

.

Общее решение неоднородного уравнения найдем методом вариации про-извольных постоянных в виде

. (7.13)

Система уравнений для неизвестных функций и :

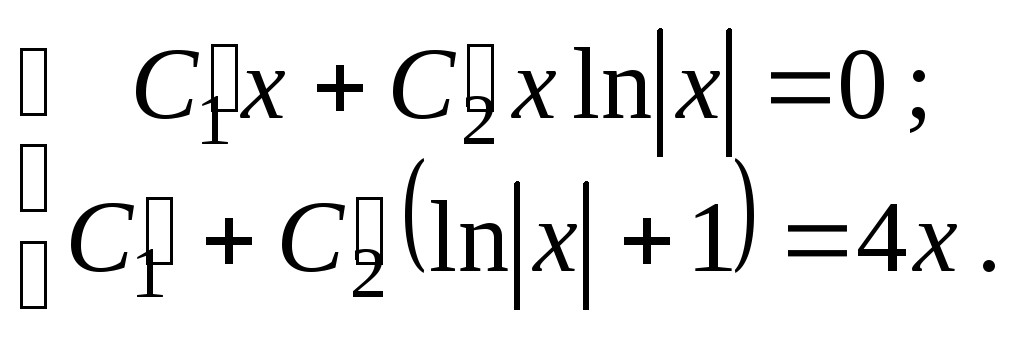
Умножив второе уравнение на x и вычтя из него первое, получим

Подставив в первое уравнение , найдем

,

откуда

Подставив и в формулу (7.13), получим общее решение

,

или

Составление дифференциального уравнения по заданной фунда-ментальной системе решений.

Пусть - линейно независимые n раз диффе-ренцируемые функции. Тогда уравнение:

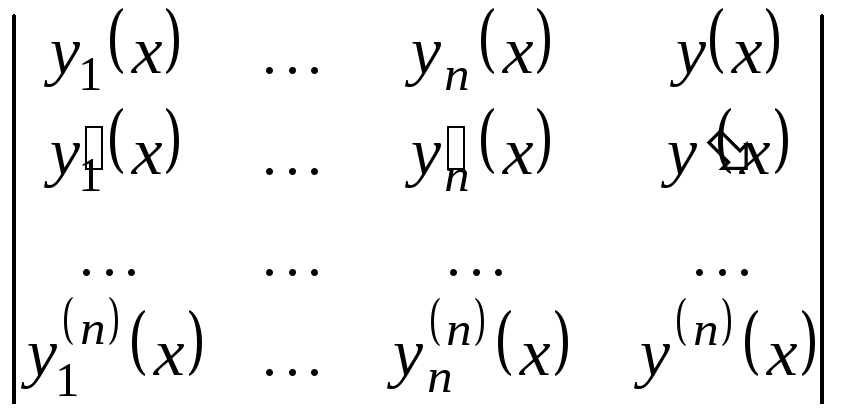= 0, (14)

где - неизвестная функция, будет линейным дифференциальным уравнением, для которого функции образуют фундамен-тальную систему решений.

Пример 7.6. Составить дифференциальное уравнение, для которого и образуют фундаментальную систему решений.

Решение. Составим определитель (7.14).

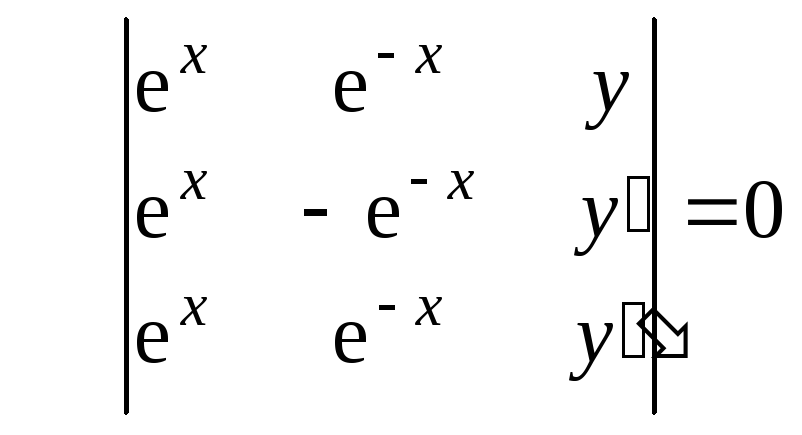или .

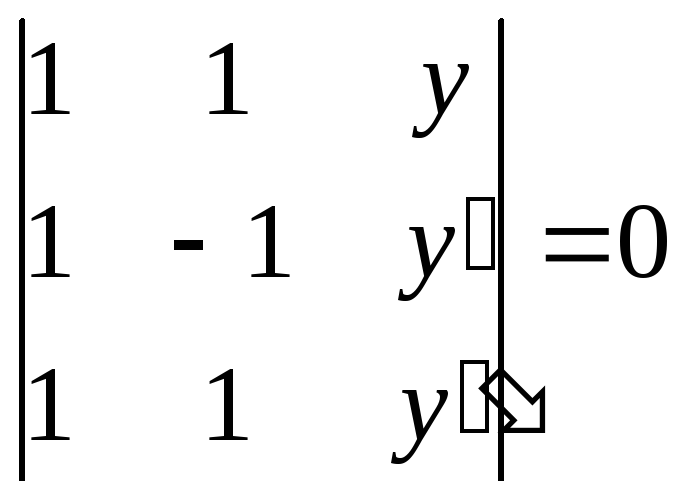Раскрывая определитель по элементам третьего столбца, получим искомое дифференциальное уравнение .

Б. 4230. Составить дифференциальное уравнение, для которого функ-ции и образуют фундаментальную систему решений.

Решение. Составим определитель (7.14)

.

Раскроем его по элементам третьего столбца.

.

Вычислив определители второго порядка и отбросив общий множитель , получим

Решить самостоятельно Б. 4228, Б. 4238, Б. 4240, Б. 4243, Б. 4280, Б. 4282, Б. 4290, Б. 4291.