Регрессия Линейная регрессия

Для нахождения коэффициентов A и B методом наименьших квадратов были посчитаны следующие необходимые параметры:

= 11473,89;

= 919,47;

= 37342,92;

= 3082,16.

В нашем случае коэффициенты A и B соответственно равны:

A = 2,98; B = 3,40.

Следовательно, график линейной регрессии для нашей выборки имеет вид:

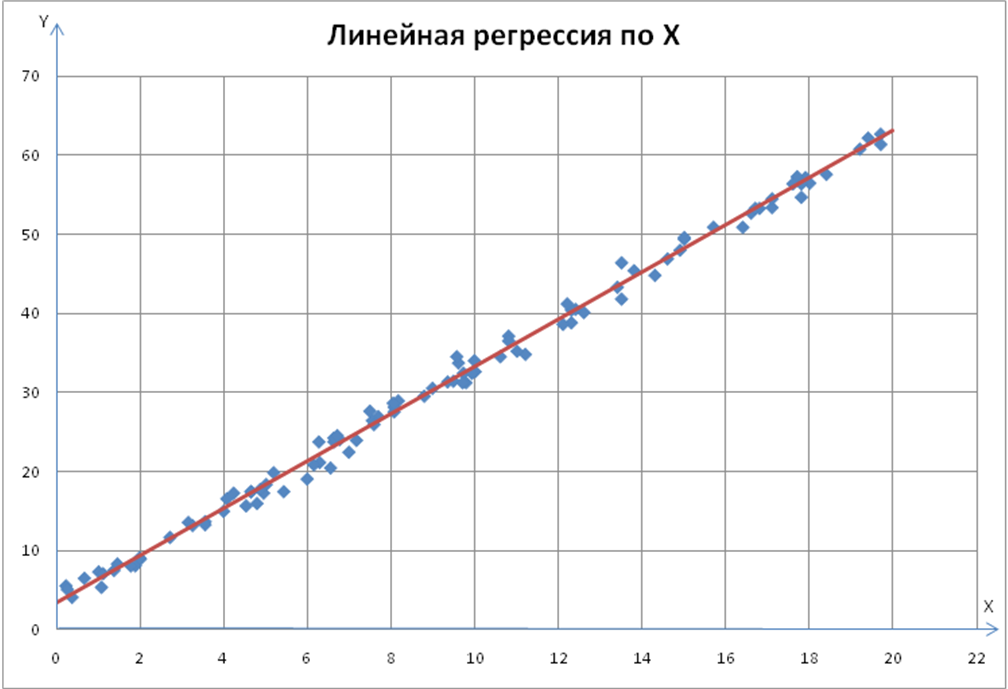
Рис. 12. Линейная регрессия по Х

Найдем параметры C и D, подставив вычисленные по таблице суммы в полученные формулы:

Получим график линейной регрессии:

Рис. 12а. Линейная регрессия по Y

Параболическая регрессия

Для нахождения коэффициентов a, b и c методом наименьших квадратов были посчитаны следующие необходимые параметры:

В нашем случае коэффициенты p, q и r соответственно равны:

p = 0, 01; q = 2, 98; r = 3, 47.

Следовательно, график параболической регрессии для нашей выборки имеет вид:

Рис. 13. Параболическая регрессия

Проанализируем полученные нами уравнения регрессий. Для этого найдём среднеквадратические отклонения полученных регрессий по формулам:

Указанная формула используется для линейной и параболической регрессий, затем сравнивают полученные результаты и находят наименьшие. Та регрессия, у которой будут наименьшая оценка, более точно отражает распределение точек на диаграмме рассеивания.

Сначала посчитаем оценку для линейной регрессии:

А теперь для параболической:

Из подсчетов видно, что суммарное отклонение линейной регрессии больше, чем суммарное отклонение параболической регрессии, следовательно, параболическая регрессия точнее отражает функциональную зависимость X от Y.

Индекс выпуска товаров и услуг Исходные данные и их обработка

Индекс выпуска товаров и услуг по базовым видам экономической деятельности исчисляется на основе данных об изменении физического объема производства продукции сельского хозяйства, добычи полезных ископаемых, обрабатывающих производств, производства и распределения электроэнергии, газа и воды, строительства, транспорта, розничной и оптовой торговли. Данные были взяты с сайта Федеральной службы государственной статистики, Банк России. Рассмотрим зависимость индекса выпуска товаров и услуг от времени за период с 2006 по 2010 года с интервалом в один месяц.

Дата	Индекс	Дата	Индекс	Дата	Индекс	Дата	Индекс	Дата	Индекс
янв.06	106,2	ноя.06	109,6	сен.07	104,5	июл.08	104,8	май.09	85
фев.06	104,5	дек.06	109,4	окт.07	107,4	авг.08	105,5	июн.09	87,2
мар.06	108,1	янв.07	107,1	ноя.07	106,5	сен.08	106,1	июл.09	89,5
апр.06	107,4	фев.07	105,6	дек.07	107,7	окт.08	102,6	авг.09	88,8
май.06	111,5	мар.07	106,4	янв.08	107,8	ноя.08	95,8	сен.09	91,5
июн.06	108,1	апр.07	106,1	фев.08	110,7	дек.08	93,2	окт.09	93,4
июл.06	108,2	май.07	106,7	мар.08	108,9	янв.09	86	ноя.09	104,9
авг.06	109,4	июн.07	108,9	апр.08	109,6	фев.09	85,5	дек.09	101,9
сен.06	109,4	июл.07	110	май.08	107,3	мар.09	87,1	янв.10	104,1
окт.06	110,4	авг.07	105,2	июн.08	104,1	апр.09	85,9	фев.10	104,1

На основе данных, приведенных выше, построим диаграмму рассеивания и график линейной регрессии, у которого по расчетам А = 0,37; В = 112,19:

Р

Изучив график, можно спрогнозировать, что в ближайшие месяцы индекс выпуска товаров и услуг будет уменьшаться.

ис. 14. Диаграмма рассеивания