
Международный университет природы, общества и человека «Дубна»
Кафедра распределенных информационно-вычислительных систем
Кафедра высшей математики
Курсовая работа
по теории вероятностей и математической статистике
«Изучение характера зависимости между признаками X и Y»
Выполнила:
студентка II курса
группы 2201
Эпштейн М.А.
Руководители:
доцент
Калиновская Л.В.
доцент
Мурадян А.В.
Дубна, 2010
Оглавление
Оглавление 2
Введение 3
Постановка задачи 4
Исходные данные и их обработка 8
Корреляционный анализ 9
Регрессия 15
Линейная регрессия 15
17
Параболическая регрессия 17
Индекс выпуска товаров и услуг 19
Исходные данные и их обработка 19
Заключение 20
Список литературы 21
Введение
Математическая статистика — наука о математических методах систематизации и использовании статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надёжность и точность выводов, делаемых на основании ограниченного статистического материала (выборки).
Во время статистических наблюдений для каждого объекта в ряде случаев можно измерить значение нескольких признаков. Таким образом, получается многомерная выборка. Если многомерную выборку обработать по значениям отдельного признака, то получится обычная обработка одномерной выборки.
Смысл обработки многомерных выборок состоит в том, чтобы установить связь между признаками. Связи могу быть функциональными, то есть каждому значению одной величины соответствует определенное значение другой величины.
Связь между случайными величинами часто носит случайный характер и называется статистической, если изменение одной величины вызывает изменение распределения другой величины. Если среднее значение одной случайной величины функционально зависит от значения другой случайной величины, то такая статистическая зависимость называется корреляционной.
Постановка задачи
Даны выборки
![]() .
.
![]() ,
,
![]() — значения двух признаков исследуемого
объекта.
— значения двух признаков исследуемого
объекта.
Требуется:
-
Изобразить точки
 на диаграмме рассеивания. Построить
корреляционную таблицу. Найти все
выборочные числовые параметры:
на диаграмме рассеивания. Построить
корреляционную таблицу. Найти все
выборочные числовые параметры:
 ,
моду и медиану выборки по
,
моду и медиану выборки по
 и
по
и
по
 ,
выборочный коэффициент корреляции
,
выборочный коэффициент корреляции
 .
Построить гистограммы
.
Построить гистограммы
 и
и
 по
корреляционной таблице.
по
корреляционной таблице. -
Определить числа
 и
и
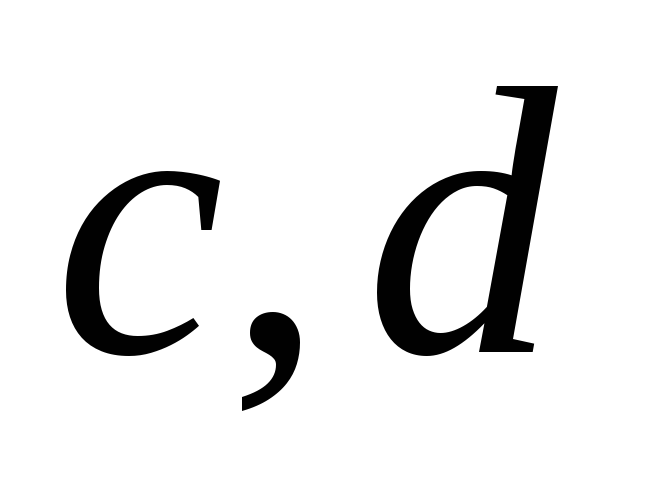 ,
такие, чтобы уравнения линейных регрессий
,
такие, чтобы уравнения линейных регрессий
 и
и
 наименее отклонялись от экспериментальных
данных. Найти выборочный коэффициент
регрессии
наименее отклонялись от экспериментальных
данных. Найти выборочный коэффициент
регрессии
 .
Изобразить обе линии регрессии на
диаграмме рассеивания.
.
Изобразить обе линии регрессии на
диаграмме рассеивания.
-
Определить числа
 такие, чтобы линия квадратичной регрессии
такие, чтобы линия квадратичной регрессии
 наименее отклонялась от экспериментальных
данных. Построить графики параболической
регрессий на диаграмме рассеивания.
наименее отклонялась от экспериментальных
данных. Построить графики параболической
регрессий на диаграмме рассеивания. -
Сравнить между собой результаты пунктов 2 и 3 и ответить на вопрос задания о наличии и виде зависимости между признаками
 и
и
 .
. -
Найти 50 чисел, показывающих зависимость чего-либо от времени, построить диаграмму рассеивания и линейную регрессии, а также сделать прогноз на
ближайшее время.
Теоретическая часть
Приведем основные понятия и определения из курса теории вероятности и математической статистики, которые будут иметь место в данной работе.
Теория вероятностей — математическая наука, изучающая закономерности в случайных явлениях.
Математическая статистика — наука, в задачи которой входит разработка методов для сбора, обработки и анализа данных и их интерпретация, позволяющая проникнуть в структуру массовых явлений.
Генеральная совокупность — совокупность объектов, из которых производится случайный выбор объектов для исследования.
Выборочная совокупность — отобранные случайным образом объекты из генеральной совокупности.
Объем генеральной (выборочной) совокупности — число объектов совокупности.
Относительная частота — отношение числа наблюдений к объему выборки.
Диаграмма рассеивания (корреляционное
поле) — график в ДПСК, на котором
откладываются все пары точек
![]() .
.
Гистограмма относительных частот
— ступенчатая фигура, состоящая из
прямоугольников, основанием которых
служит интервал длины
![]() ,
а высоты равны
,
а высоты равны
![]() .
.
Выборочное среднее — среднее
арифметическое значений вариант выборки
![]() .
.
Выборочная дисперсия — среднее
арифметическое квадрата отклонения
случайных величин от их среднего значения
![]() .
Исправленная дисперсия
.
Исправленная дисперсия
![]() .
.
Мода выборки — варианта с наибольшей частотой.
Медиана выборки — серединное значение выборки.
Ковариация (корреляционный момент)
двух случайных величин
![]() и
и
![]() — это математическое ожидание произведения
отклонений случайных величин от их
математического ожидания
— это математическое ожидание произведения
отклонений случайных величин от их
математического ожидания
![]() .
.
Коэффициентом корреляции двух
случайных величин заданных на одном
вероятностном пространстве называется
величина
![]() .
.
Если для двух случайных величин
![]() и
и
![]() можно хотя бы приближенно записать, что
можно хотя бы приближенно записать, что
![]()
![]() ,
то говорят, что
,
то говорят, что
![]() и
и
![]() связаны линейной (квадратичной)
корреляцией.
связаны линейной (квадратичной)
корреляцией.
Корреляция — это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
Коэффициентом корреляции
![]() случайных величин X и Y называют
отношение корреляционного момента к
произведению средних квадратичных
отклонений этих величин:
случайных величин X и Y называют
отношение корреляционного момента к
произведению средних квадратичных
отклонений этих величин:
![]() ,
причем
,
причем
![]() . (1)
. (1)
Из формулы (1) видно, что для независимых случайных величин коэффициент корреляции равен нулю, так как для таких величин Kxy = 0.
Случайные величины, для которых
![]() =
0, называют некоррелированными
(несвязанными).
=
0, называют некоррелированными
(несвязанными).
Отметим, однако, что из некоррелированности случайных величин не следует их независимость.
Коэффициент корреляции характеризует не всякую зависимость, а только так называемую линейную зависимость. Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или же убывать) по линейному закону. Таким образом, коэффициент корреляции характеризует степень тесноты линейной зависимости между случайными величинами.
Рассчитаем коэффициент
![]() ,
,
где Kxy
— ковариация,
![]() и
и
![]() — средние квадратичные отклонения
случайных величин.
— средние квадратичные отклонения
случайных величин.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Дисперсия случайной величины есть характеристика рассеивания, разбросанности значений случайной величины около её математического ожидания. Само слово «дисперсия» означает «рассеивание».
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Итак, если
![]() =
0, то X и Y
— независимые случайные величины; если
=
0, то X и Y
— независимые случайные величины; если
![]() =
=
![]() 1,
то это строгая функциональная зависимость;
+1 — возрастающая регрессия, –1 —
убывающая регрессия.
1,
то это строгая функциональная зависимость;
+1 — возрастающая регрессия, –1 —
убывающая регрессия.
Коэффициенты корреляции, представляя
количественную характеристику тесноты
связи между признаками, служат также
оценкой соответствия уравнения регрессии
выявленным причинно-следственным
связям. Для исследуемой взаимосвязи
между X и Y, коэффициент корреляции
![]() =
0,98.
=
0,98.
Полученное значение коэффициента корреляции характеризует прямую связь между исследуемыми величинами, т.к. оно положительно.
.
