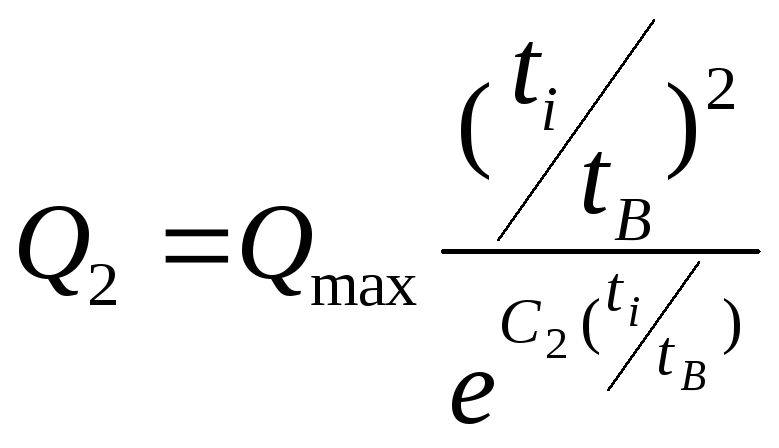Висновок
На рисунку 1.1 зображені S-подібна крива і зв'язок S-подібної кривої з питомими матеріалоємністю, трудомісткістю і собівартістю технічної системи для варіанта «Приклад». На графіках видно, що на початку бурхливого розвитку технічної системи (кр. В) значення питомих матеріалоємності, трудомісткості і собівартості дорівнюють одиниці і по мірі розвитку технічної системи значення питомих матеріалоємності, трудомісткості і собівартості зменшуються, причому значення питомої матеріалоємності зменшуються найбільше і до кінця життєвого циклу даної технічної системи має значення 0,28, питомої трудомісткості – 0,44, а питомої собівартості - 0,64.
Практична робота 2
Визначення характеристик винахідницької діяльності
Ціль: закріплення лекційного і навчального матеріалу, що стосується характеристик винахідницької діяльності.
1 Зв'язок винахідницької діяльності з розвитком технічних систем
Винахідник Альтшуллер Г.С. звернув увагу на деякі статистичні закономірності, що пов'язують S-подібну криву з рівнем винаходів, їхньою кількістю і величиною отримуємого прибутку на різних етапах розвитку технічних систем. Ці закономірності в графічній формі представлені на рисунку 2.1.
Рисунок 2.1 – Зв’язок S-подібної кривої з характерис-тиками винахідницької діяльності
Коли виникає ідея нової технічної системи, то це характеризується самим високим рівнем винаходу (рис. 2.1, а; б). За цим першим винаходом виникають менш значні винаходи, що стосуються удосконалення цієї технічної системи.
В міру освоєння нової технічної системи рівень наступних винаходів неухильно падає, трохи піднімаючись лише при переході до масового випуску даної технічної системи (крапка В на S-подібній кривій).
Кількість винаходів навпаки має тенденцію до зростання (рис. 2.1, в). При цьому спостерігається два піки на кривій. Перший пік збігається за часом із крапкою В на S-подібній кривій, другий пік - із крапкою D, коли технічна система цілком вичерпує можливості фізичного принципу, що лежить у її основі. Наявність другого піка можна пояснити прагненням «вичавити» з технічної системи все можливе. Оскільки до часу tD технічна система вже добре вивчена й освоєна багатьма фахівцями, то і кількість винаходів виходить значною.
Прибуток від нової технічної системи в початковий період (від t0 до tВ) негативний, тому що мають місце тільки витрати (рис. 2.1, г). Прибуток з'являється після початку масового випуску нової технічної системи, він інтенсивно росте в міру удосконалювання технічної системи і починає сповільнюватися в міру вичерпання фізичного принципу, закладеного в неї.
2 Розрахунки характеристик винахідницької діяльності
Усі характеристики винахідницької діяльності мають подібну методику визначення. Необхідно знати граничні значення параметрів (рівня винаходу Q, кількість винаходів N і прибутку C), а також час tВ і tD. Використовуючи ці значення, визначають характерні константи експонент.
Після цього проводяться розрахунки по апроксимуючим формулам і будуються графіки Q=f1(t), N=f2(t) і C=f3(t).
2.1 Рівень винаходів
Рівень винаходів може бути аппроксимирован вираженням виду:
. (2.1)
Коефіцієнти при експонентах:
, (2.2)
. (2.3)
Вираження (2.1) описує криву Qmax, показану на рис. 2.1, б. Використовуючи таблицю вихідних даних свого варіанта обчислюють С1 і С2, користаючись вираженнями (2.2) і (2.3).
Для розглянутого варіанта «Приклад» рівень винаходів в характерних крапках кривої буде дорівнювати: Qmax =10 балів, QB =1,08 бала, QD = 2,35 бала. tD = 16 років, tB = 0,25• tD = 0,25• 16 = 4роки.
1,45,
2,225.
За результатами обчислень знайшли коефіцієнти при експонентах: С1 = 1,45; С2 = 2,225. Обчислення проводимо в таблицях 2.1 і 2.2. За даними останніх стовпчиків цих таблиць складаємо таблицю 2.3. Таблиця 2.1 є результатом першого доданку, а таблиця 2.2 - другого доданку вираження (2.1), тобто вважаємо, що вираження (2.1) можна записати як суму двох доданків:
,
де
, 
(2.4)
. (2.5)
За даними останнього рядка таблиці 2.3 будуємо графік Q=f1(t), рис. 2.2.
Таблиця 2.1- Розрахунок по вираженню (2.4)
|
ti |
ti/tD |
|
|
|
|
|
0 |
0,00 |
0,00 |
1,00 |
1,00 |
10,0 |
|
1 |
0,06 |
0,087 |
1,09 |
0,92 |
9,2 |
|
2 |
0,13 |
0,188 |
1,21 |
0,83 |
8,3 |
|
3 |
0,19 |
0,275 |
1,32 |
0,76 |
7,6 |
|
4 |
0,25 |
0,36 |
1,44 |
0,69 |
6,9 |
|
5 |
0,31 |
0,45 |
1,57 |
0,64 |
6,4 |
|
6 |
0,38 |
0,55 |
1,73 |
0,58 |
5,8 |
|
7 |
0,44 |
0,64 |
1,89 |
0,53 |
5,3 |
|
8 |
0,50 |
0,725 |
2,06 |
0,48 |
4,8 |
|
12 |
0,75 |
1,09 |
2,97 |
0,34 |
3,4 |
|
16 |
1,00 |
1,45 |
4,26 |
0,23 |
2,3 |
|
20 |
1,25 |
1,81 |
6,13 |
0,16 |
1,6 |
Таблиця 2.2 – Розрахунок по вираженню (2.5)
|
ti |
ti/tB |
|
|
(ti/tB)2 |
|
|
|
0 |
0,00 |
0,00 |
1,00 |
0,00 |
0,00 |
0,0 |
|
1 |
0,25 |
0,57 |
1,74 |
0,06 |
0,034 |
0,34 |
|
2 |
0,50 |
1,11 |
3,04 |
0,25 |
0,082 |
0,82 |
|
3 |
0,75 |
1,67 |
5,3 |
0,56 |
0,1 |
1,06 |
|
4 |
1,00 |
2,30 |
9,97 |
1,00 |
0,10 |
1,0 |
|
5 |
1,25 |
2,81 |
16,65 |
1,56 |
0,094 |
0,94 |
|
6 |
1,50 |
3,375 |
29,2 |
2,25 |
0,077 |
0,77 |
|
7 |
1,75 |
3,89 |
49,1 |
3,06 |
0,062 |
0,62 |
|
8 |
2,00 |
4,45 |
85,6 |
4,00 |
0,047 |
0,47 |
|
12 |
3,00 |
6,675 |
792,35 |
9,00 |
0,011 |
0,11 |
|
16 |
4,00 |
8,9 |
7332 |
16,00 |
0,0022 |
0,022 |
|
20 |
5,00 |
11,125 |
67846 |
25,00 |
0,00037 |
0,0037 |
Таблиця 2.3 – Розрахунок по вираженню (2.1)
|
ti |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
12 |
16 |
20 |
|
Q1 |
10,0 |
9,2 |
8,3 |
7,6 |
6,9 |
6,4 |
5,8 |
5,3 |
4,8 |
3,4 |
2,3 |
1,6 |
|
Q2 |
0,0 |
0,34 |
0,82 |
1,06 |
1,0 |
0,94 |
0,77 |
0,62 |
0,47 |
0,11 |
0,02 |
0,0 |
|
Q |
10,0 |
9,54 |
9,12 |
8,66 |
7,9 |
7,34 |
6,57 |
5,92 |
5,27 |
3,51 |
2,32 |
1,6 |
Рисунок 2.2 – Приклад побудова кривої рівня винаходів Q=f1(t)